Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску
Гамильтоново разложение Валецкого полного графа

В теории графов, разделе математики, гамильтоново разложение данного графа - это разбиение ребер графа на гамильтоновы циклы . Гамильтоновы разложения изучались как для неориентированных, так и для ориентированных графов ; в неориентированном случае гамильтоново разложение можно также описать как 2-факторизацию графа, при которой каждый фактор связан.

Необходимые условия [ править ]

Чтобы гамильтоново разложение существовало в неориентированном графе, граф должен быть связным и регулярным четной степени . Ориентированный граф с таким разбиением должен быть сильно связным, и все вершины должны иметь одинаковую внутреннюю и исходящую степени, но эта степень не обязательно должна быть четной. [1]

Медиальный график , на графике Гершеля является 4-регулярным плоским графом , без гамильтоново разложения. Заштрихованные области соответствуют вершинам нижележащего графа Гершеля.

Для 4-регулярных плоских графов дополнительные необходимые условия могут быть получены из теоремы Гринберга . Пример 4-регулярного плоский граф , который не соответствует этим условиям, и не имеет гамильтон разложения, задаются медиальным графом из графа Гершеля . [2]

Полные графики [ править ]

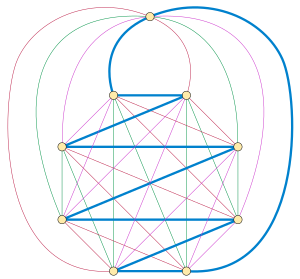
Каждый полный граф с нечетным числом вершин имеет гамильтоново разложение. Этот результат, который является частным случаем задачи Обервольфаха о разложении полных графов на изоморфные 2-факторы, был приписан Валецкому Эдуардом Лукасом в 1892 году. Конструкция Валецки помещает вершины в правильный многоугольник и покрывает в нем полный граф. подмножество вершин с гамильтоновыми путями, которые зигзагообразно пересекают многоугольник, причем каждый путь повернут относительно друг друга на величину, кратную . Затем все пути можно дополнить до гамильтоновых циклов, соединив их концы через оставшуюся вершину. [3]

Расширение вершины -регулярного графа в клики из вершин, по одному для каждой конечной точки ребра в замененной вершине, не может изменить , имеет ли граф гамильтон разложения. Обратный процесс расширения, сворачивание клики в одну вершину, преобразует любое гамильтоново разложение в большем графе в гамильтоново разложение в исходном графе. И наоборот, конструкция Валецки может быть применена к клике для расширения любого гамильтонова разложения меньшего графа в гамильтоново разложение расширенного графа. Этот процесс расширения может использоваться для создания произвольно больших вершинно-транзитивных графов и графов Кэли четной степени, не имеющих гамильтоновых разложений.[4]

Направленный случай полных графов - турниры . Отвечая на гипотезу Пола Келли от 1968 года, [5] Даниэла Кюн и Дерик Остхус доказали в 2012 году, что каждый достаточно большой регулярный турнир имеет гамильтоново разложение. [6]

Количество разложений [ править ]

Каждый 4-регулярный неориентированный граф имеет четное число гамильтоновых разложений. Более того, для любых двух ребер и 4-регулярного графа число гамильтоновых разложений, в которых и принадлежат одному и тому же циклу, четно. Если -регулярный граф имеет гамильтоново разложение, он имеет по крайней мере тройное факториальное число разложений,

Например, 4-регулярные графы с гамильтоновым разложением имеют по крайней мере четыре из них; 6-регулярные графы с гамильтоновым разложением имеют не менее 28 и т. Д. Отсюда следует, что единственными графами, гамильтоновы разложения которых уникальны, являются цикловые графы . [7]

Вычислительная сложность [ править ]

Проверка того, имеет ли произвольный граф гамильтоново разложение, является NP-полной как в направленном, так и в неориентированном случаях. [8]

На линейные графики из кубических графов являются 4-регулярным, и имеют гамильтонов разложение , если и только если основной кубический граф имеет гамильтонов цикл. [9] [10] Как следствие, гамильтоново разложение остается NP-полным для классов графов, которые включают линейные графы жестких примеров проблемы гамильтонова цикла . Например, гамильтоново разложение является NP-полным для 4-регулярных плоских графов, потому что они включают линейные графы кубических плоских графов. С другой стороны, эта эквивалентность также означает, что гамильтоново разложение легко для 4-регулярных линейных графов, когда лежащие в их основе кубические графы имеют простые проблемы с гамильтоновым циклом.

Случайные регулярные графы четной степени почти наверняка имеют гамильтоново разложение, и, что более важно, существует алгоритм рандомизированного полиномиального времени , который, будучи заданным в качестве входных данных случайным регулярным графом четной степени, почти наверняка находит в нем гамильтоново разложение. [11]

См. Также [ править ]

  • Линейная древовидность , другой вид ограниченного разбиения на подграфы максимальной степени два

Ссылки [ править ]

  1. ^ Бермонд, Ж.-К. (1978), "Гамильтоновы разбиения графов, ориентированных графов и гиперграфов" , Анналы дискретной математики , 3 : 21-28 , DOI : 10.1016 / S0167-5060 (08) 70494-1 , ISBN 9780720408430, Руководство по ремонту  0505807
  2. ^ Бонди, JA ; Häggkvist, R. (1981), "Край-непересекающиеся Гамильтон циклы в 4-регулярных плоских графов", Aequationes Mathematicae , 22 (1): 42-45, DOI : 10.1007 / BF02190157 , MR 0623315 
  3. ^ Alspach, Брайан (2008), "Чудесная строительство Валецки", Бюллетень Института комбинаторике и ее применения , 52 : 7-20, MR 2394738  CS1 maint: discouraged parameter (link)
  4. ^ Брайант, Даррин; Дин, Мэтью (2015), "Vertex-транзитивных графов , которые не имеют разложение Гамильтона", Журнал комбинаторной теории, Series B , 114 : 237-246, DOI : 10.1016 / j.jctb.2015.05.007 , МР 3354297 
  5. ↑ Moon, John W. (1968), Темы турниров , Нью-Йорк, Монреаль, Лондон: Холт, Райнхарт и Уинстон, Упражнение 9, стр. 9, MR 0256919 
  6. ^ Кюн, Даниэла ; Osthus, Deryk (2013), "Гамильтон разложение регулярных расширителей: доказательство гипотезы Келли для крупных турниров", достижений в области математики , 237 : 62-146, Arxiv : 1202,6219 , DOI : 10.1016 / j.aim.2013.01.005 , Руководство по ремонту 3028574 
  7. ^ Томасон, А. Г. (1978), "Гамильтоновы циклы и уникально края благовидных графов", Авансы в теории графов (Cambridge Комбинаторных Conf., Тринити - колледж, Кембридж, 1977) , Annals дискретной математики, 3 , стр. 259-268, MR 0499124 
  8. ^ Péroche, В. (1984), "NP-полнота некоторых задач разделения и покрытия в виде графиков", Дискретная прикладная математика , 8 (2): 195-208, DOI : 10.1016 / 0166-218X (84) 90101-X , Руководство по ремонту 0743024 
  9. ^ Коциг, Антон (1957), "Aus дер Теорье дер endlichen regulären графена dritten унд vierten сорта", Československá Akademie VEd , 82 : 76-92, МР 0090815  CS1 maint: discouraged parameter (link)
  10. ^ Мартин Пьер (1976), "Циклы hamiltoniens йапз ль-4 в виде графиков Регулирсдварсстраят 4-connexes", Aequationes Mathematicae , 14 (1/2): 37-40, DOI : 10.1007 / BF01836203 , МР 0414442 
  11. ^ Ким, Чон Хан; Вормальд, Николас К. (2001), «Случайные сопоставления, которые индуцируют гамильтоновы циклы и гамильтоновы разложения случайных регулярных графов», Журнал комбинаторной теории, серия B , 81 (1): 20–44, DOI : 10.1006 / jctb.2000.1991 , Руководство по ремонту 1809424