Парадокс Гильберта в Гранд Отеле

Эта статья включает в себя список общих ссылок , но он остается в основном непроверенным, поскольку в нем отсутствуют соответствующие встроенные ссылки . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Февраль 2016 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

Отель Гильберта

Парадокс Гильберта о Grand Hotel ( разговорном : Бесконечный Отель Paradox или отеле Гильберта ) является мысленным экспериментом , который иллюстрирует противоречащее свойство бесконечных множеств. Показано, что в полностью занятом отеле с бесконечно большим количеством номеров могут по-прежнему проживать дополнительные гости, даже бесконечно много, и этот процесс может повторяться бесконечно часто. Идея была представлена Дэвидом Гильбертом в лекции 1924 года «Über das Unendliche», перепечатанной в ( Hilbert 2013 , p.730), и была популяризирована в книге Джорджа Гамова 1947 года « Один, два, три ... бесконечность» . ^[1]^[2]

Парадокс [ править ]

Рассмотрим гипотетический отель со счетным бесконечным числом комнат, все из которых заняты. Может возникнуть соблазн подумать, что отель не сможет принять новых гостей, как это было бы в случае с ограниченным числом номеров, где будет применяться принцип « решетки».

Конечное количество новых гостей [ править ]

Предположим, прибывает новый гость и желает разместиться в отеле. Мы можем (одновременно) переместить гостя, который сейчас находится в комнате 1, в комнату 2, гостя, находящегося в настоящее время в комнате 2, в комнату 3 и так далее, перемещая каждого гостя из их текущей комнаты n в комнату n +1. После этого комната 1 пуста, и нового гостя можно переместить в эту комнату. Повторяя эту процедуру, можно освободить место для любого конечного числа новых гостей.

Бесконечно много новых гостей [ править ]

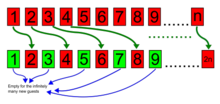
Также возможно разместить счетное бесконечное количество новых гостей: просто переместите человека, занимающего комнату 1, в комнату 2, гостя, занимающего комнату 2, в комнату 4, и, как правило, гостя, занимающего комнату n, в комнату 2 n (2 раз n ), и все комнаты с нечетными номерами (которые счётно бесконечны) будут свободны для новых гостей.

Бесконечно много тренеров, у каждого бесконечно много гостей [ править ]

Можно разместить бесконечно много вагонов со счетно бесконечным количеством пассажиров в каждом, используя несколько различных методов. Большинство методов зависят от того, что места в вагонах уже пронумерованы (или используют аксиому счетного выбора ). Как правило, для решения этой проблемы можно использовать любую функцию сопряжения . Для каждого из этих методов рассмотрим номер места пассажира в автобусе, номер его вагона , а затем числа и введенные в два аргумента функции сопряжения . ${\ displaystyle n}$ ${\ displaystyle c}$ ${\ displaystyle n}$ ${\ displaystyle c}$

Метод основных сил [ править ]

Освободите комнаты с нечетными номерами, отправив гостя из комнаты в комнату , затем поместите груз первого тренера в комнаты , груз второго тренера в комнаты ; в качестве номера вагона мы используем номера, в которых - нечетное простое число . Это решение оставляет некоторые комнаты пустыми (что может быть полезно для отеля, а может и нет); в частности, все нечетные числа, не являющиеся степенями простого числа , например 15 или 847, больше не будут заняты. (Итак, строго говоря, это показывает, что количество прибывших меньше или равно количеству созданных вакансий. Легче показать независимыми средствами, что количество прибывших также больше или равно ${\ displaystyle i}$ ${\ Displaystyle 2 ^ {я}}$ ${\ displaystyle 3 ^ {n}}$ ${\ displaystyle 5 ^ {n}}$ ${\ displaystyle c}$ ${\ displaystyle p ^ {n}}$ ${\ displaystyle p}$ ${\ displaystyle c}$ количество вакансий и, следовательно, то, что они равны , чем модифицировать алгоритм до точного соответствия.) (Алгоритм работает одинаково хорошо, если меняются местами, и , какой бы выбор ни был сделан, он должен применяться единообразно повсюду.) ${\ displaystyle n}$ ${\ displaystyle c}$

Метод факторизации простых чисел [ править ]

Вы можете поместить каждого человека, занимающего определенное место, и тренера в комнату (предполагая, что c = 0 для людей, уже находящихся в отеле, 1 для первого тренера и т. Д.). Поскольку каждое число имеет уникальное разложение на простые множители , легко увидеть, что у всех людей будет комната, в то время как никакие два человека не окажутся в одной комнате. Например, человек в комнате 2592 ( ) сидел в 4-м вагоне на 5-м месте. Как и метод простых степеней, это решение оставляет некоторые комнаты пустыми. ${\ displaystyle s}$ ${\ displaystyle c}$ ${\ displaystyle 2 ^ {s} 3 ^ {c}}$ ${\ displaystyle 2 ^ {5} 3 ^ {4}}$

Этот метод также можно легко расширить для бесконечных ночей, бесконечных входов и т. Д. ... ( ) ${\ displaystyle 2 ^ {s} 3 ^ {c} 5 ^ {n} 7 ^ {e}}$

Метод чередования [ править ]

Для каждого пассажира сравните длину и в любой позиционной системе счисления , например, в десятичной . (Считайте, что каждый житель отеля находится в автобусе №0.) Если какое-либо число короче, добавляйте к нему ведущие нули, пока оба значения не будут иметь одинаковое количество цифр. Чередуйте цифры, чтобы получить номер комнаты: его цифры будут [первая цифра номера тренера] - [первая цифра номера места] - [вторая цифра номера тренера] - [вторая цифра номера места] и т. Д. Гость отеля (вагон № 0) из номера 1729 переезжает в номер 01070209 (т.е. номер 1 070 209). Пассажир на месте 1234 в автобусе 789 идет в комнату 01728394 (т. Е. В комнату 1 728 394). ${\ displaystyle n}$ ${\ displaystyle c}$

В отличие от решения Prime Powers, это решение полностью заполняет отель, и мы можем реконструировать оригинальный автобус и кресло гостя, изменив процесс чередования. Сначала добавьте начальный ноль, если в комнате нечетное количество цифр. Затем разделите номер на два числа: номер тренера состоит из нечетных цифр, а номер места - из четных. Конечно, исходная кодировка произвольна, и роли двух чисел можно поменять местами (нечетное место и четное место), если оно применяется последовательно.

Метод треугольных чисел [ править ]

Те, кто уже находится в отеле, будут перемещены в номер или в -й треугольный номер . Те, кто в вагоне, будут в комнате , или треугольное число плюс . Таким образом, все комнаты будут заполнены одним и только одним гостем. ${\ Displaystyle (п ^ {2} + п) / 2}$ ${\ displaystyle n}$ ${\ Displaystyle ((с + п-1) ^ {2} + с + п-1) / 2 + п}$ ${\ Displaystyle (с + п-1)}$ ${\ displaystyle n}$

Эту функцию сопряжения можно продемонстрировать визуально, построив отель в виде пирамиды бесконечно высокой высоты в одну комнату . Самый верхний ряд пирамиды - это отдельная комната: комната 1; его второй ряд - комнаты 2 и 3; и так далее. Столбец, образованный множеством крайних правых комнат, будет соответствовать треугольным числам. После того, как они будут заполнены (перераспределенными жителями отеля), оставшиеся пустые комнаты образуют форму пирамиды, точно идентичную первоначальной форме. Таким образом, процесс может повторяться для каждого бесконечного множества. Выполнение этого по одному для каждого тренера потребует бесконечного количества шагов, но, используя предыдущие формулы, гость может определить, какой будет его комната после того, как его тренер будет достигнут в процессе, и может просто пойти туда. немедленно.

Метод произвольного перебора [ править ]

Пусть . счетно, так как счетно, поэтому мы можем перечислить его элементы . Теперь, если назначить th гостя th тренера в th комнату (считать гостей, уже находящихся в отеле, гостями th тренера). Таким образом, у нас есть функция, назначающая каждого человека комнате; кроме того, это задание не пропускает никакие комнаты. ${\ Displaystyle S: = \ {(a, b) \ mid a, b \ in \ mathbb {N} \}}$ ${\ displaystyle S}$ ${\ Displaystyle \ mathbb {N}}$ ${\ displaystyle s_ {1}, s_ {2}, \ dots}$ ${\ Displaystyle s_ {п} = (а, б)}$ ${\ displaystyle b}$ ${\ displaystyle a}$ ${\ displaystyle n}$ $0$

Дальнейшие слои бесконечности [ править ]

Предположим, что отель находится рядом с океаном, и прибывает бесконечное количество автомобильных паромов , каждый с бесконечным количеством автобусов, каждый с бесконечным количеством пассажиров. Это ситуация с тремя «уровнями» бесконечности , и она может быть решена расширением любого из предыдущих решений.

Метод разложения на простые множители можно применить, добавив новое простое число для каждого дополнительного слоя бесконечности ( с паромом). $2^{s}3^{c}5^{f}$ $f$

Решение для мощности простых чисел может применяться с дальнейшим возведением в степень простых чисел, что приводит к очень большому количеству комнат даже при небольших входных данных. Например, пассажир на втором месте третьего автобуса на втором пароме (адрес 2-3-2) повысит 2-е нечетное простое число (5) до 49, что является результатом того, что третье нечетное простое число (7) будет возведен в степень своего сиденья номер (2). В этом номере комнаты должно быть более тридцати десятичных цифр.

Метод чередования можно использовать с тремя чередующимися «нитями» вместо двух. Пассажир с адресом 2-3-2 перейдет в комнату 232, а пассажир с адресом 4935-198-82217 - в комнату № 008,402,912,391,587 (начальные нули можно удалить).

Предвидя возможность любого количества уровней бесконечного количества гостей, отель может пожелать выделить комнаты таким образом, чтобы ни одному гостю не приходилось переезжать, независимо от того, сколько гостей прибудет позже. Одним из решений является преобразование адреса каждого прибытия в двоичное число, в котором единицы используются в качестве разделителей в начале каждого уровня, в то время как число внутри данного уровня (например, номер тренера гостя) представлено таким количеством нулей. Таким образом, гость с предыдущим адресом 2-5-1-3-1 (пять бесконечных уровней) перейдет в комнату 10010000010100010 (десятичное число 295458).

В качестве дополнительного шага в этом процессе можно удалить один ноль из каждой части номера; в этом примере новая комната гостя - 101000011001 (2585 в десятичной системе). Это гарантирует, что каждая комната может быть заполнена гипотетическим гостем. Если не прибывают бесконечные группы гостей, то будут заняты только комнаты, которые являются степенью двойки.

Бесконечные уровни вложенности [ править ]

Хотя комнату можно найти для любого конечного числа вложенных бесконечностей людей, это не всегда верно для бесконечного числа слоев, даже если на каждом уровне существует конечное число элементов.

Анализ [ править ]

Парадокс Гильберта - это достоверный парадокс : он приводит к противоречащему интуиции результату, который доказуемо верно. Утверждения «есть гость в каждой комнате» и «гости не могут быть размещены» не равнозначны, когда комнат бесконечно много.

Поначалу такое положение вещей может показаться нелогичным. Свойства «бесконечных наборов вещей» сильно отличаются от свойств «конечных наборов вещей». Парадокс Гранд Отеля Гильберта можно понять, используя теорию трансфинитных чисел Кантора . Таким образом, в то время как в обычной (конечной) гостинице с более чем одним номером, количество нечетных номеров явно меньше, чем общее количество номеров. Однако в удачно названном Гранд-отеле Гильберта количество комнат с нечетными номерами не меньше их общего «количества». В математических терминах, то мощность из подмножества , содержащего нечетные номера такой же , как о мощности множествавсех комнат. Действительно, бесконечные множества характеризуются как множества, у которых есть собственные подмножества одинаковой мощности. Для счетных множеств (множеств с той же мощностью, что и натуральные числа ) эта мощность равна . ^[3] ℵ 0 {\displaystyle \aleph _{0}}

Перефразируя, для любого счетно бесконечного множества существует биективная функция, которая отображает счетно бесконечное множество в множество натуральных чисел, даже если счетное бесконечное множество содержит натуральные числа. Например, набор рациональных чисел - тех чисел, которые можно записать как частное от целых чисел - содержит натуральные числа как подмножество, но не больше, чем набор натуральных чисел, поскольку рациональные числа счетны: существует взаимно однозначное соответствие от от натурального к рациональному.

Ссылки в художественной литературе [ править ]

BBC Learning Zone неоднократно показывала одноразовую образовательную документальную драму 1996 года « Отель Гильберт», действие которой происходило в отеле глазами молодой гостьи Фионы Найт, ее имя - игра слов на языке конечного. Программа была разработана, чтобы познакомить зрителей с концепцией бесконечности. ^[4]
Роман Белого свет от математик / научной фантастики писателя Рюкер включает в себя отель , основываясь на парадоксе Гильберта, и где главный герой рассказа встречает Георг Кантор .
В научно-фантастическом романе Стивена Бакстера « Трансцендент» содержится краткое обсуждение природы бесконечности с объяснением, основанным на парадоксе, модифицированном для использования солдат звездолета, а не отелей.
В рассказе Джеффри А. Лэндиса " Туманность " " Рябь в море Дирака " гостиница Гильберта используется как объяснение того, почему бесконечно полное море Дирака все же может принимать частицы.
В романе Питера Хёга «Чувство снега» «Мисс Смилла» главная героиня размышляет о том, что для менеджера и гостей отеля замечательно приложить все усилия, чтобы опоздавший мог иметь свою комнату и немного уединения.
В детском романе Ивара Экланда « Кот в стране чисел » «мистер Гильберт» и его жена управляют бесконечным отелем для всех целых чисел. История развивается по треугольному методу рациональных чисел.
В романе Уилла Уайлса The Way Inn о бесконечно большом мотеле злодея зовут Гильберт.
В романе Реджинальда Хилла «Чужой дом» персонаж Сэм ссылается на парадокс Гилберта в отеле.
Рассказ Наума Я. Виленкин «Необыкновенный отель» (часто ошибочно приписываемый Станиславу Лему ) показывает, как можно переставить гранд-отель Гильберта, когда прибудет бесконечное количество новых хозяев.
Джон Родерик и Кен Дженнингс обсуждали отель в своем подкасте «Омнибус» в эпизоде «Вход в отель Гильберта» .
В саге о комиксах «Буря» из серии « Лига выдающихся джентльменов » Алана Мура и Кевина О'Нила показан злодей по имени Бесконечность. В сюжете предполагается, что злодей отправляется в отель на основании парадокса Гильберта. Упоминается также Георг Кантор .

См. Также [ править ]

Список парадоксов
Парадокс Банаха – Тарского
Парадокс Галилея
Парадоксы теории множеств
Принцип голубятни

Ссылки [ править ]

^ Краг, Хельге (2014). "Правдивая (?) История бесконечного отеля Гильберта". arXiv : 1403.0059 .
^ Гамов, Джордж (1947). Один, два, три ... бесконечность: факты и предположения науки . Нью-Йорк: Viking Press. п. 17.
^ Ракер, Руди (1984) [1982]. Бесконечность и разум. Наука и философия бесконечного . Паладин. С. 73–78. ISBN 0-586-08465-7.
^ https://www.imdb.com/title/tt0443537/

Гильберт, Дэвид (2013), Эвальд, Уильям; Зиг, Вильфрид (ред.), Лекции Дэвида Гильберта по основам арифметики и логики 1917-1933 гг. , Гейдельберг: Springer-Verlag, DOI : 10.1007 / 978-3-540-69444-1 , ISBN 978-3-540-20578-4

Внешние ссылки [ править ]

Бесконечный отель Гильберта . М. Хазевинкель. Энциклопедия математики , Springer. Доступ 25 мая 2007 г.
Нэнси Кейси, добро пожаловать в отель Infinity! - Парадокс, рассказанный как юмористический рассказ о владельце отеля и строительном подрядчике, основан на враждующих математиках XIX века Георге Канторе и Леопольде Кронекере.
Стивен Строгац, The Hilbert Hotel , NY Times, 9 мая 2010 г.
Бесконечный отель Гильберта , h2g2
Отель Гильберт - презентация на YouTube
«За гранью конечного»
см. песню на стр. 704 Американского математического ежемесячника за октябрь 2006 г. или стр. 177 журнала Journal of Mathematics and the Arts за декабрь 2011 г.
Бесконечный парадокс отеля - Джефф Декофски - Уроки TED-Ed

[1] Краг, Хельге (2014). "Правдивая (?) История бесконечного отеля Гильберта". arXiv : 1403.0059 .

[2] Гамов, Джордж (1947). Один, два, три ... бесконечность: факты и предположения науки . Нью-Йорк: Viking Press. п. 17.

[Rucker-3] Ракер, Руди (1984) [1982]. Бесконечность и разум. Наука и философия бесконечного . Паладин. С. 73–78. ISBN 0-586-08465-7.

[4] ttps://www.imdb.com/title/tt0443537/

[1]