Монотонная функция

Рис. 1. Монотонно неубывающая функция.

Рис. 2. Монотонно невозрастающая функция.

Рисунок 3. Функция А , что это не монотонна

В математике , А монотонная функция (или монотонная функция ) является функцией от упорядоченных множеств , что сохраняет или реверсирует данный порядок . ^{[1] [2] [3]} Эта концепция впервые возникла в исчислении , а затем была обобщена на более абстрактные условия теории порядка .

В исчислении и анализе

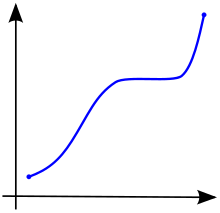
В исчислении , функция , определенная на подмножестве из действительных чисел с реальными значениями называется монотонной , если и только если оно либо полностью не возрастает, либо полностью не убывает. ^[2] То есть, как показано на рис. 1, функция, которая монотонно увеличивается, не обязательно должна увеличиваться исключительно, она просто не должна уменьшаться.${\ displaystyle f}$

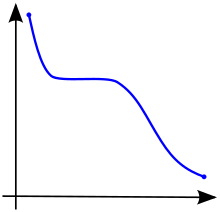
Функция называется монотонно возрастающей (также возрастающей или неубывающей ), ^[3] если для всех и таких, что есть , то сохраняет порядок (см. Рисунок 1). Точно так же функция называется монотонно убывающей (также убывающей или невозрастающей ) ^[3], если, когда-либо , то она меняет порядок (см. Рисунок 2).${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x \ leq y}$${\ Displaystyle е \! \ влево (х \ вправо) \ Leq е \! \ влево (у \ вправо)}$${\ displaystyle f}$${\ displaystyle x \ leq y}$${\displaystyle f\!\left(x\right)\geq f\!\left(y\right)}$

Если порядок в определении монотонности заменить строгим порядком , то получится более сильное требование. Функция с этим свойством называется строго возрастающей (также возрастающей ). ^{[3] [4]} Опять же, инвертируя символ порядка, можно найти соответствующее понятие, называемое строго убывающим (также убывающим ). ^{[3] [4]} Функцию можно назвать строго монотонной, если она либо строго возрастает, либо строго убывает. Функции, которые являются строго монотонными, взаимно однозначны (потому что for not equal to , либо, либо${\displaystyle \leq }$${\displaystyle <}$${\displaystyle x}$${\displaystyle y}$${\displaystyle x<y}$${\displaystyle x>y}$и так, по монотонности, либо или , таким образом .)${\displaystyle f\!\left(x\right)<f\!\left(y\right)}$${\displaystyle f\!\left(x\right)>f\!\left(y\right)}$${\displaystyle f\!\left(x\right)\neq f\!\left(y\right)}$

Если неясно, что «увеличение» и «уменьшение» включают возможность повторения одного и того же значения при последовательных аргументах, можно использовать термины « слабо монотонный» , « слабо увеличивающийся» и « слабо убывающий», чтобы подчеркнуть эту возможность.

Термины «не убывающий» и «не возрастающий» не следует путать с (гораздо более слабыми) отрицательными квалификациями «не убывающий» и «не возрастающий». Например, функция на фиг.3 сначала падает, затем возрастает, а затем снова падает. Следовательно, он не убывает и не увеличивается, но и не не убывает, и не увеличивает.

Функция называется абсолютно монотонна на интервале , если производные всех порядков являются неотрицательно или все неположительны во всех точках интервала.${\displaystyle f\!\left(x\right)}$${\displaystyle \left(a,b\right)}$${\displaystyle f}$

Обратная функция

Функция, которая является монотонной, но не строго монотонной и, следовательно, постоянной на интервале, не имеет обратного. Это связано с тем, что для того, чтобы функция имела инверсию, необходимо взаимно однозначное отображение диапазона в домен функции. Поскольку у монотонной функции есть некоторые значения, которые являются постоянными в ее области, это означает, что в диапазоне, который отображается на это постоянное значение, может быть более одного значения.

Однако функция y = g ( x ), которая является строго монотонной, имеет обратную функцию, такую ​​что x = h ( y ), потому что всегда гарантируется взаимно-однозначное отображение диапазона в область определения функции. Кроме того, можно сказать, что функция строго монотонна для диапазона значений и, следовательно, имеет инверсию для этого диапазона значений. Например, если y = g ( x ) строго монотонен в диапазоне [ a , b ] , то он имеет обратный x = h ( y) на диапазоне [ g ( a ), g ( b )] , но мы не можем сказать, что весь диапазон функции имеет обратный.

Обратите внимание, какие учебники ^{[ какие? ]} ошибочно заявляют, что обратное существует для монотонной функции, когда на самом деле они означают, что обратное существует для строго монотонной функции.

Монотонное преобразование

Термин монотонное преобразование (или монотонное преобразование ) также может вызвать некоторую путаницу, поскольку он относится к преобразованию с помощью строго возрастающей функции. Так обстоит дело в экономике в отношении порядковых свойств функции полезности , сохраняемых при монотонном преобразовании (см. Также монотонные предпочтения ). ^[5] В этом контексте то, что мы называем «монотонным преобразованием», точнее, называется «положительным монотонным преобразованием», чтобы отличить его от «отрицательного монотонного преобразования», которое меняет порядок чисел на обратный. ^[6]

Некоторые основные приложения и результаты

Для монотонной функции верны следующие свойства :${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$

• ${\displaystyle f}$имеет пределы справа и слева в каждой точке своей области ;
• ${\displaystyle f}$имеет предел в положительной или отрицательной бесконечности ( ) действительного числа , или .${\displaystyle \pm \infty }$${\displaystyle \infty }$${\displaystyle -\infty }$
• ${\displaystyle f}$может иметь только скачкообразные разрывы ;
• ${\displaystyle f}$может иметь только счетное количество разрывов в своей области. Однако разрывы не обязательно состоят из изолированных точек и даже могут быть плотными в интервале ( a , b ). ^{[ необходим пример ]}

Эти свойства являются причиной того, почему монотонные функции полезны в технической работе по анализу . Еще несколько фактов об этих функциях:

• если есть монотонная функция , определенная на отрезке , то есть дифференцируема почти всюду на ; то есть набор чисел в таких , что не является дифференцируемой в имеет лебегову меру нуль . Кроме того, этот результат нельзя улучшить до счетного: см. Функцию Кантора .${\displaystyle f}$ ${\displaystyle I}$${\displaystyle f}$ ${\displaystyle I}$${\displaystyle x}$${\displaystyle I}$${\displaystyle f}$${\displaystyle x}$
• если это множество счетно, то оно абсолютно непрерывно.${\displaystyle f}$
• если есть монотонная функция , определенная на отрезке , то есть Риман .${\displaystyle f}$${\displaystyle \left[a,b\right]}$${\displaystyle f}$

Важное применение монотонных функций - теория вероятностей . Если - случайная величина , ее кумулятивная функция распределения является монотонно возрастающей функцией.${\displaystyle X}$ ${\displaystyle F_{X}\!\left(x\right)={\text{Prob}}\!\left(X\leq x\right)}$

Функция является унимодальной, если она монотонно возрастает до некоторой точки ( мода ), а затем монотонно убывает.

Когда это строго монотонная функция, то есть инъективны на своей области, и если это диапазон от , то есть обратная функция на для . Напротив, каждая постоянная функция является монотонной, но не инъективной ^[7] и, следовательно, не может иметь обратной.${\displaystyle f}$${\displaystyle f}$${\displaystyle T}$${\displaystyle f}$${\displaystyle T}$${\displaystyle f}$

В топологии

Карта называется монотонной, если каждый ее слой связен; т.е. для каждого элемента в (возможно, пустом) наборе связан.${\displaystyle f:X\rightarrow Y}$${\displaystyle y}$${\displaystyle Y}$${\displaystyle f^{-1}(y)}$

В функциональном анализе

В функциональном анализе на топологическом векторном пространстве , (возможно , нелинейный) оператор называется быть монотонным оператором , если${\displaystyle X}$${\displaystyle T:X\rightarrow X^{*}}$

${\displaystyle (Tu-Tv,u-v)\geq 0\quad \forall u,v\in X.}$

Теорема Качуровского показывает, что выпуклые функции на банаховых пространствах имеют монотонные операторы в качестве производных.

Подмножество из , как говорят, является монотонное множество , если для каждой пары , и в ,${\displaystyle G}$${\displaystyle X\times X^{*}}$${\displaystyle [u_{1},w_{1}]}$${\displaystyle [u_{2},w_{2}]}$${\displaystyle G}$

${\displaystyle (w_{1}-w_{2},u_{1}-u_{2})\geq 0.}$

${\displaystyle G}$называется максимальной монотонностью, если она максимальна среди всех монотонных множеств в смысле включения множеств. График монотонного оператора - это монотонное множество. Монотонный оператор называется максимальным монотонным, если его график является максимальным монотонным множеством .${\displaystyle G(T)}$

В порядке теории

Теория порядка имеет дело с произвольными частично упорядоченными наборами и предварительно упорядоченными наборами как обобщением действительных чисел. Приведенное выше определение монотонности актуально и в этих случаях. Однако термины «увеличение» и «уменьшение» избегаются, поскольку их обычное графическое представление не применяется к заказам, которые не являются общими . Кроме того, строгие отношения <и> мало используются во многих неполных порядках, и поэтому для них не вводится дополнительная терминология.

Обозначение ≤ обозначает отношение частичного порядка любого частично упорядоченного множества, монотонную функцию, также называемую изотонной , илисохраняющий порядок , удовлетворяет свойству

x ≤ y влечет f ( x ) ≤ f ( y ),

для всех x и y в своей области. Композиция двух монотонных отображений также монотонна.

Двойное понятие часто называют антитонен , анти-монотонной , или порядок реверсирования . Следовательно, антитонная функция f удовлетворяет свойству

x ≤ y влечет f ( y ) ≤ f ( x ),

для всех x и y в своей области.

Функция постоянной одновременно монотонно и антитонен; наоборот, если f является одновременно монотонным и антитонным, и если область определения f является решеткой , то f должно быть постоянным.

Монотонные функции занимают центральное место в теории порядка. Они появляются в большинстве статей по данной теме, и в этих местах можно найти примеры из специальных приложений. Некоторые известные специальные монотонные функции - это порядковые вложения (функции, для которых x ≤ y, если и только если f ( x ) ≤ f ( y )) и порядковые изоморфизмы ( сюръективные порядковые вложения).

В контексте поисковых алгоритмов

В контексте алгоритмов поиска монотонность (также называемая согласованностью) - это условие, применяемое к эвристическим функциям . Эвристика h (n) является монотонной, если для каждого узла n и каждого последователя n ' из n, порожденного любым действием a , оценочная стоимость достижения цели из n не превышает стоимость шага перехода к n' плюс ориентировочная стоимость достижения цели от n ' ,

${\displaystyle h(n)\leq c\left(n,a,n'\right)+h\left(n'\right).}$

Это форма неравенства треугольника с n , n ' и целью G _n, ближайшей к n . Поскольку любая монотонная эвристика также допустима , монотонность является более строгим требованием, чем допустимость. Некоторые эвристические алгоритмы, такие как A *, могут быть признаны оптимальными при условии, что эвристика, которую они используют, является монотонной. ^[8]

В булевых функциях

В булевой алгебре монотонная функция - это такая функция, что для всех a _i и b _i в {0,1}, если a ₁ ≤ b ₁ , a ₂ ≤ b ₂ , ..., a _n ≤ b _n (т. Е. Декартово произведение {0, 1} ⁿ упорядочено покоординатно ), тогда f ( a ₁ , ..., a _n ) ≤ f ( b ₁ , ..., b _n ). Другими словами, логическая функция является монотонной, если для каждой комбинации входов переключение одного из входов с ложного на истинное может только вызвать переключение вывода с ложного на истинное, а не с истинного на ложное. Графически это означает, что n- мерная логическая функция является монотонной, когда ее представление в виде n -куба, помеченного значениями истинности, не имеет восходящего ребра от истины до ложи . (Этот меченный диаграмма , Хасса является двойным меченой функцией в диаграмме Венны , которая является более общим представлением для п ≤ 3 ) .

Монотонные логические функции - это как раз те, которые могут быть определены выражением, объединяющим входные данные (которые могут появляться более одного раза) с использованием только операторов и и или (в частности, не запрещено). Например, «по крайней мере два из a , b , c имеют место» является монотонной функцией от a , b , c , так как это может быть записано, например, как (( a и b ) или ( a и c ) или ( b и c) )).

Количество таких функций от n переменных известно как число Дедекинда для n .

Смотрите также

• Монотонная кубическая интерполяция
• Псевдомонотонный оператор
• Коэффициент ранговой корреляции Спирмена - мера монотонности в наборе данных
• Полная монотонность
• Циклическая монотонность
• Операторная монотонная функция

Примечания

Библиография

• Бартл, Роберт Г. (1976). Элементы реального анализа (2-е изд.).
• Гретцер, Джордж (1971). Теория решеток: первые понятия и распределительные решетки . ISBN 0-7167-0442-0.
• Пембертон, Малькольм; Рау, Николай (2001). Математика для экономистов: вводный учебник . Издательство Манчестерского университета. ISBN 0-7190-3341-1.
• Ренарди, Майкл и Роджерс, Роберт С. (2004). Введение в уравнения в частных производных . Тексты по прикладной математике 13 (второе изд.). Нью-Йорк: Springer-Verlag. п. 356. ISBN. 0-387-00444-0.
• Рис, Фриджес и Бела Сёкефалви-Надь (1990). Функциональный анализ . Courier Dover Publications. ISBN 978-0-486-66289-3.
• Рассел, Стюарт Дж .; Норвиг, Питер (2010). Искусственный интеллект: современный подход (3-е изд.). Река Аппер Сэдл, Нью-Джерси: Prentice Hall. ISBN 978-0-13-604259-4.
• Саймон, Карл П .; Блюм, Лоуренс (апрель 1994). Математика для экономистов (первое изд.). ISBN 978-0-393-95733-4. (Определение 9.31)

внешняя ссылка

• «Монотонная функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Конвергенция монотонной последовательности Аник Дебнат и Томас Роксло (Школа Харкера), Демонстрационный проект Вольфрама .
• Вайсштейн, Эрик В. «Монотонная функция» . MathWorld .