В математике , прокладка аполлоническая или аполлоническая сетка является фрактальной генерируется исходя из тройки окружностей, каждая касательная к двум другим, и последовательно заполняя более кругов, каждый касательную к другим трем. Он назван в честь греческого математика Аполлония Пергского . [1]
Строительство [ править ]
Аполлоновскую прокладку можно построить следующим образом. Начните с трех окружностей C 1 , C 2 и C 3 , каждая из которых касается двух других (в общей конструкции эти три окружности должны быть разных размеров и иметь общую касательную). Аполлоний обнаружил, что есть две другие непересекающиеся окружности, C 4 и C 5 , которые обладают тем свойством, что они касаются всех трех исходных окружностей - они называются аполлоновскими окружностями . Добавив два аполлонических круга к исходным трем, мы получим пять кругов.
Возьмите один из двух аполлонических кругов - скажем C 4 . Он касается C 1 и C 2 , поэтому тройка окружностей C 4 , C 1 и C 2 имеет свои две аполлоновские окружности. Мы уже знаем один из них - это C 3, но другой - новый круг C 6 .
Аналогичным образом мы можем построить еще одну новую окружность C 7 , касательную к C 4 , C 2 и C 3 , и еще одну окружность C 8 из C 4 , C 3 и C 1 . Это дает нам 3 новых круга. Мы можем построить еще три новых круга из C 5 , получив в целом шесть новых кругов. Вместе с кругами от C 1 до C 5 это дает в общей сложности 11 кругов.
Продолжая поэтапно строительство таким образом, мы можем добавить 2 · 3 n новых кругов на этапе n , что в сумме даст 3 n +1 + 2 круга после n этапов. В пределе этот набор кругов является прокладкой Аполлона.
Размеры новых кругов определяются теоремой Декарта . Обозначим через k i (для i = 1, ..., 4) кривизны четырех касательных друг к другу окружностей. Тогда теорема Декарта утверждает
( 1 )
Аполлоновская прокладка имеет размер Хаусдорфа около 1,3057. [2]
Кривизна [ править ]
Кривизна окружности (изгиба) определяется как обратная ее радиусу.
- Отрицательная кривизна указывает на то, что все остальные круги касаются этой окружности изнутри. Это ограничивающий круг.
- Нулевая кривизна дает линию (круг с бесконечным радиусом).
- Положительная кривизна указывает на то, что все остальные круги касаются этой окружности снаружи. Этот круг находится внутри круга с отрицательной кривизной.
Варианты [ править ]
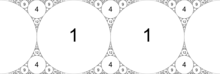
Прокладку Аполлона также можно построить, заменив одну из образующих окружностей прямой линией, которую можно рассматривать как окружность, проходящую через бесконечно удаленную точку.
В качестве альтернативы, две образующие окружности можно заменить параллельными прямыми линиями, которые можно рассматривать как касательные друг к другу на бесконечности. В этой конструкции дополнительные круги образуют семейство кругов Форда .
Трехмерный эквивалент аполлонической прокладки - сферическая аполлоническая упаковка .
Симметрии [ править ]
Если две из исходных образующих окружностей имеют одинаковый радиус, а третья окружность имеет радиус, составляющий две трети от этого, то прокладка Аполлона имеет две линии отражательной симметрии; одна линия - линия, соединяющая центры одинаковых окружностей; другая - их касательная, проходящая через центр третьего круга. Эти линии перпендикулярны друг другу, поэтому аполлоническая прокладка также имеет вращательную симметрию степени 2; группа симметрии этой прокладки - D 2 .
Если все три исходных образующих окружности имеют одинаковый радиус, тогда прокладка Аполлона имеет три линии отражающей симметрии; эти прямые являются взаимными касательными каждой пары окружностей. Каждая взаимная касательная также проходит через центр третьего круга и общий центр первых двух аполлонических кругов. Эти линии симметрии расположены под углами в 60 градусов друг к другу, поэтому аполлоническая прокладка также имеет вращательную симметрию степени 3; группа симметрии этой прокладки - D 3 .
Ссылки с гиперболической геометрией [ править ]
Три образующих круга, а значит, и вся конструкция, определяются положением трех точек, в которых они касаются друг друга. Поскольку существует преобразование Мёбиуса, которое отображает любые три заданные точки на плоскости в любые другие три точки, и поскольку преобразования Мёбиуса сохраняют окружности, то существует преобразование Мёбиуса, которое переводит любые две аполлоновские прокладки друг в друга.
Преобразования Мёбиуса также являются изометриями гиперболической плоскости , поэтому в гиперболической геометрии все аполлоновские прокладки конгруэнтны. Таким образом, в некотором смысле существует только одна аполлоновская прокладка с точностью до (гиперболической) изометрии.
Прокладка Аполлона - это предельное множество группы преобразований Мёбиуса, известной как группа Кляйниана . [3]
Интегральные аполлонические окружности [ править ]
Интегральная аполлоническая упаковка кругов, определяемая кривизной окружности (−1, 2, 2, 3)
Интегральная аполлоническая упаковка кругов, определяемая кривизной окружности (−3, 5, 8, 8)
Интегральная аполлоническая упаковка кругов, определяемая кривизной окружности (−12, 25, 25, 28)
Интегральная аполлоническая упаковка кругов, определяемая кривизной окружности (−6, 10, 15, 19)
Интегральная аполлоническая упаковка кругов, определяемая кривизной окружности (−10, 18, 23, 27)
Если любые четыре касательных друг к другу окружности в аполлонической прокладке имеют целочисленную кривизну, то все круги в прокладке будут иметь целочисленную кривизну. [4] Поскольку уравнение, связывающее кривизну в аполлоновской прокладке, целое или нет, имеет вид
из этого следует, что с помощью прыжка Виета можно перейти от одной четверки кривизны к другой , как при нахождении нового числа Маркова . Первые несколько из этих встроенных аполлонических прокладок перечислены в следующей таблице. В таблице указаны кривизны самых больших окружностей прокладки. Только первые три кривизны (из пяти, показанных в таблице) необходимы для полного описания каждой прокладки - все остальные кривизны могут быть получены из этих трех.
|
Симметрия интегральных аполлонических окружностей [ править ]
Нет симметрии [ править ]
Если ни одна из кривизны не повторяется в пределах первых пяти, прокладка не содержит симметрии, которая представлена группой симметрии C 1 ; прокладка, описываемая кривизной (-10, 18, 23, 27), является примером.
D 1 симметрия [ править ]
Когда два из пяти наибольших кругов в прокладке имеют одинаковую кривизну, эта прокладка будет иметь симметрию D 1 , что соответствует отражению вдоль диаметра ограничивающей окружности без симметрии вращения.
Симметрия D 2 [ править ]
Если две разные кривизны повторяются в пределах первых пяти, прокладка будет иметь симметрию D 2 ; такая симметрия состоит из двух отражений (перпендикулярных друг другу) вдоль диаметров ограничивающей окружности с двойной симметрией поворота 180 °. Прокладка, описываемая кривизной (-1, 2, 2, 3), является единственной аполлонической прокладкой (с точностью до масштабного коэффициента), обладающей симметрией D 2 .
Симметрия D 3 [ править ]
Целочисленных прокладок с симметрией D 3 не существует .
Если три круга с наименьшей положительной кривизной имеют одинаковую кривизну, прокладка будет иметь симметрию D 3 , что соответствует трем отражениям по диаметрам ограничивающей окружности (разнесенной на 120 °), а также тройной симметрии вращения 120 °. В этом случае отношение кривизны ограничивающей окружности к трем внутренним окружностям составляет 2 √ 3 - 3. Поскольку это соотношение нерационально, никакие интегральные аполлоновские упаковки окружностей не обладают этой симметрией D 3 , хотя многие упаковки подходят близко.
Почти симметрия D 3 [ править ]
Фигура слева представляет собой интегральную аполлоновскую прокладку, имеющую симметрию D 3 . Тот же рисунок показан справа, с метками, указывающими кривизну внутренних окружностей, демонстрируя, что прокладка фактически обладает только симметрией D 1, общей для многих других интегральных аполлоновских прокладок.
В следующей таблице перечислены несколько из этих почти - D 3 интегральных прокладок Аполлона. Последовательность имеет несколько интересных свойств, и в таблице перечислены факторизация кривизны вместе с множителем, необходимым для перехода от предыдущего набора к текущему. Абсолютные значения кривизны дисков "a" подчиняются рекуррентному соотношению a ( n ) = 4 a ( n - 1) - a ( n - 2) (последовательность A001353 в OEIS ), из которого следует, что множитель сходится к √ 3 + 2 ≈ 3,732050807.
| Кривизна | Факторы | Множитель | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| а | б | c | d | а | б | d | а | б | c | d | ||
| −1 | 2 | 2 | 3 | 1 × 1 | 1 × 2 | 1 × 3 | Нет данных | Нет данных | Нет данных | Нет данных | ||
| −4 | 8 | 9 | 9 | 2 × 2 | 2 × 4 | 3 × 3 | 4,000000000 | 4,000000000 | 4,500000000 | 3.000000000 | ||
| −15 | 32 | 32 | 33 | 3 × 5 | 4 × 8 | 3 × 11 | 3,750000000 | 4,000000000 | 3,555555556 | 3,666666667 | ||
| −56 | 120 | 121 | 121 | 8 × 7 | 8 × 15 | 11 × 11 | 3,733333333 | 3,750000000 | 3,781250000 | 3,666666667 | ||
| −209 | 450 | 450 | 451 | 11 × 19 | 15 × 30 | 11 × 41 | 3,732142857 | 3,750000000 | 3,719008264 | 3,727272727 | ||
| −780 | 1680 | 1681 | 1681 | 30 × 26 | 30 × 56 | 41 × 41 | 3,732057416 | 3,733333333 | 3,735555556 | 3,727272727 | ||
| −2911 | 6272 | 6272 | 6273 | 41 × 71 | 56 × 112 | 41 × 153 | 3,732051282 | 3,733333333 | 3,731112433 | 3,731707317 | ||
| −10864 | 23408 | 23409 | 23409 | 112 × 97 | 112 × 209 | 153 × 153 | 3,732050842 | 3,732142857 | 3,732302296 | 3,731707317 | ||
| −40545 | 87362 | 87362 | 87363 | 153 × 265 | 209 × 418 | 153 × 571 | 3,732050810 | 3,732142857 | 3,731983425 | 3,732026144 | ||
Последовательные искривления [ править ]
Для любого целого n > 0 существует аполлоновская прокладка, определяемая следующими кривизнами:
(- n , n + 1, n ( n + 1), n ( n + 1) + 1).
Например, прокладки, обозначенные (−2, 3, 6, 7), (−3, 4, 12, 13), (−8, 9, 72, 73) и (−9, 10, 90, 91 ) все следуют этому шаблону. Поскольку каждая внутренняя окружность, определяемая параметром n + 1, может стать ограничивающей окружностью (определяемой параметром - n ) в другой прокладке, эти прокладки могут быть вложенными . Это показано на рисунке справа, который содержит эти последовательные прокладки с n от 2 до 20.
См. Также [ править ]
- Теорема Декарта , для кривизны взаимно касательных окружностей
- Круг Форда , частный случай цельной аполлонической прокладки (0,0,1,1)
- Серпинский треугольник
- Аполлоновская сеть , граф, полученный из конечных подмножеств аполлоновской прокладки
Примечания [ править ]
- ^ Сатия, II, Бабочка в мире Иглесиаса Васиаса: История самого увлекательного квантового фрактала ( Бристоль : IOP Publishing , 2016), стр. 5 .
- ↑ McMullen, Curtis T. (3 октября 1997 г.). « Хаусдорфова размерность и конформная динамика III: вычисление размерности », Abel.Math.Harvard.edu . Доступ: 27 октября 2018 г.
- ^ Счетные круги и эргодическая теория клейнианских групп Хи О Брауна. Университет декабрь 2009 г.
- ^ Рональд Л. Грэм, Джеффри С. Lagarias, Колин М. Маллоус, Алан Р. Уилкс, и Кэтрин Х. Ян; "Аполлонические упаковки кругов: теория чисел" J. Теория чисел, 100 (2003), 1-45
Ссылки [ править ]
- Бенуа Б. Мандельброт: фрактальная геометрия природы , WH Freeman, 1982, ISBN 0-7167-1186-9
- Пол Д. Бурк: « Введение во фрактал Аполлонии ». Компьютеры и графика, том 30, выпуск 1, январь 2006 г., страницы 134–136.
- Дэвид Мамфорд , Серия Кэролайн , Дэвид Райт: Жемчужины Индры: видение Феликса Кляйна , Cambridge University Press, 2002, ISBN 0-521-35253-3
- Джеффри К. Лагариас, Колин Л. Мэллоуз, Аллан Р. Уилкс: за пределами теоремы Декарта о круге , The American Mathematical Monthly, Vol. 109, No. 4 (апрель 2002 г.), стр. 338–361, ( arXiv: math.MG/0101066 v1 9 января 2001 г. )
Внешние ссылки [ править ]
| В Wikibook Fractals есть страница по теме: Аполлонические фракталы |
- Вайсштейн, Эрик В. «Аполлоновская прокладка» . MathWorld .
- Александр Богомольный , Apollonian Gasket , разрубить узел
- Интерактивная аполлоническая прокладка, работающая на чистом HTML5 (ссылка мертва)
- (на английском языке) Сценарий Matlab для построения 2D аполлонической прокладки с n идентичными кругами с использованием инверсии кругов
- Онлайн-эксперименты с JSXGraph
- Аполлоническая прокладка Майкла Скрайбера, Демонстрационный проект Вольфрама .
- Интерактивная демонстрация аполлонической прокладки, работающая на Java
- Дана Маккензи. Тискет, шкатулка, аполлонийская прокладка . Американский ученый, январь / февраль 2010 г.
- «Песок, рисующий крупнейшее в мире произведение искусства» , The Telegraph , 16 декабря 2009 г.. Газетный рассказ о произведении искусства в виде частичной аполлонической прокладки с внешней окружностью в девять миль.
- (на итальянском языке) Динамические аполлонические прокладки , Тартапелаго Джорджо Пьетрокола, 2014 г.




