Интервальный конечный элемент

Эта статья включает в себя список общих ссылок , но он остается в значительной степени непроверенным, поскольку в нем отсутствует достаточное количество соответствующих встроенных ссылок . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Январь 2010 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

Максимальное напряжение по Мизесу в задаче о плоских напряжениях с интервальными параметрами (рассчитывается градиентным методом).

В численном анализе , то интервал метод конечных элементов ( интервал ПЭМ ) представляет собой метод конечных элементов , который использует параметры интервала. Интервальный МКЭ может применяться в ситуациях, когда невозможно получить достоверные вероятностные характеристики конструкции. Это важно в бетонных конструкциях, деревянных конструкциях, геомеханике, композитных конструкциях, биомеханике и во многих других областях. ^[1] Цель интервала конечного элемента - найти верхнюю и нижнюю границы различных характеристик модели (например, напряжение , перемещения , поверхность текучестии т. д.) и использовать эти результаты в процессе проектирования. Это так называемый проект наихудшего случая, который тесно связан с расчетом по предельному состоянию .

Планирование наихудшего случая требует меньше информации, чем вероятностный план, однако результаты более консервативны [Köylüoglu and Elishakoff 1998]. ^{[ необходима цитата ]}

Применение интервальных параметров к моделированию неопределенности [ править ]

Рассмотрим следующее уравнение:

${\ displaystyle ax = b \,}$

где a и b - действительные числа , и .${\ displaystyle x = {\ frac {b} {a}}}$

Очень часто точные значения параметров a и b неизвестны.

Предположим, что и . В этом случае необходимо решить следующее уравнение${\ Displaystyle а \ в [1,2] = \ mathbf {а}}$${\ displaystyle b \ in [1,4] = \ mathbf {b}}$

${\ Displaystyle [1,2] х = [1,4]}$

Существует несколько определений множества решений этого уравнения с интервальными параметрами.

Единый набор решений [ править ]

В этом подходе решением является следующий набор

${\displaystyle \mathbf {x} =\left\{x:ax=b,a\in \mathbf {a} ,b\in \mathbf {b} \right\}={\frac {\mathbf {b} }{\mathbf {a} }}={\frac {[1,4]}{[1,2]}}=[0.5,4]}$

Это наиболее популярный набор решений интервального уравнения, и этот набор решений будет применен в этой статье.

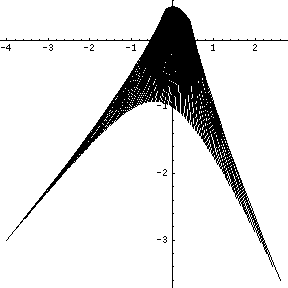
В многомерном случае множество единых решений намного сложнее. Множество решений следующей системы линейных интервальных уравнений

${\displaystyle \left[{\begin{array}{cc}{[-4,-3]}&{[-2,2]}\\{[-2,2]}&{[-4,-3]}\end{array}}\right]\left[{\begin{array}{c}x_{1}\\x_{2}\end{array}}\right]=\left[{\begin{array}{c}{[-8,8]}\\{[-8,8]}\end{array}}\right]}$

показано на следующем рисунке

${\displaystyle \sum {_{\exists \exists }}(\mathbf {A} ,\mathbf {b} )=\{x:Ax=b,A\in \mathbf {A} ,b\in \mathbf {b} \}}$

Набор точных решений очень сложен, поэтому необходимо найти наименьший интервал, который содержит набор точных решений.

${\displaystyle \diamondsuit \left(\sum {_{\exists \exists }}(\mathbf {A} ,\mathbf {b} )\right)=\diamondsuit \{x:Ax=b,A\in \mathbf {A} ,b\in \mathbf {b} \}}$

или просто

${\displaystyle \diamondsuit \left(\sum {_{\exists \exists }}(\mathbf {A} ,\mathbf {b} )\right)=[{\underline {x}}_{1},{\overline {x}}_{1}]\times [{\underline {x}}_{2},{\overline {x}}_{2}]\times ...\times [{\underline {x}}_{n},{\overline {x}}_{n}]}$

куда

${\displaystyle {\underline {x}}_{i}=\min\{x_{i}:Ax=b,A\in \mathbf {A} ,b\in \mathbf {b} \},\ \ {\overline {x}}_{i}=\max\{x_{i}:Ax=b,A\in \mathbf {A} ,b\in \mathbf {b} \}}$

${\displaystyle x_{i}\in \{x_{i}:Ax=b,A\in \mathbf {A} ,b\in \mathbf {b} \}=[{\underline {x}}_{i},{\overline {x}}_{i}]}$

См. Также [1]

Набор параметрических решений интервальной линейной системы [ править ]

Метод интервальных конечных элементов требует решения системы уравнений, зависящих от параметров (обычно с симметричной положительно определенной матрицей). Пример набора решений общей системы уравнений, зависящих от параметров.

${\displaystyle \left[{\begin{array}{cc}p_{1}&p_{2}\\p_{2}+1&p_{1}\end{array}}\right]\left[{\begin{array}{cc}u_{1}\\u_{2}\end{array}}\right]=\left[{\begin{array}{c}{\frac {p_{1}+6p_{2}}{5.0}}\\2p_{1}-6\end{array}}\right],\ \ \ for\ \ p_{1}\in [2,4],p_{2}\in [-2,1].}$

показан на картинке ниже. ^[2]

Алгебраическое решение [ править ]

В этом подходе x - номер интервала, для которого уравнение

${\displaystyle [1,2]x=[1,4]}$

доволен. Другими словами, левая часть уравнения равна правой части уравнения. В этом конкретном случае решение состоит в том, что${\displaystyle x=[1,2]}$

${\displaystyle ax=[1,2][1,2]=[1,4]}$

Если неопределенность больше, т. Е. Потому, что${\displaystyle a=[1,4]}$${\displaystyle x=[1,1]}$

${\displaystyle ax=[1,4][1,1]=[1,4]}$

Если неопределенность еще больше, т. Е. Решения не существует. Найти физическую интерпретацию алгебраического интервального множества решений очень сложно. Таким образом, в приложениях обычно применяется единый набор решений.${\displaystyle a=[1,8]}$

Метод [ править ]

Рассмотрим PDE с интервальными параметрами

${\displaystyle (1)\ \ \ G(x,u,p)=0}$

где - вектор параметров, принадлежащих заданным интервалам${\displaystyle p=(p_{1},\dots ,p_{m})\in {\mathbf {p} }}$

${\displaystyle p_{i}\in [{\underline {p}}_{i},{\overline {p}}_{i}]={\mathbf {p} }_{i},}$

${\displaystyle {\mathbf {p} }={\mathbf {p} }_{1}\times {\mathbf {p} }_{2}\times \cdots \times {\mathbf {p} }_{m}.}$

Например, уравнение теплопередачи

${\displaystyle k_{x}{\frac {\partial ^{2}u}{\partial x^{2}}}+k_{y}{\frac {\partial ^{2}u}{\partial y^{2}}}+q=0{\text{ for }}x\in \Omega }$

${\displaystyle u(x)=u^{*}(x){\text{ for }}x\in \partial \Omega }$

где - параметры интервала (т.е. ).${\displaystyle k_{x},k_{y}}$${\displaystyle k_{x}\in {\mathbf {k} }_{x},\ k_{y}\in {\mathbf {k} }_{y}}$

Решение уравнения (1) можно определить следующим образом

${\displaystyle {\tilde {u}}(x):=\{u(x):G(x,u,p)=0,p\in {\mathbf {p} }\}}$

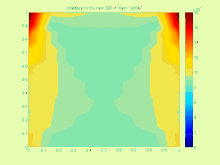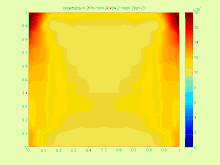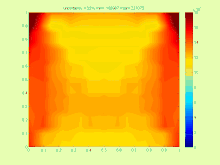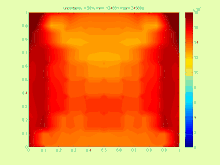
Например, в случае уравнения теплопередачи

${\displaystyle {\tilde {u}}(x)=\{u(x):k_{x}{\frac {\partial ^{2}u}{\partial x^{2}}}+k_{y}{\frac {\partial ^{2}u}{\partial y^{2}}}+q=0{\text{ for }}x\in \Omega ,u(x)=u^{*}(x){\text{ for }}x\in \partial \Omega ,k_{x}\in {\mathbf {k} }_{x},\ k_{y}\in {\mathbf {k} }_{y}\}}$

Решение очень сложное, потому что на практике более интересно найти наименьший возможный интервал, содержащий точное множество решений .${\displaystyle {\tilde {u}}}$${\displaystyle {\tilde {u}}}$

${\displaystyle {\mathbf {u} }(x)=\lozenge {\tilde {u}}(x)=\lozenge \{u(x):G(x,u,p)=0,p\in {\mathbf {p} }\}}$

Например, в случае уравнения теплопередачи

${\displaystyle {\mathbf {u} }(x)=\lozenge \{u(x):k_{x}{\frac {\partial ^{2}u}{\partial x^{2}}}+k_{y}{\frac {\partial ^{2}u}{\partial y^{2}}}+q=0{\text{ for }}x\in \Omega ,u(x)=u^{*}(x){\text{ for }}x\in \partial \Omega ,k_{x}\in {\mathbf {k} }_{x},\ k_{y}\in {\mathbf {k} }_{y}\}}$

Метод конечных элементов приводит к следующей системе алгебраических уравнений, зависящей от параметров

${\displaystyle K(p)u=Q(p),\ \ \ p\in {\mathbf {p} }}$

где K - матрица жесткости, а Q - правая часть.

Интервальное решение можно определить как многозначную функцию

${\displaystyle {\mathbf {u} }=\lozenge \{u:K(p)u=Q(p),p\in {\mathbf {p} }\}}$

В простейшем случае описанную выше систему можно рассматривать как систему линейных интервальных уравнений .

Также возможно определить интервальное решение как решение следующей задачи оптимизации

${\displaystyle {\underline {u}}_{i}=\min\{u_{i}:K(p)u=Q(p),p\in {\mathbf {p} }\}}$

${\displaystyle {\overline {u}}_{i}=\max\{u_{i}:K(p)u=Q(p),p\in {\mathbf {p} }\}}$

В многомерном случае интервальное решение можно записать как

${\displaystyle \mathbf {u} =\mathbf {u} _{1}\times \cdots \times \mathbf {u} _{n}=[{\underline {u}}_{1},{\overline {u}}_{1}]\times \cdots \times [{\underline {u}}_{n},{\overline {u}}_{n}]}$

Интервальное решение против вероятностного решения [ править ]

Важно знать, что параметры интервала дают разные результаты, чем равномерно распределенные случайные величины .

Параметр Interval учитывает все возможные распределения вероятностей (для ).${\displaystyle \mathbf {p} =[{\underline {p}},{\overline {p}}]}$${\displaystyle p\in [{\underline {p}},{\overline {p}}]}$

Для определения параметра интервала необходимо знать только верхнюю и нижнюю границы .${\displaystyle {\overline {p}}}$${\displaystyle {\underline {p}}}$

Расчет вероятностных характеристик требует знания большого количества экспериментальных результатов.

Можно показать, что сумма n интервальных чисел в раз больше, чем сумма подходящих нормально распределенных случайных величин.${\displaystyle {\sqrt {n}}}$

Сумма числа n интервалов равна${\displaystyle \mathbf {p} =[{\underline {p}},{\overline {p}}]}$

${\displaystyle n\mathbf {p} =[n{\underline {p}},n{\overline {p}}]}$

Ширина этого интервала равна

${\displaystyle n{\overline {p}}-n{\underline {p}}=n({\overline {p}}-{\underline {p}})=n\Delta p}$

Рассмотрим нормально распределенную случайную величину X такую, что

${\displaystyle m_{X}=E[X]={\frac {{\overline {p}}+{\underline {p}}}{2}},\sigma _{X}={\sqrt {Var[X]}}={\frac {\Delta p}{6}}}$

Сумма n нормально распределенных случайных величин является нормально распределенными случайными величинами со следующими характеристиками (см. Шесть сигм )

${\displaystyle E[nX]=n{\frac {{\overline {p}}+{\underline {p}}}{2}},\sigma _{nX}={\sqrt {nVar[X]}}={\sqrt {n}}\sigma ={\sqrt {n}}{\frac {\Delta p}{6}}}$

Можно предположить, что ширина вероятностного результата равна 6 сигм (сравните Шесть сигм ).

${\displaystyle 6\sigma _{nX}=6{\sqrt {n}}{\frac {\Delta p}{6}}={\sqrt {n}}\Delta p}$

Теперь мы можем сравнить ширину интервала результата и вероятностного результата.

${\displaystyle {\frac {width\ of\ n\ intervals}{width\ of\ n\ random\ variables}}={\frac {n\Delta p}{{\sqrt {n}}\Delta p}}={\sqrt {n}}}$

Из-за этого результаты интервального конечного элемента (или вообще анализа наихудшего случая) могут быть завышены по сравнению со стохастическим анализом бедренной кости (см. Также распространение неопределенности ). Однако в случае небезопасной неопределенности невозможно применить чисто вероятностные методы. Потому что вероятностные характеристики в этом случае точно не известны [ Elishakoff 2000].

Можно рассматривать случайные (и нечеткие случайные величины) с интервальными параметрами (например, со средним интервалом, дисперсией и т. Д.). Некоторые исследователи используют интервальные (нечеткие) измерения в статистических расчетах (например, [2] ). В результате таких вычислений мы получим так называемую неточную вероятность .

Неточная вероятность понимается в очень широком смысле. Он используется как общий термин для обозначения всех математических моделей, которые измеряют вероятность или неопределенность без точных числовых вероятностей. Он включает как качественные (сравнительная вероятность, частичное упорядочение предпочтений,…), так и количественные режимы (интервальные вероятности, функции убеждений, верхнее и нижнее предвидение,…). Неточные вероятностные модели необходимы в задачах вывода, когда релевантная информация недостаточна, расплывчата или противоречива, а также в задачах принятия решений, где предпочтения также могут быть неполными [3] .

Простой пример: моделирование растяжения, сжатия, деформации и напряжения) [ править ]

Пример 1-измерения [ править ]

В напряжении - сжатие проблемы, следующие уравнения показывают соотношение между перемещением ¯u и силами Р :

${\displaystyle {\frac {EA}{L}}u=P}$

где L - длина, A - площадь поперечного сечения, а E - модуль Юнга .

Если модуль Юнга и сила неопределенны, то

${\displaystyle E\in [{\underline {E}},{\overline {E}}],P\in [{\underline {P}},{\overline {P}}]}$

Чтобы найти верхнюю и нижнюю границы смещения u , вычислите следующие частные производные :

${\displaystyle {\frac {\partial u}{\partial E}}={\frac {-PL}{E^{2}A}}<0}$

${\displaystyle {\frac {\partial u}{\partial P}}={\frac {L}{EA}}>0}$

Рассчитайте экстремальные значения смещения следующим образом:

${\displaystyle {\underline {u}}=u({\overline {E}},{\underline {P}})={\frac {{\underline {P}}L}{{\overline {E}}A}}}$

${\displaystyle {\overline {u}}=u({\underline {E}},{\overline {P}})={\frac {{\overline {P}}L}{{\underline {E}}A}}}$

Рассчитайте деформацию по следующей формуле:

${\displaystyle \varepsilon ={\frac {1}{L}}u}$

Рассчитайте производную деформации, используя производную от перемещений:

${\displaystyle {\frac {\partial \varepsilon }{\partial E}}={\frac {1}{L}}{\frac {\partial u}{\partial E}}={\frac {-P}{E^{2}A}}<0}$

${\displaystyle {\frac {\partial \varepsilon }{\partial P}}={\frac {1}{L}}{\frac {\partial u}{\partial P}}={\frac {1}{EA}}>0}$

Рассчитайте экстремальные значения смещения следующим образом:

${\displaystyle {\underline {\varepsilon }}=\varepsilon ({\overline {E}},{\underline {P}})={\frac {\underline {P}}{{\overline {E}}A}}}$

${\displaystyle {\overline {\varepsilon }}=\varepsilon ({\underline {E}},{\overline {P}})={\frac {\overline {P}}{{\underline {E}}A}}}$

Также можно рассчитать предельные значения деформации, используя перемещения

${\displaystyle {\frac {\partial \varepsilon }{\partial u}}={\frac {1}{L}}>0}$

тогда

${\displaystyle {\underline {\varepsilon }}=\varepsilon ({\underline {u}})={\frac {\underline {P}}{{\overline {E}}A}}}$

${\displaystyle {\overline {\varepsilon }}=\varepsilon ({\overline {u}})={\frac {\overline {P}}{{\underline {E}}A}}}$

Та же методика может быть применена к стрессу.

${\displaystyle \sigma =E\varepsilon }$

тогда

${\displaystyle {\frac {\partial \sigma }{\partial E}}=\varepsilon +E{\frac {\partial \varepsilon }{\partial E}}=\varepsilon +E{\frac {1}{L}}{\frac {\partial u}{\partial E}}={\frac {P}{EA}}-{\frac {P}{EA}}=0}$

${\displaystyle {\frac {\partial \sigma }{\partial P}}=E{\frac {\partial \varepsilon }{\partial P}}=E{\frac {1}{L}}{\frac {\partial u}{\partial P}}={\frac {1}{A}}>0}$

и

${\displaystyle {\underline {\sigma }}=\sigma ({\underline {P}})={\frac {\underline {P}}{A}}}$

${\displaystyle {\overline {\sigma }}=\sigma ({\overline {P}})={\frac {\overline {P}}{A}}}$

Если рассматривать стресс как функцию напряжения, тогда

${\displaystyle {\frac {\partial \sigma }{\partial \varepsilon }}={\frac {\partial }{\partial \varepsilon }}(E\varepsilon )=E>0}$

тогда

${\displaystyle {\underline {\sigma }}=\sigma ({\underline {\varepsilon }})=E{\underline {\varepsilon }}={\frac {\underline {P}}{A}}}$

${\displaystyle {\overline {\sigma }}=\sigma ({\overline {\varepsilon }})=E{\overline {\varepsilon }}={\frac {\overline {P}}{A}}}$

Конструкция безопасна, если напряжение меньше заданного значения, т. Е.${\displaystyle \sigma }$${\displaystyle \sigma _{0}}$

${\displaystyle \sigma <\sigma _{0}}$

это условие верно, если

${\displaystyle {\overline {\sigma }}<\sigma _{0}}$

После расчета мы знаем, что это соотношение выполняется, если

${\displaystyle {\frac {\overline {P}}{A}}<\sigma _{0}}$

Пример очень простой, но он показывает применение интервальных параметров в механике. Интервальные МКЭ используют очень похожую методологию в многомерных случаях [Pownuk 2004].

Однако в многомерных случаях связь между неопределенными параметрами и решением не всегда бывает монотонной. В этом случае необходимо применять более сложные методы оптимизации. ^[1]

Многомерный пример [ править ]

В случае задачи растяжения- сжатия уравнение равновесия имеет следующий вид

${\displaystyle {\frac {d}{dx}}\left(EA{\frac {du}{dx}}\right)+n=0}$

где u - смещение, E - модуль Юнга , A - площадь поперечного сечения, а n - распределенная нагрузка. Чтобы получить уникальное решение, необходимо добавить соответствующие граничные условия, например

${\displaystyle u(0)=0}$

${\displaystyle {\frac {du(0)}{dx}}EA=P}$

Если модуль Юнга E и n неопределенны, то интервальное решение может быть определено следующим образом

${\displaystyle {\mathbf {u} }(x)=\left\{u(x):{\frac {d}{dx}}\left(EA{\frac {du}{dx}}\right)+n=0,u(0)=0,{\frac {du(0)}{dx}}EA=P,E\in [{\underline {E}},{\overline {E}}],P\in [{\underline {P}},{\overline {P}}]\right\}}$

Для каждого элемента МКЭ можно умножить уравнение на тестовую функцию v

${\displaystyle \int \limits _{0}^{L^{e}}\left({\frac {d}{dx}}\left(EA{\frac {du}{dx}}\right)+n\right)v=0}$

куда ${\displaystyle x\in [0,L^{(e)}].}$

После интегрирования по частям получим уравнение в слабой форме

${\displaystyle \int \limits _{0}^{L^{(e)}}EA{\frac {du}{dx}}{\frac {dv}{dx}}dx=\int \limits _{0}^{L^{(e)}}nvdx}$

куда ${\displaystyle x\in [0,L^{(e)}].}$

Давайте введем набор точек сетки , где - количество элементов, и функции линейной формы для каждого элемента FEM.${\displaystyle x_{0},x_{1},...,x_{Ne}}$${\displaystyle Ne}$

${\displaystyle N_{1}^{(e)}(x)=1-{\frac {1-x_{0}^{(e)}}{x_{1}^{(e)}-x_{0}^{(e)}}},\ \ N_{2}^{(e)}(x)={\frac {1-x_{0}^{(e)}}{x_{1}^{(e)}-x_{0}^{(e)}}}.}$

куда ${\displaystyle x\in [x_{0}^{(e)},x_{1}^{(e)}].}$

${\displaystyle x_{1}^{(e)}}$левая конечная точка элемента, левая конечная точка элемента с номером «е». Приближенное решение в "е" -м элементе представляет собой линейную комбинацию функций формы${\displaystyle x_{1}^{(e)}}$

${\displaystyle u_{h}^{(e)}(x)=u_{1}^{e}N_{1}^{(e)}(x)+u_{2}^{e}N_{2}^{(e)}(x),\ \ v_{h}^{(e)}(x)=u_{1}^{e}N_{1}^{(e)}(x)+u_{2}^{e}N_{2}^{(e)}(x)}$

После подстановки в слабую форму уравнения мы получим следующую систему уравнений

${\displaystyle \left[{\begin{array}{cc}{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}&-{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}\\-{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}&{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}\\\end{array}}\right]\left[{\begin{array}{c}u_{1}^{(e)}\\u_{2}^{(e)}\end{array}}\right]=\left[{\begin{array}{c}\int \limits _{0}^{L^{(e)}}nN_{1}^{(e)}(x)dx\\\int \limits _{0}^{L^{(e)}}nN_{2}^{(e)}(x)dx\end{array}}\right]}$

или в матричной форме

${\displaystyle K^{(e)}u^{(e)}=Q^{(e)}}$

Чтобы собрать глобальную матрицу жесткости, необходимо рассмотреть уравнения равновесия в каждом узле. После этого уравнение имеет следующий матричный вид

${\displaystyle Ku=Q}$

куда

${\displaystyle K=\left[{\begin{array}{ccccc}K_{11}^{(1)}&K_{12}^{(1)}&0&...&0\\K_{21}^{(1)}&K_{22}^{(1)}+K_{11}^{(2)}&K_{12}^{(2)}&...&0\\0&K_{21}^{(2)}&K_{22}^{(2)}+K_{11}^{(3)}&...&0\\...&...&...&...&...\\0&0&...&K_{22}^{(Ne-1)}+K_{11}^{(Ne)}&K_{11}^{(Ne)}\\0&0&...&K_{21}^{(Ne)}&K_{22}^{(Ne)}\end{array}}\right]}$

- глобальная матрица жесткости,

${\displaystyle u=\left[{\begin{array}{c}u_{0}\\u_{1}\\...\\u_{Ne}\\\end{array}}\right]}$

- вектор решения,

${\displaystyle Q=\left[{\begin{array}{c}Q_{0}\\Q_{1}\\...\\Q_{Ne}\\\end{array}}\right]}$

это правая часть.

В случае проблемы растяжения-сжатия

${\displaystyle K=\left[{\begin{array}{ccccc}{\frac {E^{(1)}A^{(1)}}{L^{(1)}}}&-{\frac {E^{(1)}A^{(1)}}{L^{(1)}}}&0&...&0\\-{\frac {E^{(1)}A^{(1)}}{L^{(1)}}}&{\frac {E^{(1)}A^{(1)}}{L^{(1)}}}+{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}&-{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}&...&0\\0&-{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}&{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}+{\frac {E^{(3)}A^{(3)}}{L^{(3)}}}&...&0\\...&...&...&...&...\\0&0&...&{\frac {E^{(Ne-1)}A^{(Ne-1)}}{L^{(Ne-1)}}}+{\frac {E^{(Ne)}A^{(Ne)}}{L^{(Ne)}}}&-{\frac {E^{(Ne)}A^{(Ne)}}{L^{(Ne)}}}\\0&0&...&-{\frac {E^{(Ne)}A^{(Ne)}}{L^{(Ne)}}}&{\frac {E^{(Ne)}A^{(Ne)}}{L^{(Ne)}}}\end{array}}\right]}$

Если пренебречь распределенной нагрузкой n

${\displaystyle Q=\left[{\begin{array}{c}R\\0\\...\\0\\P\\\end{array}}\right]}$

После учета граничных условий матрица жесткости имеет следующий вид

${\displaystyle K=\left[{\begin{array}{ccccc}1&0&0&...&0\\0&{\frac {E^{(1)}A^{(1)}}{L^{(1)}}}+{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}&-{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}&...&0\\0&-{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}&{\frac {E^{(2)}A^{(2)}}{L^{(2)}}}+{\frac {E^{(3)}A^{(3)}}{L^{(3)}}}&...&0\\...&...&...&...&...\\0&0&...&{\frac {E^{(e-1)}A^{(e-1)}}{L^{(e-1)}}}+{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}&-{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}\\0&0&...&-{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}&{\frac {E^{(e)}A^{(e)}}{L^{(e)}}}\end{array}}\right]=K(E,A)=K(E^{(1)},...,E^{(Ne)},A^{(1)},...,A^{(Ne)})}$

Правая часть имеет следующий вид

${\displaystyle Q=\left[{\begin{array}{c}0\\0\\...\\0\\P\\\end{array}}\right]=Q(P)}$

Предположим, что модуль Юнга E , площадь поперечного сечения A и нагрузка P неопределенны и принадлежат некоторым интервалам

${\displaystyle E^{(e)}\in [{\underline {E}}^{(e)},{\overline {E}}^{(e)}]}$

${\displaystyle A^{(e)}\in [{\underline {A}}^{(e)},{\overline {A}}^{(e)}]}$

${\displaystyle P\in [{\underline {P}},{\overline {P}}]}$

Интервальное решение можно определить вычислением следующим образом

${\displaystyle {\mathbf {u} }=\lozenge \{u:K(E,A)u=Q(P),E^{(e)}\in [{\underline {E}}^{(e)},{\overline {E}}^{(e)}],A^{(e)}\in [{\underline {A}}^{(e)},{\overline {A}}^{(e)}],P\in [{\underline {P}},{\overline {P}}]\}}$

Вычисление интервального вектора в целом NP-сложно , однако в определенных случаях можно вычислить решение, которое может использоваться во многих инженерных приложениях.${\displaystyle {\mathbf {u} }}$

Результатом расчетов являются интервальные смещения

${\displaystyle u_{i}\in [{\underline {u}}_{i},{\overline {u}}_{i}]}$

Предположим, что смещения в столбце должны быть меньше некоторого заданного значения (из соображений безопасности).

${\displaystyle u_{i}<u_{i}^{\max }}$

Неопределенная система безопасна, если интервальное решение удовлетворяет всем условиям безопасности.

В данном конкретном случае

${\displaystyle u_{i}<u_{i}^{\max },\ \ \ u_{i}\in [{\underline {u}}_{i},{\overline {u}}_{i}]}$

или просто

${\displaystyle {\overline {u}}_{i}<u_{i}^{\max }}$

При постобработке можно рассчитать интервальное напряжение, интервальную деформацию и функции предельного состояния интервала и использовать эти значения в процессе проектирования.

Метод интервальных конечных элементов может применяться для решения задач, в которых недостаточно информации для создания надежных вероятностных характеристик конструкций [ Elishakoff 2000]. Метод интервальных конечных элементов также может применяться в теории неточной вероятности .

Метод комбинирования конечных точек [ править ]

Можно решить уравнение для всех возможных комбинаций конечных точек интервала . Список всех вершин интервала можно записать как . Верхнюю и нижнюю границы решения можно вычислить следующим образом${\displaystyle K(p)u(p)=Q(p)}$${\displaystyle {\hat {p}}}$
${\displaystyle {\hat {p}}}$${\displaystyle L=\{p_{1}^{*},...,p_{n}^{*}\}}$

${\displaystyle {\underline {u}}_{i}=\min\{u_{i}(p_{k}^{*}):K(p_{k}^{*})u(p_{k}^{*})=Q(p_{k}^{*}),p_{k}^{*}\in L\}}$

${\displaystyle {\overline {u}}_{i}=\max\{u_{i}(p_{k}^{*}):K(p_{k}^{*})u(p_{k}^{*})=Q(p_{k}^{*}),p_{k}^{*}\in L\}}$

Метод комбинирования конечных точек дает решение, которое обычно бывает точным; к сожалению, этот метод имеет экспоненциальную вычислительную сложность и не может быть применен к задачам со многими интервальными параметрами [Neumaier 1990].

Метод расширения Тейлора [ править ]

Функцию можно расширить с помощью ряда Тейлора . В простейшем случае ряды Тейлора используют только линейное приближение${\displaystyle u=u(p)}$

${\displaystyle u_{i}(p)\approx u_{i}(p_{0})+\sum _{j}{\frac {\partial u(p_{0})}{\partial p_{j}}}\Delta p_{j}}$

Верхняя и нижняя границы решения могут быть рассчитаны по следующей формуле

${\displaystyle {\underline {u}}_{i}\approx u_{i}(p_{0})-\left|\sum _{j}{\frac {\partial u(p_{0})}{\partial p_{j}}}\right|\Delta p_{j}}$

${\displaystyle {\overline {u}}_{i}\approx u_{i}(p_{0})+\left|\sum _{j}{\frac {\partial u(p_{0})}{\partial p_{j}}}\right|\Delta p_{j}}$

Метод очень эффективен, но не очень точен.
Для повышения точности можно применить разложение Тейлора более высокого порядка [Pownuk 2004].
Этот подход может быть применен в интервале метода конечных разностей и интервального метода граничных элементов .

Метод градиента [ править ]

Если знак производных постоянен, то функции монотонны, и точное решение может быть вычислено очень быстро.${\displaystyle {\frac {\partial u_{i}}{\partial p_{j}}}}$${\displaystyle u_{i}=u_{i}(p)}$

если тогда${\displaystyle {\frac {\partial u_{i}}{\partial p_{j}}}\geq 0}$${\displaystyle p_{i}^{\min }={\underline {p}}_{i},\ p_{i}^{\max }={\overline {p}}_{i}}$

если тогда${\displaystyle {\frac {\partial u_{i}}{\partial p_{j}}}<0}$${\displaystyle p_{i}^{\min }={\overline {p}}_{i},\ p_{i}^{\max }={\underline {p}}_{i}}$

Экстремальные значения решения можно рассчитать следующим образом

${\displaystyle {\underline {u}}_{i}=u_{i}(p^{\min }),\ {\overline {u}}_{i}=u_{i}(p^{\max })}$

Во многих конструкторских приложениях этот метод дает точное решение.
Если решение не монотонное, оно обычно является разумным. Для повышения точности метода можно применять тесты на монотонность и анализ чувствительности более высокого порядка. Метод может быть применен для решения линейных и нелинейных задач вычислительной механики [Pownuk 2004]. Применение метода анализа чувствительности к решению задач гражданского строительства можно найти в следующей статье [М.В. Рама Рао, А. Павнук и И. Скална, 2008].
Этот подход может быть применен в интервале метода конечных разностей и интервального метода граничных элементов .

Элемент за методом элемента [ править ]

Муханна и Маллен применили поэлементную формулировку к решению уравнения конечных элементов с интервальными параметрами [Muhanna, Mullen 2001]. Используя этот метод, можно получить решение с гарантированной точностью в случае стропильных и каркасных конструкций.

Методы возмущения [ править ]

Матрица жесткости решения и вектор нагрузки могут быть расширены с помощью теории возмущений . Теория возмущений приводит к приближенному значению интервального решения [Qiu, Elishakoff 1998]. Метод очень эффективен и может быть применен к большим задачам вычислительной механики.${\displaystyle u=u(p)}$ ${\displaystyle K=K(p)}$${\displaystyle Q=Q(p)}$

Метод поверхности отклика [ править ]

Решение можно аппроксимировать , используя поверхность отклика . Затем можно использовать поверхность отклика для получения интервального решения [Akpan 2000]. Используя метод поверхности отклика, можно решить очень сложную задачу вычислительной механики [Beer 2008].${\displaystyle u=u(p)}$

Чистые интервальные методы [ править ]

Некоторые авторы пытались применить чисто интервальные методы к решению задач конечных элементов с интервальными параметрами. В некоторых случаях можно получить очень интересные результаты, например [Попова, Янков, Бонев 2008]. Однако в целом метод дает очень завышенные результаты [Kulpa, Pownuk, Skalna 1998].

Параметрические интервальные системы [ править ]

[Popova 2001] и [Skalna 2006] ввели методы решения системы линейных уравнений, в которой коэффициенты являются линейными комбинациями интервальных параметров. В этом случае можно получить очень точное решение интервальных уравнений с гарантированной точностью.

См. Также [ править ]

• Метод интервальных граничных элементов
• Интервал (математика)
• Интервальная арифметика
• Неточная вероятность
• Многозначная функция
• Дифференциальное включение
• Ошибка наблюдения
• Случайный компакт
• Надежность (статистика)
• Доверительный интервал
• Лучший, худший и средний случай
• Вероятностный дизайн
• Распространение неопределенности
• Экспериментальный анализ неопределенности
• Анализ чувствительности
• Теория возмущений
• Механика сплошной среды
• Механика твердого тела
• Ферма
• Космическая рамка
• Линейная эластичность
• Сопротивление материалов

Ссылки [ править ]

• У. О. Акпан, Т. С. Коко, И. Р. Орисамолу, Б. К. Галлант, Практический нечеткий анализ конструкций методом конечных элементов, Конечные элементы в анализе и проектировании, 38, стр. 93–111, 2000.
• М. Бир, Оценка несовместимых инженерных данных, Третий семинар по надежным инженерным вычислениям (REC08) Технологический институт Джорджии, 20–22 февраля 2008 г., Саванна, Джорджия, США.
• Демпстер, AP (1967). «Верхняя и нижняя вероятности, индуцированные многозначным отображением». Анналы математической статистики 38 (2): 325-339. [4] . Проверено 23 сентября 2009 г.
• Анализ неопределенности в гражданском строительстве, В. Феллин, Х. Лессманн, М. Обергуггенбергер и Р. Вайдер (ред.), Springer-Verlag, Берлин, 2005 г.
• Елишаков И. Возможные ограничения вероятностных методов в технике. Обзоры прикладной механики, Том 53, № 2, стр. 19–25, 2000 г.
• Главачек, И., Хлебоун, Дж., Бабушка, И.: Проблемы с неопределенными входными данными и метод наихудшего сценария. Эльзевир, Амстердам (2004)
• Кёйлюоглу, У., Исаак Елишаков ; Сравнение стохастических и интервальных конечных элементов, применяемых к каркасам сдвига с неопределенными свойствами жесткости, Computers & Structures Volume: 67, Issue: 1-3, April 1, 1998, pp. 91–98
• Кульпа З. , Павнюк А., Скална И., Анализ линейных механических конструкций с неопределенностями с помощью интервальных методов. Компьютерная механика и инженерные науки, т. 5. 1998. С. 443–477.
• Д. Моенс и Д. Вандепитт, Теория интервальной чувствительности и ее применение к анализу огибающей частотной характеристики неопределенных структур. Компьютерные методы в прикладной механике и технике Vol. 196, № 21-24, 1 апреля 2007 г., стр. 2486–2496.
• Мёллер Б., Бир М. Нечеткая случайность - неопределенность в гражданском строительстве и вычислительной механике. Издательство Springer, Берлин, 2004.
• Р.Л. Муханна, Р.Л. Маллен, Неопределенность в задачах механики - интервальный подход. Журнал инженерной механики, Том 127, №6, 2001 г., 557-556
• А. Ноймайер, Интервальные методы для систем уравнений, Cambridge University Press, Нью-Йорк, 1990.
• Попова Е. О решении параметризованных линейных систем. В. Кремер, Дж. Вольф фон Гуденберг (редакторы): научные вычисления, проверенные числа, интервальные методы. Kluwer Acad. Издательство, 2001, с. 127–138.
• Е. Попова, Р. Янков, З. Бонев: Ограничение отклика механических конструкций с неопределенностями по всем параметрам. В RLMuhannah, RLMullen (Eds): Proceedings of the NSF Workshop on Reliable Engineering Computing (REC), Svannah, Georgia USA, 22-24 февраля 2006 г., 245-265
• A. Pownuk, Численные решения нечетких дифференциальных уравнений в частных производных и их применение в вычислительной механике, Нечеткие дифференциальные уравнения с частными производными и реляционные уравнения: характеристика и моделирование коллектора (М. Никравеш, Л. Заде и В. Коротких, ред.), Исследования в области нечеткости и мягкие вычисления, Physica-Verlag, 2004, стр. 308–347.
• A. Pownuk, Эффективный метод решения крупномасштабных инженерных задач с интервальными параметрами на основе анализа чувствительности, Материалы семинара NSF по надежным инженерным вычислениям, 15–17 сентября 2004 г., Саванна, Джорджия, США, стр. 305–316
• М. В. Рама Рао, А. Павунук и И. Скална, Расчет напряжений в монолитной железобетонной балке с неопределенными структурными параметрами, Семинар NSF по надежным инженерным вычислениям, 20–22 февраля 2008 г., Саванна, Джорджия, США, стр. 459–478
• И. Скална, Метод внешнего интервального решения систем линейных уравнений, линейно зависящих от интервальных параметров, Надежные вычисления, Том 12, номер 2, апрель, 2006 г., стр. 107–120
• З. Цю и И. Элишаков , Антиоптимизация конструкций с большими неопределенными, но неслучайными параметрами с помощью интервального анализа Компьютерные методы в прикладной механике и технике, Том 152, выпуски 3-4, 24 января 1998 г., страницы 361-372
• Бернардини, Альберто, Тонон, Фульвио, Граничная неопределенность в гражданском строительстве, Springer 2010

• Бен-Хаим Ю., Элишаков И. , 1990, Выпуклые модели неопределенности в прикладной механике. Издательство Elsevier Science, Нью-Йорк

• Валлиаппан С., Фам Т.Д., 1993, Нечеткий конечно-элементный анализ фундамента на упругом грунте. Международный журнал численных и аналитических методов в геомеханике, том 17, стр. 771–789

• Элишаков И. , Ли Ю. В. , Старнес Дж. Х., 1994, Детерминированный метод прогнозирования влияния неизвестных, но ограниченных модулей упругости на изгиб композитных конструкций. Компьютерные методы в прикладной механике и технике, Том 111, с. 155–167.

• Валлиаппан С. Фам Т.Д., 1995, Анализ конечных элементов упругопластических элементов с нечеткими параметрами. Международный журнал численных методов в инженерии, 38, стр. 531–548.

• Рао С.С., Сойер Дж. П., 1995, Нечеткий метод конечных элементов для анализа неточно определенных систем. Журнал AIAA, Том 33, № 12, стр. 2364–2370

• Köylüoglu HU, Cakmak A., Nielsen SRK, 1995, Отображение интервалов в строительной механике. В кн .: Спанос, под ред. Вычислительная стохастическая механика. 125-133. Балкема, Роттердам

• Муханна, Р.Л. и Р.Л. Маллен (1995). "Разработка интервальных методов для нечеткости в механике сплошной среды" в материалах 3-го Международного симпозиума по моделированию и анализу неопределенности и ежегодной конференции Североамериканского общества обработки нечеткой информации (ISUMA – NAFIPS'95), IEEE, 705–710

Внешние ссылки [ править ]

• Надежные инженерные вычисления, Технологический институт Джорджии, Саванна, США
• Интервальные вычисления
• Надежные вычисления (журнал)
• Интервальные уравнения (сборники ссылок)
• Веб-приложения с интервалом конечных элементов
• Попова Е. А. Набор параметрических решений интервальной линейной системы.
• Общество неточной вероятности: теории и приложения