Эта статья включает в себя список общих ссылок , но он остается в основном непроверенным, поскольку в нем отсутствуют соответствующие встроенные ссылки . ( Июль 2014 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения ) |
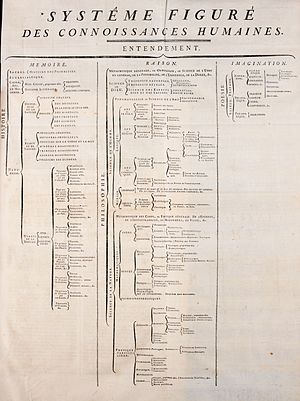
Структура дерева или древовидная схема представляет собой способ представления иерархической природы структуры в графической форме. Это называется «древовидной структурой», потому что классическое представление напоминает дерево , хотя диаграмма обычно перевернута по сравнению с биологическим деревом, со «стволом» вверху и «листьями» внизу.
Древовидная структура концептуальна и представлена в нескольких формах. Для обсуждения древовидных структур в определенных областях см. Дерево (структура данных) для информатики: насколько это относится к теории графов, см. Дерево (теория графов) или также дерево (теория множеств) . Перечислены другие статьи по теме.
Терминология и свойства [ править ]
Элементы дерева называются « узлами ». Линии, соединяющие элементы, называются «ветвями». Узлы без дочерних узлов называются листовыми узлами , «конечными узлами» или «листьями».
Каждая конечная древовидная структура имеет член, у которого нет старшего . Этот член называется «корневым» или корневым узлом . Корень - это начальный узел. Но обратное неверно: бесконечные древовидные структуры могут иметь или не иметь корневой узел.
Имена отношений между узлами моделируют родственную терминологию семейных отношений. Гендерно-нейтральные имена «родитель» и «ребенок» в значительной степени вытеснили старые термины «отец» и «сын». Термин «дядя» по-прежнему широко используется для других узлов на том же уровне, что и родительский, хотя иногда его заменяют нейтральными с гендерной точки зрения терминами, такими как «оммер». [1]
- «Родитель» узла - это узел на одну ступень выше в иерархии (т. Е. Ближе к корневому узлу) и лежащий на той же ветви.
- «Родственные» («брат» или «сестра») узлы совместно используют один и тот же родительский узел.
- «Дяди» узла (иногда «оммеры») являются братьями и сестрами родительского узла.
- Узел, который связан со всеми узлами нижнего уровня, называется «предком». Подключенные узлы нижнего уровня являются «потомками» узла-предка.
В данном примере «энциклопедия» является родоначальником «науки» и «культуры», своих детей. «Искусство» и «ремесло» - это братья и сестры и дети «культуры», которая является их родителем и, следовательно, одним из их предков. Кроме того, «энциклопедия», как корень дерева, является прародительницей «науки», «культуры», «искусства» и «ремесла». Наконец, «наука», «искусство» и «ремесло», как листья, не являются предками ни одного другого узла.
Древовидные структуры могут отображать все виды таксономических знаний, такие как родословные , биологическое эволюционное древо , эволюционное дерево языковой семьи , грамматическая структура языка (ключевой пример - S → NP VP, что означает, что предложение является существительным фраза и глагольная фраза, каждый из которых, в свою очередь, имеет другие компоненты, которые имеют другие компоненты), способ логического упорядочения веб-страниц на веб-сайте, математические деревья целочисленных множеств и т. д.
В Оксфордский словарь английского языка записи использование как термины «структура дерева» и «дерево-схема» с 1965 по Ноам Хомский «s Аспекты теории синтаксиса . [2]
В древовидной структуре существует один и только один путь из любой точки в любую другую точку.
Информатика широко использует древовидные структуры ( см. Дерево (структура данных) и телекоммуникации ).
Для формального определения см. Теорию множеств , а для обобщения, в котором дети не обязательно являются преемниками, см. Порядок префиксов .
Примеры древовидной структуры [ править ]
- Интернет:
- иерархия usenet
- Вакуумные трубки
- Логическая структура объектной модели документа [3] Yahoo! предметный указатель, Curlie
- Операционная система : структура каталогов
- Управление информацией: десятичная система Дьюи , PSH , этот иерархический маркированный список
- Управление: иерархические организационные структуры
- Информатика:
- двоичное дерево поиска
- красно-черное дерево
- AVL дерево
- R-дерево
- Биология: эволюционное древо
- Бизнес: пирамида схема продаж
- Управление проектом: декомпозиционная структура работ
- Лингвистика:
- (Синтаксис) Деревья структуры фраз
- (Историческая лингвистика) Древовидная модель языковых изменений
- Спорт: деловые шахматы , сетка плей-офф
- Математика: Вселенная фон Неймана
- Теория групп: деревья потомков
Представление деревьев [ править ]
Есть много способов визуального представления древовидной структуры. Почти всегда они сводятся к вариациям или комбинациям нескольких основных стилей:
Классические диаграммы узловых связей [ править ]
Классические схемы узловых соединений, которые соединяют узлы вместе с отрезками линий:
| энциклопедия | ||
|---|---|---|
| / культура | \ наука | |
| / искусство | \ ремесло | |
Вложенные наборы [ править ]
Вложенные наборы, которые используют вложение / включение для демонстрации отцовства, примеры включают TreeMaps и фрактальные карты :
| энциклопедия | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||
Многослойные диаграммы "сосульки" [ править ]
Многослойные диаграммы «сосульки», использующие выравнивание / смежность.
| энциклопедия | ||
|---|---|---|
| культура | наука | |
| Изобразительное искусство | ремесло | |
Контуры и виды дерева [ править ]
Списки или диаграммы, в которых используется отступ, иногда называемый « контурами » или « древовидными представлениями ».
Схема:
- энциклопедия
- культура
- Изобразительное искусство
- ремесло
- наука
- культура
Древовидный вид:
- энциклопедия
- культура
- Изобразительное искусство
- ремесло
- наука
- культура
Вложенные круглые скобки [ править ]
Соответствие вложенным скобкам впервые заметил сэр Артур Кэли :
((искусство, ремесло) культура, наука) энциклопедия
или
энциклопедия (культура (искусство, ремесло), наука)
Радиальные деревья [ править ]
Деревья также могут быть представлены радиально :
| искусство \ | ремесло / |
|---|---|
| культура | | |
| энциклопедия | |
| | наука | |
См. Также [ править ]
- Виды деревьев
- B-дерево
- Танцующее дерево
- Древо решений
- Двоичное дерево левого потомка и правого брата
- Дерево (структура данных)
- Дерево (теория графов)
- Дерево (теория множеств)
- Статьи по Теме
- Бурение данных
- Иерархическая модель : кластеризация и запрос
- Тестирование деревьев
Ссылки [ править ]
- ^ «Глоссарий Ethereum» . GitHub . Проверено 17 апреля 2019 года .
- ^ "дерево" . Оксфордский словарь английского языка (Интернет-изд.). Издательство Оксфордского университета. (Требуется подписка или членство в учреждении-участнике .)
- ^ "Что такое объектная модель документа?" . Домен архитектуры W3C . Проверено 5 декабря 2006 .
Дальнейшее чтение [ править ]
Идентификацию некоторых основных стилей древовидной структуры можно найти в:
- Жак Бертин , Семиология графики , 1983, University of Wisconsin Press (2-е издание, 1973, ISBN 978-0299090609 ;
- Дональд Э. Кнут , Искусство программирования , Том I: Фундаментальные алгоритмы, 1968, Addison-Wesley, стр. 309–310;
- Брайан Джонсон и Бен Шнейдерман , Древовидные карты: подход к визуализации иерархических информационных структур , заполняющий пространство , в Proceedings of IEEE Visualization (VIS), 1991, стр. 284–291, ISBN 0-8186-2245-8 ;
- Питер Идс , Тао Линь и Сюэминь Линь, Две схемы рисования деревьев , Международный журнал вычислительной геометрии и приложений, 1993, том 3, номер 2, стр. 133–153.
- Мануэль Лима , Книга деревьев: визуализация ветвей знания (2014), Princeton Architectural Press , ISBN 978-1-616-89218-0
Внешние ссылки [ править ]
| Викискладе есть медиафайлы по теме древовидной диаграммы . |
- Визуализация филогенетических деревьев на сервере T-REX
- Использование древовидной структуры для разработки бизнес-процесса - от Общества технических коммуникаций