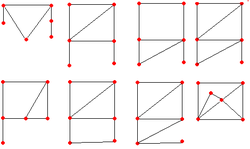
В теории графов , разделе математики, неориентированный граф называется асимметричным графом, если он не имеет нетривиальных симметрий.
Формально автоморфизм графа - это перестановка p его вершин со свойством, что любые две вершины u и v смежны тогда и только тогда, когда p ( u ) и p ( v ) смежны. Тождественное отображение графа на себя всегда автоморфизм, и называется тривиальный автоморфизм графа. Асимметричный граф - это граф, для которого нет других автоморфизмов.
Примеры [ править ]
Наименьшие несимметричные нетривиальные графы имеют 6 вершин. [1] Наименьшие асимметричные регулярные графы имеют десять вершин; существуют асимметричные графы с десятью вершинами, которые являются 4-регулярными и 5-регулярными. [2] [3] Один из пяти самых маленьких асимметричных кубических графов [4] - это двенадцатигранный граф Фрухта, открытый в 1939 году. [5] Согласно усиленной версии теоремы Фрухта существует бесконечно много асимметричных кубических графов.
Свойства [ править ]
Класс асимметричных графов замкнут относительно дополнений : граф G асимметричен тогда и только тогда, когда его дополнение есть. [1] Любой асимметричный граф с n вершинами можно сделать симметричным, добавляя и удаляя в общей сложности не более n / 2 + o ( n ) ребер. [1]
Случайные графики [ править ]
Доля графов на n вершинах с нетривиальным автоморфизмом стремится к нулю с ростом n , что неформально выражается как « почти все конечные графы асимметричны». Напротив, опять же неформально, «почти все бесконечные графы симметричны». В частности, счетные бесконечные случайные графы в модели Эрдеша – Реньи с вероятностью 1 изоморфны высокосимметричному графу Радо . [1]
Деревья [ править ]
Наименьшее асимметричное дерево имеет семь вершин: оно состоит из трех путей длиной 1, 2 и 3, связанных в общей конечной точке. [6] В отличие от графов, почти все деревья симметричны. В частности, если дерево выбирается равномерно случайным образом среди всех деревьев на n помеченных узлах, то с вероятностью, стремящейся к 1 при увеличении n , дерево будет содержать два листа, смежных с одним и тем же узлом, и будет иметь симметрии, заменяющие эти два листа. [1]
Ссылки [ править ]
- ^ a b c d e Erdős, P .; Реньи, А. (1963), "Асимметричные графы" (PDF) , Acta Mathematica Hungarica , 14 (3): 295-315, DOI : 10.1007 / BF01895716 , архивируются от оригинала (PDF) на 2017-07-06 , извлекаться 2010-04-22.
- ^ Барон, G .; Имрих, В. (1969), "Asymmetrische reguläre графена", Acta Mathematica Academiae Scientiarum Hungaricae , 20 : 135-142, DOI : 10.1007 / BF01894574 , МР 0238726 .
- ^ Гевиртц, Аллан; Хилл, Энтони; Квинтас, Луи В. (1969), "Минимальное количество точек для регулярных асимметричных графов", Universidad Técnica Federico Santa Maria. Scientia , 138 : 103–111, MR 0266818 .
- ^ Буссемейкер, ФК; Cobeljic, S .; Цветкович, DM; Зайдель, Дж. Дж. (1976), Компьютерное исследование кубических графов , отчет EUT, 76-WSK-01, кафедра математики и вычислительной техники, Технологический университет Эйндховена
- ^ Frucht, R. (1939), "Herstellung фон графена мит vorgegebener abstrakter Gruppe." , Compositio Mathematica (на немецком языке), 6 : 239–250, ISSN 0010-437X , Zbl 0020.07804 CS1 maint: обескураженный параметр ( ссылка ).
- ^ Квинтас Луи В. (1967), "экстремумы относительно асимметричных графов", Журнал комбинаторной теории , 3 (1): 57-82, DOI : 10.1016 / S0021-9800 (67) 80018-8.
| Викискладе есть медиафайлы, связанные с асимметричными графами . |