| Дерево двоичного поиска | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | дерево | ||||||||||||||||||||
| Изобрел | 1960 г. | ||||||||||||||||||||
| Изобретенный | П.Ф. Виндли, А.Д. Бут , А.Дж.Т. Колин и Т.Н. Хиббард | ||||||||||||||||||||
| Сложность времени в большой нотации O | |||||||||||||||||||||
| |||||||||||||||||||||
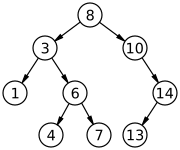
В информатике , бинарное дерево поиска ( BST ), также называется упорядоченный или сортируется бинарное дерево , это коренится бинарное дерево , чьи внутренние узлы каждый магазин ключ больше всех ключей в левом поддереве узла и меньше , чем в своем праве поддерево. Двоичное дерево - это тип структуры данных для хранения данных, таких как числа, в организованном порядке. Деревья двоичного поиска позволяют выполнять двоичный поиск для быстрого поиска, добавления и удаления элементов данных и могут использоваться для реализации динамических наборов и таблиц поиска.. Порядок узлов в BST означает , что каждое сравнение пропускает около половины оставшегося дерева, так что весь поиск занимает время , пропорциональное в двоичном логарифм числа элементов , хранящихся в дереве. Это намного лучше, чем линейное время, необходимое для поиска элементов по ключу в (несортированном) массиве, но медленнее, чем соответствующие операции с хеш-таблицами . Было изучено несколько вариантов бинарного дерева поиска.
Определение [ править ]
Двоичное дерево поиска - это двоичное дерево с корневым элементом , каждый внутренний узел которого хранит ключ (и, необязательно, связанное значение), и каждый имеет два выделенных поддерева, обычно обозначаемых левым и правым . Дерево дополнительно удовлетворяет свойству двоичного поиска : ключ в каждом узле больше или равен любому ключу, хранящемуся в левом поддереве, и меньше или равен любому ключу, хранящемуся в правом поддереве. [1] : 287 Листья (конечные узлы) дерева не содержат ключей и не имеют структуры, позволяющей отличать их друг от друга.
Часто информация, представленная каждым узлом, представляет собой запись, а не отдельный элемент данных. Однако в целях упорядочения узлы сравниваются по их ключам, а не по какой-либо части связанных с ними записей. Основное преимущество бинарных деревьев поиска по сравнению с другими структурами данных является то , что соответствующие алгоритмы сортировки и поиска алгоритмов , таких как упорядоченную обхода может быть очень эффективным.
Деревья двоичного поиска - это фундаментальная структура данных, используемая для создания более абстрактных структур данных, таких как наборы , мультимножества и ассоциативные массивы .
- При вставке или поиске элемента в двоичном дереве поиска ключ каждого посещенного узла должен сравниваться с ключом элемента, который будет вставлен или найден.
- Форма двоичного дерева поиска полностью зависит от порядка вставок и удалений и может стать вырожденной.
- После длинной смешанной последовательности случайных вставок и удалений ожидаемая высота дерева приближается к квадратному корню из числа ключей, √ n , [ цитата необходима ], которая растет намного быстрее, чем log n .
- Было проведено много исследований, чтобы предотвратить вырождение дерева, приводящее к наихудшей временной сложности O ( n ) (подробности см. В разделе Типы ).
Отношение заказа [ править ]
Двоичный поиск требует отношения порядка, с помощью которого каждый элемент (элемент) может сравниваться с любым другим элементом в смысле общего предварительного заказа . Часть элемента, которая эффективно участвует в сравнении, называется его ключом . Будь то дубликаты, т.е. е. разные элементы с одним и тем же ключом, должны быть разрешены в дереве или нет, не зависит от отношения порядка, а только от приложения. Информацию о функции поиска, поддерживающей и обрабатывающей дубликаты в дереве, см. В разделе Разрешенный поиск дубликатов .
В контексте бинарных деревьев поиска общий предварительный заказ наиболее гибко реализуется с помощью подпрограммы трехстороннего сравнения .
Операции [ править ]
Деревья двоичного поиска поддерживают три основные операции: вставку элементов, удаление элементов и поиск (проверка наличия ключа).
Поиск [ править ]
Поиск в двоичном дереве поиска определенного ключа может быть запрограммирован рекурсивно или итеративно .
Начнем с изучения корневого узла . Если дерево пустое , ключ, который мы ищем, не существует в дереве. В противном случае, если ключ равен ключу корня, поиск будет успешным и мы вернем узел. Если ключ меньше, чем у корня, мы ищем левое поддерево. Точно так же, если ключ больше, чем у корня, мы ищем правое поддерево. Этот процесс повторяется до тех пор, пока ключ не будет найден или оставшееся поддерево не станет нулевым . Если искомый ключ не найден после достижения нулевого поддерева, значит, этот ключ отсутствует в дереве. Это легко выразить в виде рекурсивного алгоритма (реализованного на Python ):
def search_recursively ( ключ , узел ): если node == None или node . ключ == ключ : узел возврата если ключ < узел . ключ : вернуться search_recursively ( ключ , узел . слева ) если ключ > узел . ключ : вернуться search_recursively ( ключ , узел . право )Этот же алгоритм можно реализовать итеративно:
def search_iteratively ( ключ , узел ): current_node = узел в то время как current_node ! = Нет : если ключ == current_node . ключ : вернуть current_node если ключ < current_node . ключ : current_node = текущий_узел . оставили иначе : # ключ> current_node.key: current_node = текущий_узел . верно вернуть current_nodeЭти два примера не поддерживают дублирование, то есть они считают дерево полностью упорядоченным.
Можно отметить, что рекурсивный алгоритм хвостовой рекурсивный . На языке, поддерживающем оптимизацию хвостового вызова, рекурсивные и итеративные примеры будут компилироваться в эквивалентные программы.
Поскольку в худшем случае этот алгоритм должен искать от корня дерева до листа, наиболее удаленного от корня, операция поиска занимает время, пропорциональное высоте дерева (см. Терминологию дерева ). В среднем деревья двоичного поиска с ключами узлов имеют высоту O (журнал | Узлы |) . [примечание 1] Однако в худшем случае деревья двоичного поиска могут иметь высоту O (| Узлы |) , когда несбалансированное дерево напоминает связанный список ( вырожденное дерево ).
Разрешен поиск с дубликатами [ править ]
Если отношение порядка является только полным предварительным порядком, разумным расширением функциональности является следующее: также в случае поиска равенства до конечных точек. Таким образом, позволяя указать (или жестко привязать) направление, в котором следует вставить дубликат, справа или слева от всех дубликатов в дереве на данный момент. Если направление жестко задано, оба варианта, правый и левый, поддерживают стек с вставкой дубликата в качестве операции выталкивания и удалением в качестве операции выталкивания. [2] : 155
def search_duplicatesAllowed ( ключ , узел ): current_node = узел в то время как current_node ! = Нет : если ключ < current_node . ключ : current_node = текущий_узел . оставили иначе : # ключ> = current_node.key: current_node = текущий_узел . верно вернуть current_nodeБинарное дерево рода , оборудованное такой функция поиска становится стабильным .
Вставка [ править ]
Вставка начинается так же, как и поиск; если ключ не совпадает с ключом корня, мы ищем левое или правое поддерево, как и раньше. В конце концов, мы достигнем внешнего узла и добавим новую пару «ключ-значение» (здесь закодирована как запись «newNode») в качестве его правого или левого дочернего элемента, в зависимости от ключа узла. Другими словами, мы исследуем корень и рекурсивно вставляем новый узел в левое поддерево, если его ключ меньше ключа корня, или в правое поддерево, если его ключ больше или равен корню.
Вот как может выполняться типичная вставка двоичного дерева поиска в двоичное дерево в C ++ :
void insert ( Node * & root , int key , int value ) { if ( ! root ) root = new Node ( key , value ); иначе, если ( ключ == корень -> ключ ) корень -> значение = значение ; иначе, если ( ключ < корень -> ключ ) вставить ( корень-> слева , ключ , значение ); else // ключ> корень-> вставка ключа ( корень -> вправо , ключ , значение ); }В качестве альтернативы, нерекурсивная версия может быть реализована таким образом. Использование указателя на указатель для отслеживания того, откуда мы пришли, позволяет коду избежать явной проверки и обработки случая, когда ему необходимо вставить узел в корень дерева: [3]
void insert ( Node ** root , int key , int value ) { Node ** walk = root ; в то время как ( * прогулка ) { int curkey = ( * прогулка ) -> ключ ; if ( curkey == key ) { ( * прогулка ) -> значение = значение ; возврат ; } если ( клавиша > курсор ) прогулка = & ( * прогулка ) -> вправо ; иначе прогулка = & ( * прогулка ) -> влево ; } * прогулка = новый узел ( ключ , значение ); }Вышеупомянутый деструктивный процедурный вариант модифицирует дерево на месте. Он использует только постоянное пространство кучи (и итеративная версия также использует постоянное пространство стека), но предыдущая версия дерева теряется. В качестве альтернативы, как в следующем примере Python , мы можем восстановить всех предков вставленного узла; любая ссылка на исходный корень дерева остается действительной, делая дерево устойчивой структурой данных :
def binary_tree_insert ( node , key , value ): if node == None : вернуть NodeTree ( None , key , value , None ), если key == node . ключ : вернуть NodeTree ( узел . слева , ключ , значение , узел . справа ), если ключ < узел . ключ: return NodeTree ( binary_tree_insert ( узел . слева , ключ , значение ), node . key , node . value , node . right ) return NodeTree ( node . left , node . key , node . value , binary_tree_insert ( node . right , key , значение ))Перестраиваемая часть использует пространство O (log n ) в среднем случае и O ( n ) в худшем случае.
В любой версии для этой операции требуется время, пропорциональное высоте дерева в худшем случае, которое составляет O (log n ) времени в среднем по всем деревьям, но время O ( n ) в худшем случае.
Другой способ объяснить вставку состоит в том, что для вставки нового узла в дерево его ключ сначала сравнивается с ключом корня. Если его ключ меньше, чем у корня, он затем сравнивается с ключом левого потомка корня. Если его ключ больше, он сравнивается с правым дочерним элементом корня. Этот процесс продолжается до тех пор, пока новый узел не сравнивается с листовым узлом, а затем он добавляется как правый или левый дочерний узел этого узла, в зависимости от его ключа: если ключ меньше, чем ключ листа, то он вставляется как лист левый дочерний элемент, иначе как правый дочерний элемент листа.
Есть и другие способы вставки узлов в двоичное дерево, но это единственный способ вставки узлов в листья и в то же время с сохранением структуры BST.
Удаление [ править ]
При удалении узла из двоичного дерева поиска обязательно поддерживать упорядоченную последовательность узлов. Для этого есть много возможностей. Однако следующий метод, который был предложен Т. Хиббардом в 1962 году [4], гарантирует, что высота поддеревьев субъектов изменяется не более чем на единицу. Можно рассмотреть три возможных случая:
- Удаление узла без дочерних узлов: просто удалите узел из дерева.
- Удаление узла с одним дочерним элементом: удалите узел и замените его дочерним.
- Удаление узла D с двумя детьми: выбрать либо D «S в порядке- предшественника , или в порядке-преемник Е (смотри рисунок). Вместо удаления D , перезаписать его ключ и значение с E «с. [Примечание 2] Если E не имеет ребенка, удалить Е из предыдущего родителя G . Если у E есть дочерний элемент F , это правильный дочерний элемент, так что он должен заменить E в родительском элементе E.
Во всех случаях, когда D является корневым, снова сделайте замену корневого узла.
Узлы с двумя дочерними элементами удалить сложнее. Порядковый преемник узла - это самый левый дочерний элемент правого поддерева, а упорядоченный предшественник - самый правый дочерний элемент левого поддерева. В любом случае у этого узла будет только один дочерний элемент или вообще не будет. Удалите его в соответствии с одним из двух более простых случаев, описанных выше.
Последовательное использование упорядоченного преемника или упорядоченного предшественника для каждого экземпляра случая с двумя дочерними элементами может привести к несбалансированному дереву, поэтому некоторые реализации выбирают одно или другое в разное время.
Анализ во время выполнения: хотя эта операция не всегда перемещает дерево вниз до листа, это всегда возможно; таким образом, в худшем случае требуется время, пропорциональное высоте дерева. Он не требует большего, даже если у узла есть два дочерних узла, поскольку он по-прежнему следует по единственному пути и не посещает ни один узел дважды.
def find_min ( self ): "" "Получить минимальный узел в поддереве." "" current_node = self, а current_node . left_child : current_node = текущий_узел . left_child вернуть current_nodedef replace_node_in_parent ( self , new_value = None ) -> None : если self . родитель : если self == self . родитель . left_child : я . родитель . left_child = new_value еще : самостоятельно . родитель . right_child = new_value если new_value : new_value . родитель = я. родительdef binary_tree_delete ( self , key ) -> None : если ключ < self . ключ : я . left_child . binary_tree_delete ( ключ ) вернет, если ключ > self . ключ : я . right_child . binary_tree_delete ( key ) return # Удалите ключ здесь, если self . left_child и себя .right_child : # Если оба ребенка присутствуют, преемник = сам . right_child . find_min () самостоятельно . ключ = преемник . ключевой преемник . binary_tree_delete ( преемник . ключ ) elif self . left_child : # Если у узла есть только * left * дочерний элемент self . replace_node_in_parent ( self . left_child ) elif сам . right_child : # Если у узла есть только * правильное * дочернее я . replace_node_in_parent ( self . right_child ) else : self . replace_node_in_parent ( None ) # У этого узла нет потомковОбход [ править ]
После создания бинарного дерева поиска его элементы могут быть извлечены по порядку путем рекурсивного обхода левого поддерева корневого узла, доступа к самому узлу, а затем рекурсивного обхода правого поддерева узла, продолжая этот шаблон с каждым узлом в дерево при рекурсивном доступе. Как и в случае со всеми бинарными деревьями, можно провести обход перед предварительным порядком или обход после порядка , но ни то, ни другое вряд ли будет полезно для деревьев двоичного поиска . Обход двоичного дерева поиска по порядку всегда приводит к отсортированному списку узловых элементов (чисел, строк или других сопоставимых элементов).
Код для обхода по порядку в Python приведен ниже. Он будет вызывать обратный вызов (некоторая функция, которую программист хочет вызвать для значения узла, например, печать на экране) для каждого узла в дереве.
def traverse_binary_tree ( node , callback ): if node == None : return traverse_binary_tree ( node . leftChild , callback ) callback ( node . value ) traverse_binary_tree ( node . rightChild , callback )Для обхода требуется время O ( n ) , поскольку он должен посетить каждый узел. Этот алгоритм также O ( n ) , поэтому он асимптотически оптимален .
Обход также может быть реализован итеративно . Для некоторых приложений, например, поиска большего равенства, приближенного поиска, операции дляодношаговый (итеративный) обход может быть очень полезным. Это, конечно, реализовано без конструкции обратного вызова и требует O (1) в среднем и O (log n ) в худшем случае.
Подтверждение [ править ]
Иногда у нас уже есть двоичное дерево, и нам нужно определить, является ли оно BST. У этой проблемы есть простое рекурсивное решение.
Свойство BST - каждый узел в правом поддереве должен быть больше текущего узла, а каждый узел в левом поддереве должен быть меньше текущего узла - является ключом к выяснению того, является ли дерево BST или нет. Жадный алгоритм -Просто обхода дерева, на каждом узле проверки содержит ли узел значение больше , чем значение в левом ребенка и меньше , чем значение на правом ребенка не работает для всех случаев. Рассмотрим следующее дерево:
20 / \ 10 30 / \ 5 40
В приведенном выше дереве каждый узел удовлетворяет условию, что узел содержит значение больше, чем его левый дочерний элемент, и меньшее, чем его правый дочерний элемент, и все же это не BST: значение 5 находится в правом поддереве узла, содержащего 20 , нарушение собственности BST.
Вместо того, чтобы принимать решение, основанное исключительно на значениях узла и его дочерних узлов, нам также нужна информация, исходящая от родителя. В случае с деревом выше, если бы мы могли вспомнить об узле, содержащем значение 20, мы бы увидели, что узел со значением 5 нарушает контракт свойств BST.
Итак, условие, которое нам нужно проверить на каждом узле:
- если узел является левым потомком своего родителя, то он должен быть меньше (или равен) родительскому, и он должен передавать значение от своего родителя к правому поддереву, чтобы убедиться, что ни один из узлов в этом поддереве не больше чем родитель
- если узел является правым дочерним элементом своего родителя, тогда он должен быть больше, чем родительский, и он должен передать значение от своего родителя к своему левому поддереву, чтобы убедиться, что ни один из узлов в этом поддереве не меньше, чем родительский.
Рекурсивное решение на C ++ может объяснить это дальше:
struct TreeNode { int key ; значение int ; struct TreeNode * left ; struct TreeNode * right ; }; bool isBST ( struct TreeNode * node , int minKey , int maxKey ) { if ( node == NULL ) return true ; if ( node -> key < minKey || node -> key > maxKey ) return false ; return isBST ( node -> left , minKey , node -> key -1 ) && isBST ( node -> right , node -> key + 1 , maxKey ); }node->key+1и node->key-1сделаны, чтобы разрешить только отдельные элементы в BST.
Если мы хотим, чтобы одни и те же элементы присутствовали, то мы можем использовать только node->keyв обоих местах.
Первоначальный вызов этой функции может быть примерно таким:
если ( isBST ( корень , INT_MIN , INT_MAX )) { пут ( "Это БСТ." ); } else { put ( "Это НЕ BST!" ); }По сути, мы продолжаем создавать допустимый диапазон (начиная с [MIN_VALUE, MAX_VALUE]) и продолжаем сжимать его для каждого узла по мере рекурсивного спуска вниз.
Как указано в разделе #Traversal , обход двоичного дерева поиска по порядку возвращает отсортированные узлы. Таким образом, нам нужно только сохранить последний посещенный узел при обходе дерева и проверить, меньше ли его ключ (или меньше / равен, если в дереве допускаются дубликаты) по сравнению с текущим ключом.
Параллельные алгоритмы [ править ]
Существуют также параллельные алгоритмы для двоичных деревьев поиска, включая вставку / удаление нескольких элементов, построение из массива, фильтрацию с определенным предиктором, сглаживание в массив, слияние / вычитание / пересечение двух деревьев и т. Д. Эти алгоритмы могут быть реализованы с использованием основанных на объединении древовидные алгоритмы , которые также могут поддерживать балансировку дерева с использованием нескольких схем балансировки (включая дерево AVL , красно-черное дерево , дерево со сбалансированным весом и treap ).
Примеры приложений [ править ]
Сортировать [ редактировать ]
Бинарное дерево поиска можно использовать для реализации простого алгоритма сортировки . Подобно heapsort , мы вставляем все значения, которые хотим отсортировать, в новую упорядоченную структуру данных - в данном случае двоичное дерево поиска - и затем просматриваем ее по порядку.
Наихудшее время build_binary_tree- O ( n 2 ) - если вы скармливаете ему отсортированный список значений, он объединяет их в связанный список без левых поддеревьев. Например, build_binary_tree([1, 2, 3, 4, 5])дает дерево (1 (2 (3 (4 (5))))).
Существует несколько схем преодоления этого недостатка с помощью простых бинарных деревьев; наиболее распространенным является самобалансирующееся двоичное дерево поиска . Если эта же процедура выполняется с использованием такого дерева, общее время наихудшего случая составляет O ( n log n ) , что является асимптотически оптимальным для сортировки сравнения . На практике дополнительные накладные расходы во времени и пространстве для сортировки на основе дерева (особенно для распределения узлов ) делают ее менее эффективной по сравнению с другими асимптотически оптимальными сортировками, такими как heapsort для сортировки статических списков. С другой стороны, это один из самых эффективных методов инкрементальной сортировки., добавляя элементы в список с течением времени, сохраняя при этом список всегда отсортированным.
Операции с приоритетной очередью [ править ]
Деревья двоичного поиска могут служить очередями с приоритетом : структурами, которые позволяют вставлять произвольный ключ, а также выполнять поиск и удаление минимального (или максимального) ключа. Вставка работает, как объяснялось ранее. Find-min обходит дерево, следуя указателям слева, насколько это возможно, не касаясь листа:
// Предварительное условие : T не является листовой функцией find-min (T): while hasLeft (T): Т? слева (T) ключ возврата (T)
Find-max аналогичен: следуйте правым указателям насколько возможно. Delete-min ( max ) может просто найти минимум (максимум), а затем удалить его. Таким образом, и вставка, и удаление занимают логарифмическое время, как и в двоичной куче , но в отличие от двоичной кучи и большинства других реализаций приоритетной очереди, одно дерево может поддерживать все функции find-min , find-max , delete-min. и delete-max одновременно, что делает деревья двоичного поиска подходящими в качестве двусторонних очередей приоритетов . [2] : 156
Типы [ править ]
Существует много типов деревьев двоичного поиска. Деревья AVL и красно-черные деревья являются формами самобалансирующихся двоичных деревьев поиска . Расставленное дерево представляет собой бинарное дерево поиска , которое автоматически перемещает часто используемые элементы ближе к корню. В treap ( куче дерева ) каждый узел также имеет (случайно выбранный) приоритет, а родительский узел имеет более высокий приоритет, чем его дочерние элементы. Деревья танго - это деревья, оптимизированные для быстрого поиска. T-деревья - это бинарные деревья поиска, оптимизированные для уменьшения накладных расходов на дисковое пространство, широко используемые для баз данных в памяти.
Вырожденное дерево - это дерево, в котором для каждого родительского узла есть только один связанный дочерний узел. Он несбалансирован, и в худшем случае производительность снижается до уровня связанного списка. Если ваша функция добавления узла не обрабатывает повторную балансировку, вы можете легко построить вырожденное дерево, загрузив его данными, которые уже отсортированы. Это означает, что при измерении производительности дерево по существу ведет себя как структура данных связанного списка.
Сравнение производительности [ править ]
DA Heger (2004) [5] представил сравнение производительности деревьев двоичного поиска. Было обнаружено, что Treap имеет лучшую среднюю производительность, в то время как у красно-черного дерева наименьшее количество вариаций производительности.
Оптимальные бинарные деревья поиска [ править ]
Если дерево поиска не предназначено быть изменено, и это точно известно , как часто будет доступен каждый элемент, можно построить [6] оптимальное бинарное дерево поиска , который является деревом поиска , где средняя стоимость отрываясь элемент ( ожидаемая стоимость поиска ) сведен к минимуму.
Даже если у нас есть только оценки затрат на поиск, такая система может значительно ускорить поиск в среднем. Например, если у нас есть BST английских слов , используемых в орфографический , мы могли бы уравновесить дерево , основанное на частоте слов в текстовых корпусов , помещая слова , как возле корня и слова , как agerasia вблизи листьев. Такое дерево можно сравнить с деревьями Хаффмана , которые аналогичным образом стремятся разместить часто используемые элементы рядом с корнем, чтобы обеспечить плотное кодирование информации; однако деревья Хаффмана хранят элементы данных только в листьях, и эти элементы не нужно упорядочивать.
Если последовательность, в которой будет осуществляться доступ к элементам в дереве, заранее неизвестна, можно использовать расширяемые деревья , которые асимптотически не хуже любого статического дерева поиска, которое мы можем построить для любой конкретной последовательности операций поиска.
Алфавитные деревья - это деревья Хаффмана с дополнительным ограничением на порядок или, что то же самое, деревья поиска с модификацией, согласно которой все элементы хранятся в листьях. Существуют более быстрые алгоритмы для оптимальных алфавитно-двоичных деревьев (OABT).
См. Также [ править ]
- Алгоритм двоичного поиска
- Дерево поиска
- Самобалансирующееся двоичное дерево поиска
- AVL дерево
- Красно-черное дерево
- Рандомизированное двоичное дерево поиска
- Танго дерево
- Алгоритмы дерева на основе соединений
- Treap
- Балансированное дерево
Примечания [ править ]
- ^ Понятие среднего BST уточняется следующим образом. Пусть случайный BST построен с использованием только вставок из последовательности уникальных элементов в случайном порядке (все перестановки одинаково вероятны); тогда ожидаемая высота дерева равна O (log | Nodes |) . Если разрешены как удаления, так и вставки, «мало что известно о средней высоте двоичного дерева поиска». [1] : 300
- ^ Конечно, общий пакет программного обеспечения должен работать какнаоборот: он должен оставить пользовательские данные нетронутыми и отделку E со всей BST взаимосвязанных с D .
Ссылки [ править ]
- ^ а б Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стейн, Клиффорд (2009) [1990]. Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN 0-262-03384-4.
- ^ a b Мельхорн, Курт ; Сандерс, Питер (2008). Алгоритмы и структуры данных: The Basic Toolbox (PDF) . Springer.
- ^ Трубецкой, Григорий. «Линус по пониманию указателей» . Проверено 21 февраля 2019 .
- ^ Роберт Седжвик , Кевин Уэйн: четвертое издание алгоритмов. Pearson Education, 2011, ISBN 978-0-321-57351-3 , стр. 410.
- ^ Хегер, Доминик А. (2004), «Исследование характеристик производительности структур данных двоичного дерева поиска» (PDF) , European Journal for the Informatics Professional , 5 (5): 67–75, заархивировано из оригинала (PDF ) 27 марта 2014 г. , дата обращения 16.10.2010.
- ^ Гонне, Гастон. «Оптимальные бинарные деревья поиска» . Научные вычисления . ETH Zürich. Архивировано из оригинального 12 октября 2014 года . Проверено 1 декабря 2013 года .
Дальнейшее чтение [ править ]
 Эта статья включает материалы, являющиеся общественным достоянием из документа NIST : Блэк, Пол Э. «Дерево двоичного поиска» . Словарь алгоритмов и структур данных .
Эта статья включает материалы, являющиеся общественным достоянием из документа NIST : Блэк, Пол Э. «Дерево двоичного поиска» . Словарь алгоритмов и структур данных .- Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стейн, Клиффорд (2001). «12: деревья двоичного поиска, 15.5: оптимальные деревья двоичного поиска». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. С. 253–272, 356–363. ISBN 0-262-03293-7.
- Ярк, Дуэйн Дж. (3 декабря 2005 г.). «Обходы двоичного дерева» . Интерактивные визуализации структуры данных . Университет Мэриленда .
- Кнут, Дональд (1997). «6.2.2: Поиск в двоичном дереве». Искусство программирования . 3: «Сортировка и поиск» (3-е изд.). Эддисон-Уэсли. С. 426–458. ISBN 0-201-89685-0.
- Долго, Шон. «Дерево двоичного поиска» ( PPT ) . Визуализация структур данных и алгоритмов - подход на основе слайдов PowerPoint . СУНИ Онеонта .
- Парланте, Ник (2001). «Бинарные деревья» . Образовательная библиотека CS . Стэнфордский университет .
Внешние ссылки [ править ]
- Визуализатор двоичного дерева (JavaScript-анимация различных структур данных на основе BT)
- Мадру, Джастин (18 августа 2009 г.). «Дерево двоичного поиска» . JDServer . Архивировано из оригинального 28 марта 2010 года. Реализация на C ++.
- Пример двоичного дерева поиска в Python
- «Ссылки на указатели (C ++)» . MSDN . Microsoft . 2005 г. Дает пример реализации двоичного дерева.