| Звезда | |
|---|---|
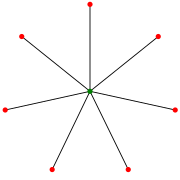 Звезда S 7 . (Некоторые авторы индексируют это как S 8. ) | |
| Вершины | к + 1 |
| Края | k |
| Диаметр | минимум (2, k ) |
| Обхват | ∞ |
| Хроматическое число | минимум (2, k + 1) |
| Хроматический индекс | k |
| Характеристики | Краевое транзитивное дерево Единичное расстояние Двудольное |
| Обозначение | S k |
| Таблица графиков и параметров | |
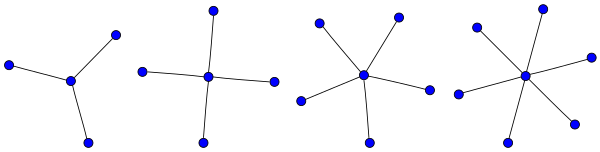
В теории графов , А звезда S к является полный двудольный граф K 1, K : а дерево с одним внутренним узлом и K листьев (но без внутренних узлов и K + 1 листьев , когда к ≤ 1). В качестве альтернативы некоторые авторы определяют S k как дерево порядка k с максимальным диаметром 2; в этом случае звезда с k > 2 имеет k - 1 лист.
Звезда с 3-мя гранями называется клешней .
Звезда S к является краевой изящным , когда к четно и не тогда , когда к нечетно. Это реберно-транзитивный граф спичечный , и имеет диаметр 2 (когда k > 1), обхват ∞ (у него нет циклов), хроматический индекс k и хроматическое число 2 (когда k > 0). Кроме того, звезда имеет большую группу автоморфизмов, а именно симметрическую группу из k букв.
Звезды также можно описать как единственные связные графы, в которых не более одной вершины имеет степень больше единицы.
Связь с другими семействами графов [ править ]
Когти примечательны в определении графов без клешней, графов , которые не имеют клешней в качестве индуцированного подграфа . [1] [2] Они также являются одним из исключительных случаев теоремы об изоморфизме графов Уитни : в общем случае графы с изоморфными линейными графами сами изоморфны, за исключением клешни и треугольника K 3 . [3]
Звезда - это особый вид дерева . Как и в случае с любым деревом, звезды могут быть закодированы последовательностью Прюфера ; последовательность Прюфера для звезды K 1, k состоит из k - 1 копии центральной вершины. [4]
Несколько инвариантов графов определены в терминах звезд. Звездная древовидность - это минимальное количество лесов, на которые граф можно разбить так, чтобы каждое дерево в каждом лесу было звездой [5], а звездное хроматическое число графа - это минимальное количество цветов, необходимых для окраски его вершин в такие способ, которым каждые два цветовых класса вместе образуют подграф, в котором все связанные компоненты являются звездами. [6] Графики ширины ветвления 1 - это в точности графы, в которых каждый компонент связности является звездой. [7]
Другие приложения [ править ]
Набор расстояний между вершинами когтя представляет собой пример конечного метрического пространства, которое не может быть изометрически вложено в евклидово пространство любой размерности. [8]
Звездой сети , А компьютерная сеть по образцу звезды графика, играет важную роль в распределенных вычислений .
Геометрическая реализация звездного графа, образованная путем отождествления ребер с интервалами некоторой фиксированной длины, используется в качестве локальной модели кривых в тропической геометрии . Тропическая кривая определяется как метрическое пространство, локально изоморфное звездному метрическому графу.
Ссылки [ править ]
| Викискладе есть медиафайлы, связанные со звездными графами . |
- ^ Фодри, Ральф ; Фландрин, Эвелин; Ryjáček, Зденек (1997), "лапка свободной графики - опрос А", дискретной математики , 164 (1-3): 87-147, DOI : 10.1016 / S0012-365X (96) 00045-3 , МР 1432221.
- ↑ Чудновский, Мария ; Сеймур, Пол (2005), "Структура графов без клешней", Обзоры по комбинаторике 2005 (PDF) , London Math. Soc. Lecture Note Ser., 327 , Cambridge: Cambridge Univ. Press, стр. 153–171, MR 2187738 .
- ^ Уитня, Hassler (январь 1932), "Конгруэнтные Графы и Связность графов", Американский журнал математика , 54 (1): 150-168, DOI : 10,2307 / 2371086 , ЛВП : 10338.dmlcz / 101067 , JSTOR 2371086 .
- ^ Gottlieb, J .; Julstrom, BA; Rothlauf, F .; Райдл, GR (2001). «Числа Прюфера: плохое представление остовных деревьев для эволюционного поиска» (PDF) . GECCO-2001: Труды конференции по генетическим и эволюционным вычислениям . Морган Кауфманн. С. 343–350. ISBN 1558607749.
- ^ Хакими, SL; Mitchem, J .; Шмейхель, EE (1996), "Звездная древовидность графов", Discrete Math. , 149 : 93–98, DOI : 10.1016 / 0012-365X (94) 00313-8
- ^ Фертин, Гийом; Распо, Андре; Рид, Брюс (2004), "Звезда раскраски графов" , Журнал теории графов , 47 (3): 163-182, DOI : 10.1002 / jgt.20029.
- ^ Робертсон, Нил ; Сеймура, Пол Д. (1991), "Graph несовершеннолетнего X. Препятствие к разложению дерева.", Журнал комбинаторной теории , 52 (2): 153-190, DOI : 10.1016 / 0095-8956 (91) 90061-N.
- ^ Linial, Натан (2002), "Конечные метрические пространства – комбинаторика, геометрия и алгоритмы", Proc. Международный конгресс математиков, Пекин , 3 , стр. 573–586, arXiv : math / 0304466 , Bibcode : 2003math ...... 4466L