Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску

В теории вычислений и теории автоматов , то конструкция Powerset или строительство подмножества является стандартным методом для преобразования в недетерминированный конечный автомате (НКА) в детерминированный конечный автомат (DFA) , который распознает один и тот же формальный язык . Это важно в теории, поскольку устанавливает, что NFA, несмотря на их дополнительную гибкость, не могут распознавать любой язык, который не может быть распознан некоторыми DFA. Это также важно на практике для преобразования простых в создании NFA в более эффективно исполняемые DFA. Однако, если в NFA есть nсостояний, результирующий DFA может иметь до 2 n состояний, экспоненциально большее число, что иногда делает конструкцию непрактичной для больших NFA.

Конструкция, которую иногда называют конструкцией степенного набора Рабина – Скотта (или конструкцией подмножества), чтобы отличить ее от аналогичных конструкций для других типов автоматов, была впервые опубликована Майклом О. Рабином и Даной Скотт в 1959 г. [1]

Интуиция [ править ]

Чтобы смоделировать работу DFA с заданной входной строкой, необходимо отслеживать одно состояние в любое время: состояние, которого автомат достигнет после просмотра префикса входных данных. Напротив, для моделирования NFA необходимо отслеживать набор состояний: все состояния, которые автомат может достичь после просмотра одного и того же префикса ввода, в соответствии с недетерминированным выбором, сделанным автоматом. Если после определенного префикса входа может быть достигнут набор состояний S , то после следующего символа входа x набор достижимых состояний является детерминированной функцией S и x. Следовательно, наборы достижимых состояний NFA играют в моделировании NFA ту же роль, что и отдельные состояния DFA в моделировании DFA, и на самом деле наборы состояний NFA, появляющиеся в этой симуляции, могут быть повторно интерпретированы как состояния DFA. [2]

Строительство [ править ]

Конструкция powerset наиболее непосредственно применима к NFA, которая не допускает преобразования состояний без использования входных символов (также известных как «ε-перемещения»). Такой автомат можно определить как набор из 5 ( Q , Σ, T , q 0 , F ) , в котором Q - это набор состояний, Σ - набор входных символов, T - функция перехода (отображение состояния и входной символ для набора состояний), q 0 - начальное состояние, а F - набор принимающих состояний. Соответствующий ДКА имеет состояния, соответствующие подмножествам Q. Начальное состояние DFA - это { q 0 } , (одноэлементный) набор начальных состояний. Функция перехода DFA отображает состояние S (представляющее подмножество Q ) и входной символ x на множество T ( S , x ) = ∪ { T ( q , x ) | д ∈ S } , множество всех состояний , которые могут быть достигнуты с помощью й -перехода из состояния в S . Состояние S DFA является принимающим состоянием тогда и только тогда, когда хотя бы один член Sявляется принимающим государством NFA. [2] [3]

В простейшем варианте конструкции POWERSET, множество всех состояний ДКА является Powerset из Q , множество всех возможных подмножеств Q . Однако многие состояния результирующего DFA могут оказаться бесполезными, поскольку они могут быть недоступны из исходного состояния. Альтернативный вариант конструкции создает только реально достижимые состояния. [4]

NFA с ε-ходами [ править ]

Для НКА с е-ходов (также называется ε-НКА), конструкция должна быть изменена , чтобы иметь дело с этими вычисляя Е- замыкание состояний: множество всех состояний , достижимых из некоторого заданного состояния , используя только е-ходы. Ван Норд выделяет три возможных способа включения этого вычисления замыкания в конструкцию powerset: [5]

  1. Вычислите ε-замыкание всего автомата как шаг предварительной обработки, создав эквивалентный NFA без ε-ходов, затем примените обычную конструкцию powerset. Эта версия, также обсуждаемая Хопкрофтом и Уллманом [6] , проста в реализации, но непрактична для автоматов с большим количеством ε-ходов, которые обычно возникают в приложениях обработки естественного языка . [5]
  2. Во время вычисления набора мощности вычислите ε-замыкание каждого состояния q , которое учитывается алгоритмом (и кешируйте результат).
  3. Во время вычисления набора мощности вычислите ε-замыкание каждого подмножества состояний Q ' , которое учитывается алгоритмом, и добавьте его элементы к Q' .

Несколько начальных состояний [ править ]

Если NFA определены с учетом нескольких начальных состояний, [7] начальное состояние соответствующего DFA - это набор всех начальных состояний NFA или (если NFA также имеет ε-ходы) набор всех состояний, достижимых из начальные состояния ε-ходами.

Пример [ править ]

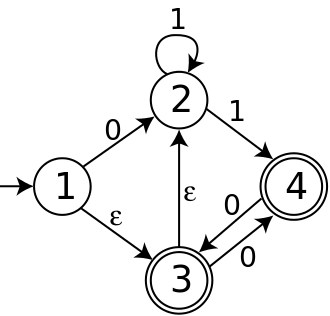
NFA, представленная ниже, имеет четыре состояния; состояние 1 является начальным, а состояния 3 и 4 - допустимыми. Его алфавит состоит из двух символов 0 и 1 и имеет ε-ходы.

NFA-powerset-construction-example.svg

Начальное состояние DFA, построенного из этой NFA, является набором всех состояний NFA, которые достижимы из состояния 1 с помощью ε-ходов; то есть это набор {1,2,3}. Переход от {1,2,3} входным символом 0 должен следовать либо по стрелке из состояния 1 в состояние 2, либо по стрелке из состояния 3 в состояние 4. Кроме того, ни состояние 2, ни состояние 4 не имеют исходящих ε-перемещений. Следовательно, T ({1,2,3}, 0) = {2,4}, и по тем же соображениям полный DFA, построенный из NFA, показан ниже.

DFA-powerset-construction-example.svg

Как видно из этого примера, есть пять состояний, достижимых из начального состояния DFA; остальные 11 наборов в powerset набора состояний NFA недостижимы.

Сложность [ править ]

Основная статья: Государственная сложность
NFA с 5 состояниями (слева), для DFA (справа) требуется 16 состояний. [4]

Поскольку состояния DFA состоят из наборов состояний NFA, NFA с n- состояниями может быть преобразован в DFA с не более чем 2 n состояниями. [2] Для каждого n существует n -состояний NFA, такое что каждое подмножество состояний достижимо из начального подмножества, так что преобразованный DFA имеет ровно 2 n состояний, что дает ( 2 n ) наихудшую временную сложность. [8] [9] Простым примером, требующим почти такого количества состояний, является язык строк в алфавите {0,1}, в котором не менее n символов, nth из последнего из которых равен 1. Он может быть представлен NFA с ( n + 1) -состоянием, но для этого требуется 2 n состояний DFA, по одному для каждого суффикса n- символа ввода; ср. картинка для n = 4 . [4]

Приложения [ править ]

Алгоритм Бжозовского для минимизации DFA использует конструкцию powerset дважды. Он преобразует входной DFA в NFA для обратного языка, переворачивая все его стрелки и меняя роли начального и принимающего состояний, преобразует NFA обратно в DFA, используя конструкцию powerset, а затем повторяет свой процесс. Его сложность наихудшего случая является экспоненциальной, в отличие от некоторых других известных алгоритмов минимизации DFA, но во многих примерах он работает быстрее, чем можно было бы предположить по сложности наихудшего случая. [10]

Конструкция Сафры , которая преобразует недетерминированный автомат Бюхи с n состояниями в детерминированный автомат Мюллера или в детерминированный автомат Рабина с 2 O ( n log n ) состояниями, использует конструкцию powerset как часть своего механизма. [11]

Ссылки [ править ]

  1. ^ Рабин, Миссури ; Скотт, Д. (1959). «Конечные автоматы и проблемы их решения». Журнал исследований и разработок IBM . 3 (2): 114–125. DOI : 10.1147 / rd.32.0114 . ISSN  0018-8646 .
  2. ^ a b c Сипсер, Майкл . «Теорема 1.19». Введение в теорию вычислений . С.  55–56 . ISBN 0-534-94728-X.
  3. ^ Хопкрофт, Джон Э .; Ульман, Джеффри Д. (1979). «Эквивалентность DFA и NFA». Введение в теорию автоматов, языки и вычисления . Чтение Массачусетса: Эддисон-Уэсли. С.  22–23 . ISBN 0-201-02988-X.CS1 maint: ref = harv ( ссылка )
  4. ^ a b c Шнайдер, Клаус (2004). Верификация реактивных систем: формальные методы и алгоритмы . Springer. С. 210–212. ISBN 978-3-540-00296-3.
  5. ^ a b Ван Норд, Гертьян (2000). «Обработка эпсилон-движений в построении подмножеств» . Компьютерная лингвистика . 26 (1): 61–76. arXiv : cmp-lg / 9804003 . DOI : 10.1162 / 089120100561638 .
  6. ↑ Hopcroft & Ullman (1979) , стр. 26–27.
  7. ^ Рота, Йорг (2006). Теория сложности и криптология: введение в криптосложность . Тексты по теоретической информатике. Springer. С. 21–22. ISBN 9783540285205..
  8. ^ Лупанов Олег Б. (1963). «Сравнение двух типов конечных источников». Проблемы Кибернетики . 9 : 321–326.
  9. ^ Мур, Фрэнк Р. (1971). «О границах размера множества состояний в доказательствах эквивалентности детерминированных, недетерминированных и двусторонних конечных автоматов». Транзакции IEEE на компьютерах . С-20 (10): 1211–1214. DOI : 10.1109 / TC.1971.223108 ..
  10. Перейти ↑ Brzozowski, JA (1963). «Канонические регулярные выражения и минимальные графы состояний для определенных событий». Proc. Симпозиумы. Математика. Теория автоматов (Нью-Йорк, 1962) . Политехническая пресса Политехнического института. of Brooklyn, Brooklyn, NY, стр. 529–561. Руководство по ремонту 0175719 . 
  11. ^ Сафра, С. (1988). «О сложности ω-автоматов». Материалы 29-го ежегодного симпозиума по основам информатики (FOCS '88) . Вашингтон, округ Колумбия, США: Компьютерное общество IEEE. С. 319–327. DOI : 10.1109 / SFCS.1988.21948 ..

Дальнейшее чтение [ править ]

  • Андерсон, Джеймс Эндрю (2006). Теория автоматов в современных приложениях . Издательство Кембриджского университета. С. 43–49. ISBN 978-0-521-84887-9.