Метод сопряженных градиентов

Сравнение сходимости градиентного спуска с оптимальным размером шага (зеленым) и сопряженным вектором (красным) для минимизации квадратичной функции, связанной с данной линейной системой. Сопряженный градиент, предполагающий точную арифметику, сходится не более чем за n шагов, где n - размер матрицы системы (здесь n  = 2).

In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.

Метод сопряженных градиентов также может использоваться для решения задач неограниченной оптимизации, таких как минимизация энергии . Его обычно приписывают Магнусу Хестенсу и Эдуарду Штифелю , ^{[1] [2],} которые программировали его на Z4 , ^[3] и тщательно исследовали. ^{[4] [5]}

Метод двусопряженных градиентов обеспечивает обобщение на несимметричные матрицы. Различные нелинейные методы сопряженных градиентов ищут минимум нелинейных уравнений и целевых функций черного ящика.

Описание проблемы, решаемой сопряженными градиентами [ править ]

Предположим, мы хотим решить систему линейных уравнений

${\displaystyle \mathbf {A} \mathbf {x} =\mathbf {b} }$

для вектора , где известная матрица является симметричной (т. е. A ^T = A ), положительно определенной (т. е. x ^T Ax > 0 для всех ненулевых векторов в R ⁿ ) и действительной , и также известна. Обозначим единственное решение этой системы через .${\displaystyle \mathbf {x} }$${\displaystyle n\times n}$${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {x} }$${\displaystyle \mathbf {b} }$${\displaystyle \mathbf {x} _{*}}$

Деривация как прямой метод [ править ]

The conjugate gradient method can be derived from several different perspectives, including specialization of the conjugate direction method for optimization, and variation of the Arnoldi/Lanczos iteration for eigenvalue problems. Despite differences in their approaches, these derivations share a common topic—proving the orthogonality of the residuals and conjugacy of the search directions. These two properties are crucial to developing the well-known succinct formulation of the method.

We say that two non-zero vectors u and v are conjugate (with respect to ${\displaystyle \mathbf {A} }$) if

${\displaystyle \mathbf {u} ^{\mathsf {T}}\mathbf {A} \mathbf {v} =0.}$

Since ${\displaystyle \mathbf {A} }$ is symmetric and positive-definite, the left-hand side defines an inner product

${\displaystyle \mathbf {u} ^{\mathsf {T}}\mathbf {A} \mathbf {v} =\langle \mathbf {u} ,\mathbf {v} \rangle _{\mathbf {A} }:=\langle \mathbf {A} \mathbf {u} ,\mathbf {v} \rangle =\langle \mathbf {u} ,\mathbf {A} ^{\mathsf {T}}\mathbf {v} \rangle =\langle \mathbf {u} ,\mathbf {A} \mathbf {v} \rangle .}$

Два вектора сопряжены тогда и только тогда, когда они ортогональны по отношению к этому внутреннему произведению. Сопряжение - это симметричное отношение: если сопряжено с , то сопряжено с . Предположим, что${\displaystyle \mathbf {u} }$${\displaystyle \mathbf {v} }$${\displaystyle \mathbf {v} }$${\displaystyle \mathbf {u} }$

${\displaystyle P=\{\mathbf {p} _{1},\dots ,\mathbf {p} _{n}\}}$

представляет собой набор взаимно сопряженных векторов относительно , т . Тогда образует основу для , и мы можем выразить решение о в этом базисе:${\displaystyle n}$${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {p} _{i}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{j}=\delta _{ij}}$${\displaystyle P}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbf {x} _{*}}$${\displaystyle \mathbf {Ax} =\mathbf {b} }$

${\displaystyle \mathbf {x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {p} _{i}\Rightarrow \mathbf {A} \mathbf {x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {A} \mathbf {p} _{i}.}$

Умножение слева на урожайность${\displaystyle \mathbf {p} _{k}^{\mathsf {T}}}$

${\displaystyle \mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {x} _{*}=\sum _{i=1}^{n}\alpha _{i}\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{i}\Rightarrow \mathbf {p} _{k}^{\mathsf {T}}\mathbf {b} =\sum _{i=1}^{n}\alpha _{i}\left\langle \mathbf {p} _{k},\mathbf {p} _{i}\right\rangle _{\mathbf {A} }=\alpha _{k}\left\langle \mathbf {p} _{k},\mathbf {p} _{k}\right\rangle _{\mathbf {A} }\Rightarrow }$

${\displaystyle \alpha _{k}={\frac {\langle \mathbf {p} _{k},\mathbf {b} \rangle }{\langle \mathbf {p} _{k},\mathbf {p} _{k}\rangle _{\mathbf {A} }}}.}$

Это дает следующий метод ^[4] для решения уравнения Ax = b : найти последовательность сопряженных направлений, а затем вычислить коэффициенты α _k .${\displaystyle n}$

Как итеративный метод [ править ]

Если мы тщательно выберем сопряженные векторы , тогда нам могут не понадобиться все они для получения хорошего приближения к решению . Итак, мы хотим рассматривать метод сопряженных градиентов как итерационный метод. Это также позволяет нам приближенно решать системы, в которых n настолько велико, что прямой метод потребует слишком много времени.${\displaystyle \mathbf {p} _{k}}$${\displaystyle \mathbf {x} _{*}}$

Обозначим начальное предположение для x _∗ через x ₀ (без ограничения общности можно считать, что x ₀ = 0 , иначе вместо этого рассмотрим систему Az = b - Ax ₀ ). Начиная с x _0, мы ищем решение, и на каждой итерации нам нужна метрика, чтобы сказать нам, ближе ли мы к решению x _∗ (которое нам неизвестно). Эта метрика возникает из того факта, что решение x _∗ также является единственным минимизатором следующей квадратичной функции

${\displaystyle f(\mathbf {x} )={\tfrac {1}{2}}\mathbf {x} ^{\mathsf {T}}\mathbf {A} \mathbf {x} -\mathbf {x} ^{\mathsf {T}}\mathbf {b} ,\qquad \mathbf {x} \in \mathbf {R} ^{n}\,.}$

Существование единственного минимизатора очевидно, поскольку его вторая производная задается симметричной положительно определенной матрицей

${\displaystyle \nabla ^{2}f(\mathbf {x} )=\mathbf {A} \,,}$

и что минимизатор (используйте D f ( x ) = 0) решает исходную задачу, очевидно из его первой производной

${\displaystyle \nabla f(\mathbf {x} )=\mathbf {A} \mathbf {x} -\mathbf {b} \,.}$

Это предлагает принять первый базисный вектор p ₀ как отрицательное значение градиента f при x = x ₀ . Градиент f равен Ax - b . Начиная с первоначального предположения x ₀ , это означает, что мы берем p ₀ = b - Ax ₀ . Другие векторы в базисе будут сопряжены с градиентом, отсюда и название метод сопряженного градиента . Обратите внимание, что p ₀ также является невязкой, обеспечиваемой этим начальным шагом алгоритма.

Пусть r _k - невязка на k- м шаге:

${\displaystyle \mathbf {r} _{k}=\mathbf {b} -\mathbf {Ax} _{k}.}$

Как отмечалось выше, это отрицательный градиент at , поэтому метод градиентного спуска потребует перемещения в направлении r _k . Однако здесь мы настаиваем на том, чтобы направления были сопряжены друг другу. Практический способ обеспечить это - требовать, чтобы следующее направление поиска строилось из текущего остатка и всех предыдущих направлений поиска. Ограничение сопряжения является ограничением ортонормированного типа, и поэтому алгоритм можно рассматривать как пример ортонормировки Грама-Шмидта . Это дает следующее выражение:${\displaystyle \mathbf {r} _{k}}$${\displaystyle f}$${\displaystyle \mathbf {x} _{k}}$${\displaystyle \mathbf {p} _{k}}$

${\displaystyle \mathbf {p} _{k}=\mathbf {r} _{k}-\sum _{i<k}{\frac {\mathbf {p} _{i}^{\mathsf {T}}\mathbf {A} \mathbf {r} _{k}}{\mathbf {p} _{i}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{i}}}\mathbf {p} _{i}}$

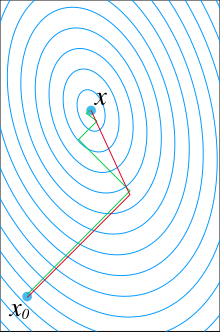
(см. изображение в верхней части статьи, чтобы увидеть влияние ограничения сопряженности на сходимость). Следуя этому направлению, следующее оптимальное местоположение задается

${\displaystyle \mathbf {x} _{k+1}=\mathbf {x} _{k}+\alpha _{k}\mathbf {p} _{k}}$

с участием

${\displaystyle \alpha _{k}={\frac {\mathbf {p} _{k}^{\mathsf {T}}(\mathbf {b} -\mathbf {Ax} _{k})}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}={\frac {\mathbf {p} _{k}^{\mathsf {T}}\mathbf {r} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}},}$

где последнее равенство следует из определения . Выражение для может быть получено, если подставить выражение для x _{k +1} в f и минимизировать его по${\displaystyle \mathbf {r} _{k}}$${\displaystyle \alpha _{k}}$${\displaystyle \alpha _{k}}$

${\displaystyle {\begin{aligned}f(\mathbf {x} _{k+1})&=f(\mathbf {x} _{k}+\alpha _{k}\mathbf {p} _{k})=:g(\alpha _{k})\\g'(\alpha _{k})&{\overset {!}{=}}0\quad \Rightarrow \quad \alpha _{k}={\frac {\mathbf {p} _{k}^{\mathsf {T}}(\mathbf {b} -\mathbf {Ax} _{k})}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}\,.\end{aligned}}}$

Результирующий алгоритм [ править ]

Вышеупомянутый алгоритм дает наиболее прямое объяснение метода сопряженных градиентов. По-видимому, заявленный алгоритм требует хранения всех предыдущих направлений поиска и векторов остатков, а также множества умножений матрицы на вектор и, следовательно, может быть дорогостоящим в вычислительном отношении. Однако более внимательный анализ алгоритма показывает, что он ортогонален , т. Е. Для i ≠ j. И является -ортогональным , т . Е. Для . Это можно рассматривать по мере продвижения алгоритма и охватывать одно и то же подпространство Крылова . Где формируют ортогональную основу по отношению к стандартному внутреннему продукту, и${\displaystyle \mathbf {r} _{i}}$${\displaystyle \mathbf {r} _{j}}$${\displaystyle \mathbf {r} _{i}^{\mathsf {T}}\mathbf {r} _{j}=0}$${\displaystyle \mathbf {p} _{i}}$${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {p} _{j}}$${\displaystyle \mathbf {p} _{i}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{j}=0}$${\displaystyle i\neq j}$${\displaystyle \mathbf {p} _{i}}$${\displaystyle \mathbf {r} _{i}}$${\displaystyle \mathbf {r} _{i}}$${\displaystyle \mathbf {p} _{i}}$образуют ортогональный базис по отношению к внутреннему произведению, индуцированному . Следовательно, можно рассматривать как проекцию на подпространство Крылова.${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {x} _{k}}$${\displaystyle \mathbf {x} }$

Ниже подробно описан алгоритм решения Ax = b, где - действительная, симметричная, положительно определенная матрица. Входной вектор может быть приближенным начальным решением или 0 . Это другая формулировка точной процедуры, описанной выше.${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {x} _{0}}$

${\displaystyle {\begin{aligned}&\mathbf {r} _{0}:=\mathbf {b} -\mathbf {Ax} _{0}\\&{\hbox{if }}\mathbf {r} _{0}{\text{ is sufficiently small, then return }}\mathbf {x} _{0}{\text{ as the result}}\\&\mathbf {p} _{0}:=\mathbf {r} _{0}\\&k:=0\\&{\text{repeat}}\\&\qquad \alpha _{k}:={\frac {\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {Ap} _{k}}}\\&\qquad \mathbf {x} _{k+1}:=\mathbf {x} _{k}+\alpha _{k}\mathbf {p} _{k}\\&\qquad \mathbf {r} _{k+1}:=\mathbf {r} _{k}-\alpha _{k}\mathbf {Ap} _{k}\\&\qquad {\hbox{if }}\mathbf {r} _{k+1}{\text{ is sufficiently small, then exit loop}}\\&\qquad \beta _{k}:={\frac {\mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {r} _{k+1}}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}}\\&\qquad \mathbf {p} _{k+1}:=\mathbf {r} _{k+1}+\beta _{k}\mathbf {p} _{k}\\&\qquad k:=k+1\\&{\text{end repeat}}\\&{\text{return }}\mathbf {x} _{k+1}{\text{ as the result}}\end{aligned}}}$

Это наиболее часто используемый алгоритм. Та же формула для β _k также используется в методе нелинейных сопряженных градиентов Флетчера – Ривза .

Перезапускается [ править ]

Отметим, что это вычисляется методом градиентного спуска, примененным к . Установка аналогичным образом могла бы сделать вычисление методом градиентного спуска от , т. Е. Может использоваться как простая реализация перезапуска итераций сопряженного градиента. ^[4] Перезапуски могут замедлить сходимость, но могут улучшить стабильность, если метод сопряженного градиента работает неправильно, например, из -за ошибки округления .${\displaystyle \mathbf {x} _{1}}$${\displaystyle \mathbf {x} _{0}}$${\displaystyle \beta _{k}=0}$${\displaystyle \mathbf {x} _{k+1}}$${\displaystyle \mathbf {x} _{k}}$

Явный расчет невязки [ править ]

Формулы и , которые имеют точную арифметику, делают формулы и математически эквивалентными. Первый используется в алгоритме, чтобы избежать дополнительного умножения на, поскольку вектор уже вычислен для оценки . Последнее может быть более точным, заменяя явное вычисление неявным вычислением рекурсией, подверженной накоплению ошибок округления , и поэтому рекомендуется для периодической оценки. ^[6]${\displaystyle \mathbf {x} _{k+1}:=\mathbf {x} _{k}+\alpha _{k}\mathbf {p} _{k}}$${\displaystyle \mathbf {r} _{k}:=\mathbf {b} -\mathbf {Ax} _{k}}$${\displaystyle \mathbf {r} _{k+1}:=\mathbf {r} _{k}-\alpha _{k}\mathbf {Ap} _{k}}$${\displaystyle \mathbf {r} _{k+1}:=\mathbf {b} -\mathbf {Ax} _{k+1}}$${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {Ap} _{k}}$${\displaystyle \alpha _{k}}$${\displaystyle \mathbf {r} _{k+1}:=\mathbf {b} -\mathbf {Ax} _{k+1}}$

Вычисление альфа и бета [ править ]

В алгоритме α _k выбирается таким, чтобы он был ортогонален r _k . Знаменатель упрощен из${\displaystyle \mathbf {r} _{k+1}}$

${\displaystyle \alpha _{k}={\frac {\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}={\frac {\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {Ap} _{k}}}}$

since ${\displaystyle \mathbf {r} _{k+1}=\mathbf {p} _{k+1}-\mathbf {\beta } _{k}\mathbf {p} _{k}}$. The β_k is chosen such that ${\displaystyle \mathbf {p} _{k+1}}$ is conjugated to p_k. Initially, β_k is

${\displaystyle \beta _{k}=-{\frac {\mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}}}}$

using

${\displaystyle \mathbf {r} _{k+1}=\mathbf {r} _{k}-\alpha _{k}\mathbf {A} \mathbf {p} _{k}}$

and equivalently

${\displaystyle \mathbf {A} \mathbf {p} _{k}={\frac {1}{\alpha _{k}}}(\mathbf {r} _{k}-\mathbf {r} _{k+1}),}$

the numerator of β_k is rewritten as

${\displaystyle \mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}={\frac {1}{\alpha _{k}}}\mathbf {r} _{k+1}^{\mathsf {T}}(\mathbf {r} _{k}-\mathbf {r} _{k+1})=-{\frac {1}{\alpha _{k}}}\mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {r} _{k+1}}$

because ${\displaystyle \mathbf {r} _{k+1}}$ and r_k are orthogonal by design. The denominator is rewritten as

${\displaystyle \mathbf {p} _{k}^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}=(\mathbf {r} _{k}+\beta _{k-1}\mathbf {p} _{k-1})^{\mathsf {T}}\mathbf {A} \mathbf {p} _{k}={\frac {1}{\alpha _{k}}}\mathbf {r} _{k}^{\mathsf {T}}(\mathbf {r} _{k}-\mathbf {r} _{k+1})={\frac {1}{\alpha _{k}}}\mathbf {r} _{k}^{\mathsf {T}}\mathbf {r} _{k}}$

using that the search directions p_k are conjugated and again that the residuals are orthogonal. This gives the β in the algorithm after cancelling α_k.

Example code in MATLAB / GNU Octave[edit]

функция  x = конград ( A, b, x )   г = Ь - А * х ;       р = г ;   rsold = r ' * r ;     для i = 1 : длина ( b )    Ap = A * p ;     альфа = rsold / ( p ' * Ap );       х = х + альфа * р ;       r = r - alpha * Ap; rsnew = r' * r; if sqrt(rsnew) < 1e-10 break end p = r + (rsnew / rsold) * p; rsold = rsnew; endend

Numerical example[edit]

Consider the linear system Ax = b given by

${\displaystyle \mathbf {A} \mathbf {x} ={\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}={\begin{bmatrix}1\\2\end{bmatrix}},}$

we will perform two steps of the conjugate gradient method beginning with the initial guess

${\displaystyle \mathbf {x} _{0}={\begin{bmatrix}2\\1\end{bmatrix}}}$

in order to find an approximate solution to the system.

Solution[edit]

For reference, the exact solution is

${\displaystyle \mathbf {x} ={\begin{bmatrix}{\frac {1}{11}}\\\\{\frac {7}{11}}\end{bmatrix}}\approx {\begin{bmatrix}0.0909\\\\0.6364\end{bmatrix}}}$

Our first step is to calculate the residual vector r₀ associated with x₀. This residual is computed from the formula r₀ = b - Ax₀, and in our case is equal to

${\displaystyle \mathbf {r} _{0}={\begin{bmatrix}1\\2\end{bmatrix}}-{\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix}2\\1\end{bmatrix}}={\begin{bmatrix}-8\\-3\end{bmatrix}}=\mathbf {p} _{0}.}$

Since this is the first iteration, we will use the residual vector r₀ as our initial search direction p₀; the method of selecting p_k will change in further iterations.

We now compute the scalar α₀ using the relationship

${\displaystyle \alpha _{0}={\frac {\mathbf {r} _{0}^{\mathsf {T}}\mathbf {r} _{0}}{\mathbf {p} _{0}^{\mathsf {T}}\mathbf {Ap} _{0}}}={\frac {{\begin{bmatrix}-8&-3\end{bmatrix}}{\begin{bmatrix}-8\\-3\end{bmatrix}}}{{\begin{bmatrix}-8&-3\end{bmatrix}}{\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix}-8\\-3\end{bmatrix}}}}={\frac {73}{331}}.}$

We can now compute x₁ using the formula

${\displaystyle \mathbf {x} _{1}=\mathbf {x} _{0}+\alpha _{0}\mathbf {p} _{0}={\begin{bmatrix}2\\1\end{bmatrix}}+{\frac {73}{331}}{\begin{bmatrix}-8\\-3\end{bmatrix}}={\begin{bmatrix}0.2356\\0.3384\end{bmatrix}}.}$

This result completes the first iteration, the result being an "improved" approximate solution to the system, x₁. We may now move on and compute the next residual vector r₁ using the formula

${\displaystyle \mathbf {r} _{1}=\mathbf {r} _{0}-\alpha _{0}\mathbf {A} \mathbf {p} _{0}={\begin{bmatrix}-8\\-3\end{bmatrix}}-{\frac {73}{331}}{\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix}-8\\-3\end{bmatrix}}={\begin{bmatrix}-0.2810\\0.7492\end{bmatrix}}.}$

Our next step in the process is to compute the scalar β₀ that will eventually be used to determine the next search direction p₁.

${\displaystyle \beta _{0}={\frac {\mathbf {r} _{1}^{\mathsf {T}}\mathbf {r} _{1}}{\mathbf {r} _{0}^{\mathsf {T}}\mathbf {r} _{0}}}={\frac {{\begin{bmatrix}-0.2810&0.7492\end{bmatrix}}{\begin{bmatrix}-0.2810\\0.7492\end{bmatrix}}}{{\begin{bmatrix}-8&-3\end{bmatrix}}{\begin{bmatrix}-8\\-3\end{bmatrix}}}}=0.0088.}$

Now, using this scalar β₀, we can compute the next search direction p₁ using the relationship

${\displaystyle \mathbf {p} _{1}=\mathbf {r} _{1}+\beta _{0}\mathbf {p} _{0}={\begin{bmatrix}-0.2810\\0.7492\end{bmatrix}}+0.0088{\begin{bmatrix}-8\\-3\end{bmatrix}}={\begin{bmatrix}-0.3511\\0.7229\end{bmatrix}}.}$

We now compute the scalar α₁ using our newly acquired p₁ using the same method as that used for α₀.

${\displaystyle \alpha _{1}={\frac {\mathbf {r} _{1}^{\mathsf {T}}\mathbf {r} _{1}}{\mathbf {p} _{1}^{\mathsf {T}}\mathbf {Ap} _{1}}}={\frac {{\begin{bmatrix}-0.2810&0.7492\end{bmatrix}}{\begin{bmatrix}-0.2810\\0.7492\end{bmatrix}}}{{\begin{bmatrix}-0.3511&0.7229\end{bmatrix}}{\begin{bmatrix}4&1\\1&3\end{bmatrix}}{\begin{bmatrix}-0.3511\\0.7229\end{bmatrix}}}}=0.4122.}$

Finally, we find x₂ using the same method as that used to find x₁.

${\displaystyle \mathbf {x} _{2}=\mathbf {x} _{1}+\alpha _{1}\mathbf {p} _{1}={\begin{bmatrix}0.2356\\0.3384\end{bmatrix}}+0.4122{\begin{bmatrix}-0.3511\\0.7229\end{bmatrix}}={\begin{bmatrix}0.0909\\0.6364\end{bmatrix}}.}$

The result, x₂, is a "better" approximation to the system's solution than x₁ and x₀. If exact arithmetic were to be used in this example instead of limited-precision, then the exact solution would theoretically have been reached after n = 2 iterations (n being the order of the system).

Convergence properties[edit]

The conjugate gradient method can theoretically be viewed as a direct method, as in the absence of round-off error it produces the exact solution after a finite number of iterations, which is not larger than the size of the matrix. In practice, the exact solution is never obtained since the conjugate gradient method is unstable with respect to even small perturbations, e.g., most directions are not in practice conjugate, due to a degenerative nature of generating the Krylov subspaces.

As an iterative method, the conjugate gradient method monotonically (in the energy norm) improves approximations ${\displaystyle \mathbf {x} _{k}}$ to the exact solution and may reach the required tolerance after a relatively small (compared to the problem size) number of iterations. The improvement is typically linear and its speed is determined by the condition number ${\displaystyle \kappa (A)}$ of the system matrix ${\displaystyle A}$: the larger ${\displaystyle \kappa (A)}$ is, the slower the improvement.^[7]

If ${\displaystyle \kappa (A)}$ is large, preconditioning is commonly used to replace the original system ${\displaystyle \mathbf {Ax} -\mathbf {b} =0}$ with ${\displaystyle \mathbf {M} ^{-1}(\mathbf {Ax} -\mathbf {b} )=0}$ such that ${\displaystyle \kappa (\mathbf {M} ^{-1}\mathbf {A} )}$ is smaller than ${\displaystyle \kappa (\mathbf {A} )}$, see below.

Convergence theorem[edit]

Define a subset of polynomials as

${\displaystyle \Pi _{k}^{*}:=\left\lbrace \ p\in \Pi _{k}\ :\ p(0)=1\ \right\rbrace \,,}$

where ${\displaystyle \Pi _{k}}$ is the set of polynomials of maximal degree ${\displaystyle k}$.

Let ${\displaystyle \left(\mathbf {x} _{k}\right)_{k}}$ be the iterative approximations of the exact solution ${\displaystyle \mathbf {x} _{*}}$, and define the errors as ${\displaystyle \mathbf {e} _{k}:=\mathbf {x} _{k}-\mathbf {x} _{*}}$. Now, the rate of convergence can be approximated as ^[4][8]

${\displaystyle {\begin{aligned}\left\|\mathbf {e} _{k}\right\|_{\mathbf {A} }&=\min _{p\in \Pi _{k}^{*}}\left\|p(\mathbf {A} )\mathbf {e} _{0}\right\|_{\mathbf {A} }\\&\leq \min _{p\in \Pi _{k}^{*}}\,\max _{\lambda \in \sigma (\mathbf {A} )}|p(\lambda )|\ \left\|\mathbf {e} _{0}\right\|_{\mathbf {A} }\\&\leq 2\left({\frac {{\sqrt {\kappa (\mathbf {A} )}}-1}{{\sqrt {\kappa (\mathbf {A} )}}+1}}\right)^{k}\ \left\|\mathbf {e} _{0}\right\|_{\mathbf {A} }\,,\end{aligned}}}$

where ${\displaystyle \sigma (\mathbf {A} )}$ denotes the spectrum, and ${\displaystyle \kappa (\mathbf {A} )}$ denotes the condition number.

Note, the important limit when ${\displaystyle \kappa (\mathbf {A} )}$ tends to ${\displaystyle \infty }$

${\displaystyle {\frac {{\sqrt {\kappa (\mathbf {A} )}}-1}{{\sqrt {\kappa (\mathbf {A} )}}+1}}\approx 1-{\frac {2}{\sqrt {\kappa (\mathbf {A} )}}}\quad {\text{for}}\quad \kappa (\mathbf {A} )\gg 1\,.}$

This limit shows a faster convergence rate compared to the iterative methods of Jacobi or Gauss–Seidel which scale as ${\displaystyle \approx 1-{\frac {2}{\kappa (\mathbf {A} )}}}$.

No round-off error is assumed in the convergence theorem, but the convergence bound is commonly valid in practice as theoretically explained^[5] by Anne Greenbaum.

Practical convergence[edit]

If initialized randomly, the first stage of iterations is often the fastest, as the error is eliminated within the Krylov subspace that initially reflects a smaller effective condition number. The second stage of convergence is typically well defined by the theoretical convergence bound with ${\displaystyle {\sqrt {\kappa (\mathbf {A} )}}}$, but may be super-linear, depending on a distribution of the spectrum of the matrix ${\displaystyle A}$ and the spectral distribution of the error.^[5] In the last stage, the smallest attainable accuracy is reached and the convergence stalls or the method may even start diverging. In typical scientific computing applications in double-precision floating-point format for matrices of large sizes, the conjugate gradient method uses a stopping criteria with a tolerance that terminates the iterations during the first or second stage.

The preconditioned conjugate gradient method[edit]

In most cases, preconditioning is necessary to ensure fast convergence of the conjugate gradient method. The preconditioned conjugate gradient method takes the following form:^[9]

${\displaystyle \mathbf {r} _{0}:=\mathbf {b} -\mathbf {Ax} _{0}}$

${\displaystyle \mathbf {z} _{0}:=\mathbf {M} ^{-1}\mathbf {r} _{0}}$

${\displaystyle \mathbf {p} _{0}:=\mathbf {z} _{0}}$

${\displaystyle k:=0\,}$

repeat

${\displaystyle \alpha _{k}:={\frac {\mathbf {r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}{\mathbf {p} _{k}^{\mathsf {T}}\mathbf {Ap} _{k}}}}$

${\displaystyle \mathbf {x} _{k+1}:=\mathbf {x} _{k}+\alpha _{k}\mathbf {p} _{k}}$

${\displaystyle \mathbf {r} _{k+1}:=\mathbf {r} _{k}-\alpha _{k}\mathbf {Ap} _{k}}$

if r_k+1 is sufficiently small then exit loop end if

${\displaystyle \mathbf {z} _{k+1}:=\mathbf {M} ^{-1}\mathbf {r} _{k+1}}$

${\displaystyle \beta _{k}:={\frac {\mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {z} _{k+1}}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}}}$

${\displaystyle \mathbf {p} _{k+1}:=\mathbf {z} _{k+1}+\beta _{k}\mathbf {p} _{k}}$

${\displaystyle k:=k+1\,}$

end repeat

The result is x_k+1

The above formulation is equivalent to applying the conjugate gradient method without preconditioning to the system^[10]

${\displaystyle \mathbf {E} ^{-1}\mathbf {A} (\mathbf {E} ^{-1})^{\mathsf {T}}\mathbf {\hat {x}} =\mathbf {E} ^{-1}\mathbf {b} }$

where

${\displaystyle \mathbf {EE} ^{\mathsf {T}}=\mathbf {M} ,\qquad \mathbf {\hat {x}} =\mathbf {E} ^{\mathsf {T}}\mathbf {x} .}$

The preconditioner matrix M has to be symmetric positive-definite and fixed, i.e., cannot change from iteration to iteration. If any of these assumptions on the preconditioner is violated, the behavior of the preconditioned conjugate gradient method may become unpredictable.

An example of a commonly used preconditioner is the incomplete Cholesky factorization.^[11]

The flexible preconditioned conjugate gradient method[edit]

In numerically challenging applications, sophisticated preconditioners are used, which may lead to variable preconditioning, changing between iterations. Even if the preconditioner is symmetric positive-definite on every iteration, the fact that it may change makes the arguments above invalid, and in practical tests leads to a significant slow down of the convergence of the algorithm presented above. Using the Polak–Ribière formula

${\displaystyle \beta _{k}:={\frac {\mathbf {r} _{k+1}^{\mathsf {T}}\left(\mathbf {z} _{k+1}-\mathbf {z} _{k}\right)}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}}}$

instead of the Fletcher–Reeves formula

${\displaystyle \beta _{k}:={\frac {\mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {z} _{k+1}}{\mathbf {r} _{k}^{\mathsf {T}}\mathbf {z} _{k}}}}$

may dramatically improve the convergence in this case.^[12] This version of the preconditioned conjugate gradient method can be called^[13] flexible, as it allows for variable preconditioning. The flexible version is also shown^[14] to be robust even if the preconditioner is not symmetric positive definite (SPD).

The implementation of the flexible version requires storing an extra vector. For a fixed SPD preconditioner, ${\displaystyle \mathbf {r} _{k+1}^{\mathsf {T}}\mathbf {z} _{k}=0,}$ so both formulas for β_k are equivalent in exact arithmetic, i.e., without the round-off error.

The mathematical explanation of the better convergence behavior of the method with the Polak–Ribière formula is that the method is locally optimal in this case, in particular, it does not converge slower than the locally optimal steepest descent method.^[15]

Vs. the locally optimal steepest descent method[edit]

In both the original and the preconditioned conjugate gradient methods one only needs to set ${\displaystyle \beta _{k}:=0}$ in order to make them locally optimal, using the line search, steepest descent methods. With this substitution, vectors p are always the same as vectors z, so there is no need to store vectors p. Thus, every iteration of these steepest descent methods is a bit cheaper compared to that for the conjugate gradient methods. However, the latter converge faster, unless a (highly) variable and/or non-SPD preconditioner is used, see above.

Conjugate gradient method as optimal feedback controller for double integrator[edit]

The conjugate gradient method can also be derived using optimal control theory.^[16] In this approach, the conjugate gradient method falls out as an optimal feedback controller,

$${\displaystyle u=k(x,v):=-\gamma _{a}\nabla f(x)-\gamma _{b}v}$$

$${\displaystyle {\dot {x}}=v,\quad {\dot {v}}=u}$$

${\displaystyle \gamma _{a}}$

${\displaystyle \gamma _{b}}$

Conjugate gradient on the normal equations[edit]

The conjugate gradient method can be applied to an arbitrary n-by-m matrix by applying it to normal equations A^TA and right-hand side vector A^Tb, since A^TA is a symmetric positive-semidefinite matrix for any A. The result is conjugate gradient on the normal equations (CGNR).

A^TAx = A^Tb

As an iterative method, it is not necessary to form A^TA explicitly in memory but only to perform the matrix-vector and transpose matrix-vector multiplications. Therefore, CGNR is particularly useful when A is a sparse matrix since these operations are usually extremely efficient. However the downside of forming the normal equations is that the condition number κ(A^TA) is equal to κ²(A) and so the rate of convergence of CGNR may be slow and the quality of the approximate solution may be sensitive to roundoff errors. Finding a good preconditioner is often an important part of using the CGNR method.

Several algorithms have been proposed (e.g., CGLS, LSQR). The LSQR algorithm purportedly has the best numerical stability when A is ill-conditioned, i.e., A has a large condition number.

Conjugate gradient method for complex Hermitian matrices[edit]

The conjugate gradient method with a trivial modification is extendable to solving, given complex-valued matrix A and vector b, the system of linear equations ${\displaystyle \mathbf {A} \mathbf {x} =\mathbf {b} }$ for the complex-valued vector x, where A is Hermitian (i.e., A' = A) and positive-definite matrix, and the symbol ' denotes the conjugate transpose using the MATLAB/GNU Octave style. The trivial modification is simply substituting the conjugate transpose for the real transpose everywhere. This substitution is backward compatible, since conjugate transpose turns into real transpose on real-valued vectors and matrices. The provided above Example code in MATLAB/GNU Octave thus already works for complex Hermitian matrices needed no modification.

See also[edit]

References[edit]

Further reading[edit]

• Atkinson, Kendell A. (1988). "Section 8.9". An introduction to numerical analysis (2nd ed.). John Wiley and Sons. ISBN 978-0-471-50023-0.
• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 978-0-486-43227-4.
• Golub, Gene H.; Van Loan, Charles F. (2013). "Chapter 11". Matrix Computations (4th ed.). Johns Hopkins University Press. ISBN 978-1-4214-0794-4.
• Saad, Yousef (2003-04-01). "Chapter 6". Iterative methods for sparse linear systems (2nd ed.). SIAM. ISBN 978-0-89871-534-7.

External links[edit]

• "Conjugate gradients, method of", Encyclopedia of Mathematics, EMS Press, 2001 [1994]