Семейные кубики Рубика разного размера

Первоначальный кубик Рубика представлял собой механический кубик 3 × 3 × 3, изобретенный в 1974 году венгерским скульптором и профессором архитектуры Эрне Рубиком . Расширения кубика Рубика существуют уже давно и представлены как в аппаратной, так и в программной форме. Основным дополнением стало появление кубов большего размера и более сложных кубов с отмеченными центрами. Свойства кубиков семейства Рубиков любого размера вместе с особым вниманием к программным кубам - вот основная тема этой статьи. Многие свойства имеют математический характер и являются функциями переменной размера куба.

Определения

В основном, используемая здесь терминология согласуется с общепринятой. В других местах некоторые термины используются в разных значениях. Чтобы избежать неправильных представлений, значения большинства терминов, используемых в этой статье, определены ниже.

Размер куба	Стандартный кубик Рубика часто называют кубом 3 × 3 × 3. Этот куб будет называться кубом размера 3 и, как правило, ${\ Displaystyle п \ раз п \ раз п}$ куб будет называться размером ${\ displaystyle n}$ куб.
Семейство кубиков рубика	Кубики, которые имеют те же вращательные свойства, что и стандартный кубик Рубика 3 размера, и подчиняются общим правилам для размера. ${\ displaystyle n}$ кубики считаются членами семейства кубиков Рубика. Доступны кубики размера 2 и выше, соответствующие этому условию.
Cubie	Отдельные элементы куба будут называться кубиками (другие иногда называют их «кублетами»). Существует три типа кубов: угловые кубы (три цветные поверхности), краевые кубы (две цветные поверхности) и центральные кубы (одна цветная поверхность). Абсолютные центральные кубы для кубов нечетного размера располагаются на центральных осях шести граней, и их относительное положение никогда не меняется.
Кабина	Кабинка - это отсек, в котором находится кубик. Для перестановки (определенной ниже) считается, что ячейки занимают фиксированные позиции в пространстве, занимаемом объектом куба, но их содержимое (кубы) может сдвигать положение.
Facelet	Грань - это видимая цветная поверхность куба (у угловых кубов есть три фасетки, у краевых кубов - две, а у центральных кубов - одна).
Кубический стиль	Здесь упоминаются два стиля куба: во-первых, стандартный куб с неотмеченными центрами, а во-вторых, куб с отмеченными центрами.
Состояние куба	Конкретное расположение кубов будет называться состоянием куба. То, что выглядит одинаково, считается одинаковым (если не указано иное). Каждое состояние имеет равную вероятность быть сформированным после подлинной случайной последовательности скремблирования. Вращение всего куба не меняет рассматриваемого здесь состояния. В других текстах различные состояния часто называют перестановками или договоренностями.
Слой куба	Слой куба - это срез куба толщиной в один кубик, перпендикулярный его оси вращения. Внешние слои (грани) содержат больше кубов, чем внутренние слои. Для куба размером ${\ displaystyle n}$ , там будет ${\ displaystyle n}$ слои вдоль любой заданной оси.
Грань куба	Значение грани куба зависит от контекста, в котором она используется. Обычно это означает один из шести трехмерных внешних слоев, но также может относиться только к поверхности внешнего слоя, которая перпендикулярна его оси вращения. Лица обычно обозначаются как вверх (U), внизу (D), спереди (F), сзади (B), слева (L) и справа (R).
Установить состояние	Установленное (или решенное) состояние куба - это такое состояние, при котором на каждой из шести граней появляется однородный цвет. Для кубов с отмеченными центрами установленное состояние характеризуется уникальным расположением всех центральных кубов, и маркировка этих кубов должна отражать это.
Зашифрованное состояние	Состояние скремблирования - это отправная точка для расшифровки куба. Он возникает, когда куб в наборе или любом другом состоянии подвергается большому количеству случайно выбранных вращений слоев.
Оси вращения «неподвижно в пространстве»	У куба есть три взаимно перпендикулярные оси вращения. Один набор осей, определенных в терминах D, U, B, F, L и R, можно рассматривать как имеющий фиксированную ориентацию в пространстве. Думайте об этих осях как о принадлежащих кубу контейнеру, в котором кубический объект может быть расположен в любой из 24 ориентаций. Одна ось может быть проведена через центры граней D и U (ось DU). Остальные - оси BF и LR.
Оси вращения «кубического объекта»	Другой набор осей может быть определен для самого объекта куба. Эти оси относятся к цветам лица, наиболее распространенными из которых являются белый, красный, оранжевый, желтый, зеленый и синий. Оси обычно бело-синие, красно-оранжевые и желто-зеленые. Для кубов нечетного размера эти оси всегда фиксированы относительно внутренней рамки объекта куба. Для кубов четного размера эти оси остаются фиксированными относительно внутренней рамки объекта куба после первоначального выбора. Начало координат осей - это центр кубического объекта.
Вращение слоя	Единственный способ изменить состояние куба - это повернуть слои куба вокруг их осей вращения. Все изменения состояния включают этапы вращения, которые можно рассматривать как последовательность четверть оборота одного слоя.
Орбита	Для базовой четверти оборота слоя куба для кубов всех размеров наборы из четырех кубиков перемещаются по отдельным траекториям с четырьмя ячейками. Когда все возможные траектории для данного типа куба рассматриваются для всего куба, мы будем ссылаться на все возможные положения движения как на заданную орбиту. Мы считаем, что куб размера 3 имеет две орбиты: одна, на которой восемь угловых кубов ограничены для движения, а другая, в которой 12 краевых кубов вынуждены двигаться. Перемещение кубов между этими орбитами невозможно. Для кубов размера 4 и выше мы также определим орбиту граничного куба как состоящую из 12 кубов, но будем использовать термин дополнительная орбита для описания пары орбит, между которыми могут перемещаться граничные кубы. Пара дополнительных реберных кубических орбит содержит всего 24 куба. Кубы размера 4 и выше включают центральные кубические орбиты, содержащие 24 куба. Перенос кубиков с одной такой орбиты на другую невозможен (относится к кубам размером 5 и выше).
Двигаться	Движение - это поворот на четверть оборота слоя или последовательность таких четверть оборота, которые человек может применить как один шаг.
Обозначение перемещения	Четверть оборота по часовой стрелке внешнего слоя обычно обозначают буквами U, D, F, B, L или R. В остальном используемые обозначения различаются между авторами. Например, четверть оборота против часовой стрелки внешнего слоя можно выразить как U ', D', F ', B', L 'или R'.
Алгоритм	Алгоритм определяет последовательность поворотов слоев для преобразования данного состояния в другое (обычно менее скремблированное) состояние. Обычно алгоритм выражается в виде печатаемой последовательности символов в соответствии с некоторыми обозначениями хода. Алгоритм можно считать «умным» ходом. Все алгоритмы - это ходы, но несколько ходов считаются алгоритмами.
Перестановка	Перестановка куба, как здесь используется, означает акт перестановки (то есть перестановки) положений кубов. Перестановка - это всеобъемлющий термин, который включает в себя последовательность четвертей оборота любой длины. Даже решение куба из зашифрованного состояния представляет собой перестановку. Термин «перестановка» широко используется математиками, которые используют теорию групп для количественной оценки процесса перестановки кубов. Термин «перестановка» также часто используется для обозначения состояния куба, которое возникает после его перестановки, но это значение здесь использоваться не будет. В таких случаях будет использоваться термин «состояние куба». Это позволяет использовать термин «перестановка», когда перестановка не приводит к изменению состояния - область, представляющая особый интерес для перестановок кубиков семейства Рубика.
Паритет	Перестановка куба может быть представлена несколькими перестановками двух кубов. Если это число четное, перестановка имеет четность, а если число нечетное, перестановка имеет нечетную четность.

Типы кубов

Аппаратные кубики

Аппаратные (физические) кубы основаны на оригинальном кубе размера 3, изобретенном Эрно Рубиком в 1974 году. Эти кубики обычно используют цветные наклейки на гранях для идентификации куба. В размере 3 куб получили пик интерес стандартного Рубика в 1980 - х годах и был тесно следует размером 4 (Месть Рубика) куб. Другие, обычно доступные в последнее время, аппаратные формы куба имеют размер 2 (карманный куб), размер 5 (куб профессора), размер 6 (V-куб 6) и размер 7 (V-куб 7). Также были произведены менее известные аппаратные кубы больших размеров. В настоящее время самый большой производимый аппаратный куб имеет размер 33, а самый крупный серийный куб - размер 19. ^[1]

Кубы программного обеспечения

Параллельно с аппаратной формой куба доступно множество программных форм, которые подчиняются тем же правилам, что и аппаратные формы. Эмуляторы программных кубов не подчиняются физическим ограничениям, которые накладывают ограничение на размер аппаратных форм. Следовательно, единственные действительно большие доступные кубы - это кубики в программной форме. Кроме того, в отличие от аппаратных форм, с помощью одной программы можно легко приспособить кубы различных размеров. Конструктивные характеристики программ, которые позволяют пользователям расшифровывать кубы, значительно различаются, при этом часто доступны такие функции, как возможность позволять пользователю сохранять частично расшифрованное состояние.

Программные кубы использовались в 1980-х годах, когда широко использовались монохромные мониторы. Отсутствие цвета означало, что требовался другой способ идентификации лица. Программа , которая сохраняется возможность монохромной 1980 - х лет (используя цифры от 1 до 6 , чтобы идентифицировать Facelets) для кубов в размере от 2 до 11 диапазона была получена в 1991 году (вместе с возможностью цвета размера от 2 до 15 диапазона). В недавно разработанных программных кубах используются цветные лицевые панели, как в аппаратных кубах.

Наиболее распространенный, но ни в коем случае не универсальный подход - имитировать куб, предоставляя «трехмерное» отображение куба, которое делает его похожим на настоящий аппаратный куб. Недостатком «трехмерного» отображения является то, что без некоторых дополнительных улучшений состояние частей куба для любого данного вида скрыто.

Некоторые программисты также используют другие подходы к интерактивному программному обеспечению, которые не имитируют трехмерный куб. Как правило, цель таких подходов состоит в том, чтобы обеспечить постоянное наблюдение за состоянием всех кубов, но имеет недостаток (для некоторых зрителей), заключающийся в том, что отображение не выглядит как реальный куб. Один из подходов - это обычное двухмерное (развернутое) отображение, в котором все элементы куба имеют одинаковый размер. Также используется другая форма отображения, при которой все элементы куба не имеют равного размера. Верхний предел размера куба программного обеспечения ограничен доступными пикселями монитора и тем, что зрители считают приемлемым, что, в свою очередь, является функцией их остроты зрения. Для кубов большого размера может быть выгодно разрешить прокрутку части куба за пределами поля зрения.

Все эмуляторы предоставляют пользователю средства для пошагового изменения состояния куба и его расшифровки. Большинство эмуляторов используют движения мыши для управления вращением элементов куба, другие используют команды клавиатуры, а некоторые используют их комбинацию.

Программные кубы предоставляют некоторые основные возможности, которые невозможны с аппаратными кубами. Всегда доступен мгновенный возврат в заданное состояние. Если программа позволяет сохранить частично расшифрованное состояние, то, регулярно обновляя сохраненное состояние, пользователям не нужно отчаиваться, если они делают что-то, что оставляет их куб в беспорядке. Они могут вернуться к ранее записанному состоянию и продолжить оттуда. Чем больше куб, тем полезнее становится такая возможность.

Доступны некоторые бесплатные реализации больших кубов (размер больше 10) .

Варианты дизайна куба

Хотя существует несколько используемых вариантов, здесь будут рассмотрены только два:

Стандартные кубики с немаркированным центром.
Кубики с отмеченными центрами.

Стандартные кубы с немаркированным центром

Двухслойный куб (размер 2) имеет только угловые кубы.

Кубы размера 2 и размера 3 имеют единое решение, что означает, что все элементы куба могут иметь только одно правильное местоположение для решенного куба.

Центральные кубы отличаются от угловых и краевых кубов тем, что их ориентация или положение имеют несколько возможностей. Для кубов нечетного размера будет центральный куб, расположенный по центру на грани куба, и у этого куба есть только одно правильное местоположение для решенного куба. Однако для решенного куба применяется несколько местоположений всех остальных центральных кубов. Центральные кубы (кроме единственного центрального куба нечетного размера) образуют наборы из четырех на каждой грани и наборы из 24 для всего куба для различных орбит. Эти центральные кубы имеют четыре возможных конечных положения (их ориентация меняется вместе с положением, но не может быть изменена независимо), которые удовлетворяют решенному состоянию.

Кубики с отмеченными центрами

Как правило, аппаратные кубы с отмеченными центрами используют изображения или логотипы на гранях, чтобы указать, какая ориентация центрального куба (ов) требуется для решенного куба. Такие кубы также называют «суперкубами», и нанесение маркировки этого типа обычно ограничивается кубиками очень маленького размера.

Сборка куба с отмеченными центрами значительно сложнее, чем для стандартных кубов. Использование разметки изображения лобзиком на кубах большого размера сделало бы трудную задачу еще более сложной. В настоящее время на программных кубах используются две возможности: использование числовой графики в диапазоне от «1» до «4» и использование графической маркировки углов.

Между числовой и угловой маркировкой существует прямое соответствие. Маркировка квадранта в верхнем левом углу эквивалентна цифровой маркировке 1, второй квадрант - 2, третий квадрант - 3 и четвертый квадрант - 4. Следующее изображение иллюстрирует эти различные формы маркировки.

Поскольку перемещение кубов между орбитами невозможно, для каждой орбиты можно использовать одинаковые отметки 1-2-3-4. За исключением абсолютных центральных кубов для кубов нечетного размера, на каждой орбите имеется 24 центральных куба (по 4 на грань). Если ${\ displaystyle n}$ размер куба, будет ${\ displaystyle {\ frac {\ left (n-2 \ right) ^ {2} -a} {4}}}$ орбиты, где ${\ displaystyle a}$ равно нулю, если ${\ displaystyle n}$ даже или ${\ displaystyle a}$ один, если ${\ displaystyle n}$ странно.

Цифровая маркировка обычно применяется для кубов размером примерно до 32. Угловая маркировка, хотя и менее удобна для пользователя, может позволить расширить диапазон отмеченных центров за пределы числовой маркировки.

За исключением разметки абсолютного центра для кубов нечетного размера, числовая разметка является лучшим средством разметки центрального куба для аппаратных кубов, поскольку диапазон их размеров ограничен. Вращение чисел будет означать небольшое неудобство по сравнению с неповорачиваемыми числами, которые можно использовать для программных кубов. Большим преимуществом чисел является то, что они уменьшают сложность решения последней грани куба, когда используются разметки (например, если последовательность из четырех чисел составляет 1-3-4-2 (даже при четности, требуется два перестановки, чтобы стать требуется 1-2-3-4), то требования к алгоритму ясны.Алгоритмы определены в ^[2] и, конечно же, в равной степени применимы к аппаратным кубам.

Правила для кубиков семьи Рубика

Куб является разрешимым, если установленное состояние существовало некоторое время в прошлом и если не произошло никакого вмешательства в куб (например, путем перестановки наклеек на аппаратных кубах или путем выполнения аналогичных действий в программных кубах). Были задокументированы правила для кубика Рубика стандартного размера 3 ^[3]^[4] и для всего семейства кубиков Рубика ^[5] . Эти правила ограничивают возможные варианты расположения и означают, что из возможных неограниченных расположений кубов число недостижимых намного превышает число доступных.

Кубики всех размеров имеют три взаимно перпендикулярные оси, вокруг которых можно вращать один или несколько слоев. Все движения куба можно рассматривать как последовательность четвертьоборотных вращений вокруг этих осей. Возможности движения порождают набор правил (или законов), которые в большинстве случаев могут быть выражены в аналитических терминах.

Для куба размером ${\ displaystyle n}$ :

Количество угловых кубиков	${\ displaystyle 8}$
Количество граничных кубов	${\ Displaystyle 12 \ влево (п-2 \ вправо)}$
Количество центральных кубов	${\ Displaystyle 6 \ влево (п-2 \ вправо) ^ {2}}$
Количество фацетов	${\ displaystyle 6n ^ {2}}$
Общее количество кубиков	${\ Displaystyle 6 \ влево (п-1 \ вправо) ^ {2} +2}$
Увеличение общего количества кубов на единицу увеличения размера куба с ${\ displaystyle n}$ к ${\ Displaystyle \ влево (п + 1 \ вправо)}$	${\ displaystyle 12n-6}$

Каждое движение куба можно рассматривать как перестановку. Связь между состоянием куба после хода и состоянием перед ходом можно математически выразить с помощью теории групп ^[6]^[7]^[8]для количественной оценки перестановок. Поскольку каждое движение можно рассматривать как последовательность четвертьоборотных вращений, уместно исследовать, что входит в четвертьоборотные вращения. За исключением абсолютного центрального куба для кубиков нечетного размера, во время четверти оборота кубики перемещаются по отдельным траекториям с четырьмя ячейками (также называемое четырехцикловым движением, поскольку четыре четверти оборота вернут кубики по указанной траектории в их исходное положение. ). Четверть оборота комплекта из 4 кубов может быть представлена тремя перестановками, как показано ниже, где подстановка 1-2 означает, что содержимое ячейки 1 заменяется содержимым ячейки 2 и т. Д.

Начинать
1 / А	2 / В
4 / Д	3 / С

Обмен 1-2
B	А
D	C

Обмен 1-3
C	А
D	B

Обмен 1-4
D	А
C	B

Четность ^[9] перестановки указывает, является ли эта перестановка четной или нечетной. Четная перестановка - это такая перестановка, которая может быть представлена четным числом перестановок, а нечетная перестановка - это перестановка, которая может быть представлена нечетным количеством перестановок. Нечетная перестановка, за которой следует нечетная перестановка, будет представлять общую четную перестановку (добавление двух нечетных чисел всегда возвращает четное число). Поскольку четверть оборота состоит из ряда 4-х циклов, каждый из которых включает три перестановки, если количество 4-х циклов нечетное, общая четность перестановки четверть оборота будет нечетной, и наоборот.

Четвертьоборотный паритет перестановки для размера ${\ displaystyle n}$ куб приведен в следующей таблице.

Размер куба (четный или нечетный)	Тип слоя	Количество 4-тактных движений	Общий паритет
странный	внутренний	${\ displaystyle n-1}$	даже
странный	внешний	${\ Displaystyle {\ гидроразрыва {\ влево (п-2 \ вправо) ^ {2} -1} {4}} + \ влево (п-1 \ вправо)}$	даже ^[а]
даже	внутренний	${\ displaystyle n-1}$	странный
даже	внешний	${\ displaystyle \ left ({\ frac {n} {2}} - 1 \ right) ^ {2} + \ left (n-1 \ right)}$	даже если ${\ displaystyle {\ frac {n} {2}}}$ даже ^[b] странно, если ${\ displaystyle {\ frac {n} {2}}}$ странно
^ Поскольку ${\ Displaystyle \ влево (п-2 \ вправо) ^ {2} -1}$ равно ${\ Displaystyle \ влево (п-1 \ вправо) \ влево (п-3 \ вправо)}$ , произведение двух последовательных четных чисел, которые всегда должны делиться на 8 без остатка. ^ Поскольку ${\ displaystyle \ left ({\ frac {n} {2}} - 1 \ right) ^ {2}}$ будет странно, если ${\ displaystyle \ left ({\ frac {n} {2}} - 1 \ right)}$ нечетное (т.е. если ${\ displaystyle {\ frac {n} {2}}}$ является четным), что дает в целом даже с тех пор, как ${\ Displaystyle (п-1)}$ странно. Обратное верно, если ${\ displaystyle {\ frac {n} {2}}}$ странно.

Обобщая приведенные выше результаты паритета, мы делаем вывод:

Все перестановки для кубов нечетного размера имеют четную общую четность.
Все отдельные четверти оборота для кубов четного размера, где половина размера куба является нечетным числом, имеют общую нечетную четность.
Для кубов четного размера, где половина размера куба является четным числом, четверть оборота внутреннего слоя имеют нечетную общую четность, а четверть витков внешнего слоя имеют четную общую четность.

В приведенном выше анализе учитывалась четность для угловых (где применимо), краевых и центральных кубов вместе взятых. Их можно рассматривать изолированно, и когда это будет сделано, четная комбинированная четвертьоборотная четность будет включать ряд нечетных элементов четности.

Стандартные кубы (т. Е. Кубы с немаркированным центром) любого размера больше 3 ведут себя точно так же, как куб размера 3, если разрешено только вращение внешнего слоя. Правила четности диктуют, что для кубов нечетного размера замена двух кубов в одном наборе ребер требует изменения положения центральных кубов. Можно показать ^[5], что для куба размера 4 замена и инвертирование двух дополнительных кубов в одном наборе ребер может быть достигнута без каких-либо изменений положения любых других кубов. Также можно показать, что для кубов четного размера 6 и выше замена двух кубов в одном наборе ребер требует изменения положения центральных кубов.

Используемая здесь перестановка учитывает изменение положения кубов, а не изменение их ориентации. Для 24-х сторонних наборов кубов (состоящих из 12 дополнительных пар) ограничений по положению нет. Ориентация устанавливается позицией и не может быть изменена независимо от позиции.

Угловые кубики ведут себя одинаково для кубиков всех размеров. У них есть три возможных ориентации, состоящих из комбинации ${\ displaystyle {\ frac {1} {3}}}$ скручивания, когда полный поворот (вокруг оси, проведенной от угла куба к внутреннему углу куба) возвращает угловой куб в его исходную ориентацию. Если обозначить единицу поворота по часовой стрелке как ${\ displaystyle {\ frac {1} {3}}}$ и поворот против часовой стрелки на ${\ displaystyle - {\ frac {1} {3}}}$ , то возможности поворота углового куба относительно любого заданного начального состояния (например, заданного состояния) равны 0, ${\ displaystyle {\ frac {1} {3}}}$ и ${\ displaystyle - {\ frac {1} {3}}}$ . Сумма приращений скручивания по всем угловым кубам всегда должна быть целым числом (0, 1 или 2).

Когда вращение внутреннего слоя включено для кубов размером больше 3, некоторые из упомянутых выше ограничений перемещения кубов по краям больше не применяются. Они подробно описаны в разделе « Проблемы последнего уровня ».

Положение и ориентация куба имеют особое значение при расшифровке последнего слоя. Перед скремблированием граничные кубы всегда должны находиться в тех же позициях, которые они занимали в исходном установленном состоянии. Если какой-либо реберный куб в данном наборе ребер на последнем слое имеет неправильную ориентацию (применимо только к кубам размером больше 3), он должен быть в неправильном положении и его нужно будет заменить на дополнительный реберный куб, также имеющий неправильную ориентацию. ориентация. При наличии всего остального угловые кубы могут быть в правильном положении, но два или более могут иметь неправильную ориентацию. Для стандартных кубов размером больше 3 существует незначительная вероятность того, что центральные кубы (кроме абсолютных центральных кубов для кубов нечетного размера) будут занимать те же позиции, что и в исходном заданном состоянии (при условии, что центральные кубы не помечены).

Кубы четного и нечетного размера с отмеченными или немаркированными центрами подчиняются правилу: «Любая перестановка, которая приводит только к перестановке центральных кубов на 24 кубических орбитах, должна иметь четность».

Если рассматриваются перестановки граней, а не кубов, то во внимание будут приниматься как положение, так и ориентация кубов. Для программных кубов состояния (шесть цветовых вариантов) ${\ displaystyle 6n ^ {2}}$ лица (в ${\ Displaystyle 6 \ раз п \ раз п}$ array) - это то, что позволит сохранить полную информацию о состоянии куба для дальнейшего использования.

Куб любого размера, который подвергается повторениям одной и той же перестановки, в конечном итоге вернется в состояние (например, установленное состояние), которое он занимал до первого применения перестановки. ^[6]^[7] Количество раз, которое необходимо применить перестановку для первого возврата куба в его начальное состояние, называется порядком или длиной цикла перестановки и применимо к кубам любого размера. Общая перестановка, которая не приводит к изменению состояния, называется перестановкой идентичности. Доступна программа, которая позволяет определять длину цикла перестановки куба любого размера ^[10], а результаты длины цикла выборки задокументированы. ^[5] Для данной перестановки длина цикла может варьироваться в зависимости от:

Размер куба.
Исходное состояние куба (для стандартных кубов с немаркированным центром).
Стиль куба (используются стандартные или отмеченные центры).
Пространственная ориентация (проверка всех 24 из них, а не только одного, может дать другой результат).

Четность перестановки идентичности всегда четная. Этот результат для кубиков нечетного размера, очевидно, верен, поскольку каждая четверть оборота имеет четность. Для кубиков одинакового размера результат менее очевиден. Для кубов четного размера, если перестановка скремблирования относительно предыдущего состояния набора является нечетной, то любая перестановка для решения куба также должна иметь нечетную четность, и наоборот.

Обобщенное количество возможных состояний для размера ${\ displaystyle n}$ куб считается в разделе « Достижимые состояния для кубов всех размеров ».

Решение куба

Решение людей

Решение куба включает в себя начало со скремблированным кубом и применение пошаговых поворотов слоев, чтобы в конечном итоге получить решенный куб. Для кубов с немаркированным центром это означает, что все грани должны иметь одинаковый цвет. Для кубов с отмеченными центрами необходимо будет применить уникальное расположение всех центральных кубов в дополнение к требованию единообразного цвета. Поскольку начальная точка всегда разная, никогда не может быть уникального набора поворотов, который можно было бы применить для сборки куба. Обычно люди работают над решением с возможным использованием алгоритмов , в основном на последней стадии дескремблирования. Теоретически человек может написать компьютерную программу, которая «думает» как человек и решает куб без вмешательства человека (см. Раздел « Решение с помощью компьютерной программы»). раздел).

Цель большинства программных эмуляторов куба - предоставить пользователю средства для взаимодействия с программой для решения (расшифровки) куба аналогично тому, как они бы расшифровывали аппаратный куб.

Эффективные последовательности вращения (алгоритмы) могут быть разработаны с использованием математики перестановок теории групп. Однако есть много ссылок на соответствующие последовательности вращения, необходимые для решения кубов небольшого размера (см. Некоторые для кубов размером 3, 4 и 5 ^[11]^[12]^[13]^[14] ), и существует несколько подходов к какие шаги можно использовать. Не существует неправильного способа собрать куб. Шаги, необходимые для решения любого куба размера больше 4, являются довольно простыми расширениями шагов, необходимых для решения кубов размера 3 и 4. Однако существует ограниченное количество обобщенных инструкций, которые можно применить для решения кубов любого размера (особенно больших). Обобщенное руководство по одному из способов решения стандартных кубов ^[15]и кубики с отмеченным центром ^[2] всех размеров доступны.

Любой, кто может собрать куб размером 4, должен иметь возможность собирать кубы большего размера при условии, что он принимает увеличенный штраф за время решения. Функции разработки программного обеспечения, недоступные в аппаратных кубах, могут упростить процесс решения куба. Для данного набора конструктивных особенностей куба сложность (сложность) решения куба семейства Рубика увеличивается, если количество достижимых состояний увеличивается. На это число влияют три основных свойства:

Размер куба: количество кубиков, которые необходимо разместить, является квадратичной (полиномиальной второго порядка) функцией размера куба и, следовательно, имеет большое влияние на сложность решения куба.
Нечетный или четный размер: кубы четного размера имеют дополнительный эффект по сравнению с размером куба, что добавляет сложности по сравнению с кубами нечетного размера. Этот эффект относительно невелик и не зависит от размера куба (дополнительный вклад, когда размер куба изменяется от ${\ displaystyle n}$ к ${\ Displaystyle \ влево (п + 1 \ вправо)}$ для ${\ displaystyle n}$ нечетное постоянное). Этот эффект будет расширен, когда позже будет рассмотрено количество достижимых состояний.
Неотмеченные или отмеченные центральные кубы. Маркировка центрального куба усложняет решение кубов.

Были определены дополнительные алгоритмы для помощи пользователям в решении куба размера 3 ^[16] и куба любого размера ^[2] с отмеченными центрами.

Проблемы с большими кубами

Доступны эмуляторы больших кубов, предназначенные для кубов размером до 100 и более. Независимо от заявленного верхнего предела размера доступные пиксели (которые различаются в зависимости от используемого монитора) и острота зрения пользователя накладывают практические ограничения на максимальный размер куба, с которым может справиться человек.

Как указано в разделе « Правила игры в кубики семьи Рубика» , общее количество кубиков равно ${\ Displaystyle \ влево \ {6 \ влево (п-1 \ вправо) ^ {2} +2 \ вправо \}}$ , а количество центральных кубов равно ${\ Displaystyle 6 \ влево (п-2 \ вправо) ^ {2}}$ , куда ${\ displaystyle n}$ размер куба. Для кубиков большого размера количество центральных кубиков становится очень важным, как показано ниже.

Размер куба:	4	8	16	32	64
Всего кубов:	56	296	1352	5768	23816
Доля центрального куба от общего количества кубов (%):	42,8	73,0	87,0	93,6	96,8

Отсюда следует, что размещение центральных кубов будет становиться все более значимым, чем размещение других кубов, по мере увеличения размера куба. Время, необходимое для сборки куба, резко возрастает с увеличением размера куба. Например, в куб размером 16 нужно разместить примерно в 24 раза больше кубов, чем в кубе размера 4. Если бы среднее время для установки куба было одинаковым в обоих случаях, этот множитель 24 также применился бы. Фактор 24, вероятно, будет заниженным, потому что наличие большого количества кубов затрудняет (и требует времени) определение того, что и где принадлежит.

Создать программу, позволяющую изменять состояние кубов большого размера, не намного сложнее, чем сделать то же самое для кубиков небольшого размера. Однако решение больших кубов - гораздо более сложная и трудоемкая задача, чем то же самое для маленьких кубиков. Следовательно, вероятно, что большинство действительно больших программных кубов, которые доступны, так и не были решены.

Определение точных местоположений для поиска кубиков (в основном, четырехместных центральных кубов) является серьезной проблемой для больших кубов. Использование вторичной сетки маркеров ^[10] может облегчить идентификацию. Например, можно использовать маркерную сетку для формирования 4 × 4 сегментов для куба размером 16 (16 таких сегментов на грань).

Общий набор из шести цветов кубов, принятых как для кубов оборудования, так и для кубов программного обеспечения, включает белый, красный, оранжевый, желтый, зеленый и синий. Этот набор цветов может быть неоптимальным для программных кубов большого размера, где количество пикселей на кубик мало. Например, различие между белым и желтым может быть проблематичным. Уменьшение количества цветов в диапазоне от красного до синего с пяти до четырех и добавление фиолетового (цвет на границе видимого спектра ) дает набор цветов, который можно считать более подходящим для кубиков большого размера. Некоторые реализации программных кубов позволяют пользователям при желании изменять набор цветов по умолчанию. Это полезное дополнение для пользователей, у которых цветовое восприятие не соответствует норме.

Решение компьютерной программой

Решение куба с помощью компьютерной программы ^[17] (в отличие от обычного способа, которым люди решают куб) для кубов небольшого размера (например, размера 3) было разработано, и столь же легко решать кубы большого размера на компьютере.

Проблемы с последним слоем

«Проблема последнего слоя» определяется здесь, чтобы означать необходимость перестановки кубов края последнего слоя, что не может быть достигнуто с помощью движений куба стандартного размера 3. Их часто называют проблемами четности или ошибками, но такая терминология может вводить в заблуждение. Если бы ходы были ограничены теми, которые доступны для куба размера 3, такие состояния были бы недоступны (нарушить правила четности). Существует множество вариантов представления проблем конечного слоя и алгоритмов их решения, но требования к исправлению будут аналогичны описанным ниже. Рассмотренные здесь проблемы в равной степени применимы как к стандартным кубам, так и к кубам с отмеченными центрами, но в последнем случае возникают дополнительные проблемы с конечным слоем для выравнивания центральных кубов.Задачи для больших кубов можно рассматривать как прямое продолжение тех, которые относятся к кубу размера 4. В основном могут возникнуть проблемы двух типов:

Необходимо перевернуть дополнительную пару или полный набор реберных кубов в окончательном наборе ребер. Это условие будет называться требованием OLL (ориентация последнего слоя).
На последнем слое необходимо поменять местами два набора кубиков с краями. Это условие будет называться требованием PLL (перестановка последнего уровня).

OLL и PLL, используемые здесь, можно рассматривать как подмножества обычных определений этих терминов. Есть много ссылок на ходы, которые можно использовать для решения этих проблем. Меньшее количество ссылок ^[5]^[18] демонстрирует, как эти ходы удовлетворяют правилам четности. С точки зрения четности необходимо учитывать перестановку центральных кубов, которую нелегко наблюдать в кубах с неотмеченными центрами. Здесь будет проиллюстрировано только соответствие OLL четности.

Показана типичная поправка OLL для куба размера 9. Цветные кубики - единственные в кубе, которые меняют положение.

OLL до коррекции на размер 9 куб.

OLL после коррекции на размер 9 куб.

Для коррекции OLL есть ${\ displaystyle n-2}$ свопы центрального куба и в целом есть ${\ Displaystyle \ влево (п-1 \ вправо)}$ меняет местами при включении пары ребер. Для кубиков нестандартного размера ${\ Displaystyle \ влево (п-1 \ вправо)}$ всегда четный (и соответствует универсальному требованию четности для кубов нечетного размера). Для кубиков равного размера ${\ Displaystyle \ влево (п-1 \ вправо)}$ всегда является нечетным, что означает, что в этом случае всегда происходит изменение четности, допустимое условие четности для кубов четного размера.

Для полного переворота набора ребер (требование, которое может возникнуть только для кубиков четного размера) количество перестановок будет равно ${\ Displaystyle \ влево (п-1 \ вправо) \ влево ({\ гидроразрыва {п} {2}} - 1 \ вправо)}$ . Общее количество свопов будет, даже если ${\ displaystyle \ left ({\ frac {n} {2}} - 1 \ right)}$ четное (т.е. ${\ displaystyle {\ frac {n} {2}}}$ нечетно). Общее количество свопов будет нечетным, если ${\ displaystyle {\ frac {n} {2}}}$ даже. Следовательно, общий паритет будет, даже если ${\ displaystyle {\ frac {n} {2}}}$ является нечетным и нечетным, если ${\ displaystyle {\ frac {n} {2}}}$ даже.

Четность данного алгоритма, конечно, также может быть выведена из его содержимого, используя правила, подробно описанные в разделе « Правила для кубиков семейства Рубика» .

Для стандартных кубов перестановка центральных кубов для решения проблем OLL и PLL не важна. Для кубов с отмеченными центральными кубами эффект такой перестановки этих кубов является серьезным недостатком. Для кубов с отмеченными центрами невозможно (за исключением куба размера 4) выровнять все центральные кубы последнего слоя до тех пор, пока все краевые кубы не будут помещены в свои окончательные положения.

Алгоритмы

Инструкции для людей о том, как решать кубики типа Рубика, обычно передаются либо в чисто графической форме, либо в виде последовательностей, определенных с использованием печатной записи символов. Последовательность символов, которую можно транслировать и применять для выполнения последовательности вращений слоев для преобразования заданного состояния в другое (обычно менее скремблированное) состояние, часто называют алгоритмом.. Алгоритмы наиболее часто используются при дескремблировании последней части куба, но при желании могут применяться более широко. Алгоритмы можно записать в виде инструкций, которые можно запомнить или просмотреть в документе. Используемые печатаемые символы (например, для обозначения четверти оборота против часовой стрелки, четверть оборота одного слоя или четверть оборота многослойного) в инструкциях алгоритма различаются среди авторов, как и их положение в инструкциях. Когда люди интерпретируют инструкции так, как они представлены, это не имеет значения. Единственный раз, когда форма представления имеет значение, - это когда ввод с клавиатуры компьютера используется для изменения состояния программных кубов, а автоматическое обновление изображения на экране происходит всякий раз, когда принимается действительная инструкция. Например, если F 'используется для обозначения поворота передней грани на четверть против часовой стрелки,затем, когда пользователь вводит F, будет происходить четверть оборота по часовой стрелке, и потребуется корректировка, когда пользователь наберет символ '. Конечный результат все равно будет правильным, но использование -F вместо F устранит лишнее вращение. Следует избегать любых улучшений текста, таких как надстрочные или подстрочные индексы, в методе представления последовательностей вращения кубов, когда пользователи общаются с программными кубами с помощью команд клавиатуры. Когда используется ввод инструкций с клавиатуры компьютера,Следует избегать в методе представления последовательностей вращения куба, когда пользователи общаются с программными кубами с помощью команд клавиатуры. Когда используется ввод инструкций с клавиатуры компьютера,следует избегать в методе представления последовательностей вращения куба, когда пользователи общаются с программными кубами с помощью команд клавиатуры. Когда используется ввод инструкций с клавиатуры компьютера,макросы (которые отображают короткую текстовую строку ввода в более длинную строку) могут использоваться ^[10]^[15]^[19] как ярлыки алгоритмов.

Время собирать кубики

Спидкубинг (или спидкубинг) - это практика решения куба из семейства кубиков Рубика за максимально короткое время (что обычно подразумевает сокращение количества требуемых ходов на четверть оборота). Чаще всего он применяется к кубам небольшого размера, и существует множество задокументированных методов решения. Международная группа исследователей, использующих компьютерную мощь Google, нашла все способы решения кубика Рубика стандартного размера 3 и показала, что можно завершить решение за 20 ходов или меньше ^[20] для любого начального зашифрованного состояния (где движение здесь определяется как четверть или пол-оборота лица). Как правило, методы быстрого решения применимы больше к специалистам-кубистам, чем к типичным кубистам, и они более сложны, чем простые методы послойного набора, используемые большинством других людей.

Доступные и недоступные состояния для кубов всех размеров

Если куб в какой-то момент ранее занимал заданное состояние, то любое состояние, которое может возникнуть после разрешенных ходов, считается достижимым состоянием. Для кубиков небольшого размера (размер 2, 3 или 4) недостижимое состояние - это состояние, которое не может быть достигнуто с помощью разрешенных ходов. Для кубов большего размера необходимо дополнительное уточнение того, что подразумевается под недостижимым состоянием. В этой статье исключается условное перемещение между 24-кубовыми орбитами для ребер и для центральных кубов.

Связь между достижимым и недостижимым состояниями

Если для куба любого размера m представляет количество достижимых состояний, u представляет количество недостижимых состояний, а t равно их сумме:

{\ Displaystyle т = и + м}

{\ displaystyle t = km}

куда

{\ displaystyle k}

положительное целое число

{\ Displaystyle и = \ влево (к-1 \ вправо) м}

И m, и k являются функциями размера куба ${\ displaystyle n}$ . Значения m и k будут рассмотрены в следующих разделах. В других текстах «достижимые состояния» часто называют «перестановками».

Доступные состояния для кубов всех размеров

Количество достижимых состояний основано на:

Математика стандартных перестановок и комбинаций . ^[21]
Коэффициенты уменьшения, которые должны быть применены к вышеупомянутому, отражают ограничения движения, характерные для кубиков семейства Рубика.

Количество различных состояний, которые достижимы для кубов любого размера, можно просто связать с числами, которые применимы к кубам размера 3 и размера 4. Хофштадтер в своей статье 1981 г. ^[22] представил полный вывод числа состояний для кубика Рубика стандартного размера 3. Также доступны более свежие источники информации, которые адекватно подтверждают цифры для кубов размера 3 ^[3]^[4]^[23] и размера 4 ^[24] . Ссылки, указывающие количество возможных состояний для размера ${\ displaystyle n}$ куб доступны. ^[24]^[25]^[26] Краткий материал, представленный ниже, представляет результаты в форме, использованной в одной из этих ссылок ^[24], которая освещает тему гораздо более подробно.

Для кубов с неотмеченными центральными кубами применяются следующие положительные целочисленные константы (представленные P, Q, R и S). Эти константы согласуются с цифрами, которые часто приводятся для кубов размера 3 и 4.

Возможности углового куба для кубов одинакового размера	п	(7!) 3 ⁶	3.67416000000000 × 10 ⁶
Возможности кубиков с центральным краем для кубов нечетного размера, умноженные на 24	Q	24 (12!) 2 ¹⁰	1,17719433216000 × 10 ¹³
Возможности Edge Cubie для каждого двойного набора (12 пар)	р	24!	6.20448401733239 × 10 ²³
Возможности центрального куба для каждого четверного набора (6 групп по 4)	S	(24!) / (4!) ⁶	3,24667053711000 × 10 ¹⁵
Примечание: ! является факторный символ (N! означает продукт 1 × 2 × ... × N).

Значение S может потребовать слов пояснения, поскольку обычно предполагается, что количество возможных состояний для центральных кубов с опознавательными метками для куба размера 4 равно 24 !. Использование этого значения гарантированно даст неправильный ответ, если рассматриваются кубы с отмеченным центром. Первые 20 кубиков могут быть размещены произвольно, что дает коэффициент 24! / 4 !. Однако для каждого возможного расположения реберных кубиков только половина из 4! гипотетические договоренности для последних четырех достижимы. ^[2]^[24] Следовательно, правильное значение для куба с отмеченными центрами - 24! / 2. Если маркировка удалена, применяется «перестановка с некоторыми идентичными объектами» ^[21] . Для стандартного куба отмеченное значение куба необходимо разделить на (4!) ⁶/ 2 (здесь также должен применяться 2-й делитель). Это дает общее значение S для куба размера 4, равное 24! / (4!) ⁶ . Все состояния для орбит с 24 центрами куба для стандартных кубиков семейства Рубика достижимы (при необходимости, даже четность всегда достижима, поменяв местами пару центральных кубов одного цвета).

{\ displaystyle m = {\ textrm {P}} {\ textrm {Q}} ^ {a} {\ textrm {R}} ^ {b} {\ textrm {S}} ^ {c}}

куда

{\ displaystyle a}

,

{\ displaystyle b}

, и

{\ displaystyle c}

положительные целые переменные (функции размера куба

{\ displaystyle n}

), как указано ниже.

{\ displaystyle a = n {\ textrm {mod}} 2}

(т.е. 0, если

{\ displaystyle n}

равно или 1, если

{\ displaystyle n}

странно)

{\ displaystyle b = {\ frac {n-2-a} {2}}}

{\ displaystyle c = {\ frac {\ left (n-2 \ right) ^ {2} -a} {4}}}

Для кубиков равного размера ${\ displaystyle {\ textrm {Q}} ^ {a} = 1}$ (см. возведение в степень ).

Для дальнейшего упрощения параметр ${\ displaystyle m}$ также может быть выражено как ${\ displaystyle m = 10 ^ {y}}$ куда ${\ displaystyle y = {\ textrm {log}} _ {10} m}$ . Параметр ${\ displaystyle y}$ может быть связано с ${\ displaystyle n}$ непрерывной квадратичной функцией с ограничением, что ${\ displaystyle n}$ должно быть целым числом больше 1 при обращении к возможным состояниям кубов:

{\ displaystyle y = {\ textrm {A}} n ^ {2} + {\ textrm {B}} n + {\ textrm {C}}}

где A, B и C - константы. Константы A и B одинаковы для ${\ displaystyle n}$ даже и для ${\ displaystyle n}$ странно, но значение C другое.

Параметр	Стоимость
А	3,87785955497335
B	-3.61508538481188
C _ДАЖЕ	-1,71610938550614
C _ODD	-4,41947361312695
C _ЧЕТНЫЙ - C _{НЕЧЕТНЫЙ}	2,70336422762081

Графически, когда ${\ displaystyle y}$ строится, ^[24] две параболы точно такими же форм участвуют, с «даже» значениями кубы , лежащих на одной и «нечетные» значения кубы , лежащие на другом. Разница незаметна, за исключением случаев, когда график нанесен на небольшой диапазон ${\ displaystyle n}$ , как показано на приведенных ниже графиках. Только семейные ценности Рубика для ${\ displaystyle n}$ равные 2 и 3 включены во второй график.

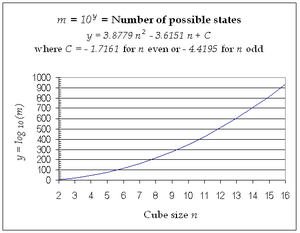Использование логарифмической функции y обеспечивает единственное практическое средство построения графиков чисел, которые варьируются в таком огромном диапазоне, как для семейства кубиков Рубика. Разница между кривыми составляет 505,08471690483 (что равно ${\ displaystyle {\ frac {{\ textrm {R}} ^ {0.5} {\ textrm {S}} ^ {0.25}} {\ textrm {Q}}}}$ ). Это фактор, который определяет влияние четного размера по сравнению с нечетным размером на количество достижимых состояний для кубов с немаркированными центрами.

Следовательно, при логарифмическом представлении количество состояний куба может быть выражено с помощью всего четырех ^[27] чисел (A, B и два значения C). Кроме того, количество состояний куба формирует ограниченный набор значений для более общей непрерывной квадратичной (параболической) функции, для которой ${\ displaystyle n}$ могут иметь нецелые и отрицательные значения. Вычисление значения m из соответствующего значения y - простой процесс.

Центральные кубы отличаются от угловых или краевых кубов тем, что, если они не имеют ориентировочной маркировки, есть несколько возможностей для их окончательной ориентации и / или местоположения. Может представлять интерес количество различных способов расположения центральных кубов для получения решенного куба с немаркированными центральными кубами. Чтобы рассчитать это, необходимо оценить влияние разметки центрального куба. Определять ${\ displaystyle m _ {\ textrm {M}}}$ , ${\ displaystyle {\ textrm {Q}} _ {\ textrm {M}}}$ , и ${\ displaystyle {\ textrm {S}} _ {\ textrm {M}}}$ быть измененными параметрами для отмеченных центральных кубов (P и R остаются без изменений).

{\ displaystyle {\ textrm {Q}} _ {\ textrm {M}} = {\ textrm {TQ}}}

куда

{\ displaystyle {\ textrm {T}} = {\ frac {4 ^ {6}} {2}} = 2048}

{\ displaystyle {\ textrm {S}} _ {\ textrm {M}} = {\ textrm {VS}}}

куда

{\ displaystyle {\ textrm {V}} = {\ frac {(4!) ^ {6}} {2}} = 95551488}

{\ displaystyle m _ {\ textrm {M}} = {\ textrm {P}} \ left ({\ textrm {Q}} _ {\ textrm {M}} \ right) ^ {a} {\ textrm {R} } ^ {b} \ left ({\ textrm {S}} _ {\ textrm {M}} \ right) ^ {c}}

{\ displaystyle m _ {\ textrm {M}} = m _ {\ textrm {D}} m}

{\ displaystyle m _ {\ textrm {M}} = {\ textrm {T}} ^ {a} {\ textrm {V}} ^ {c}}

Параметр ${\ displaystyle m _ {\ textrm {M}}}$ определяет количество достижимых состояний для кубов с отмеченными центрами. Фактор ${\ displaystyle m _ {\ textrm {D}}}$ дает количество различных расположений немаркированных центральных кубов, которые обеспечат решенный размер ${\ displaystyle n}$ куб. Это также коэффициент, на который нужно умножить количество различных состояний для стандартного куба, когда применяются отмеченные центры.

Недостижимые состояния для кубов всех размеров

Количество недостижимых состояний намного превышает количество достижимых состояний. Есть много ссылок на количество недостижимых состояний для куба размера 3, но очень мало для кубов большего размера.

Недостижимое расположение угловых и краевых кубов одинаково для кубов с отмеченным центром или без него.

Если рассматривать угловой куб для кубиков любого размера, то поворот на 1/3 по часовой стрелке, оставляющий все остальное без изменений, будет представлять недостижимое состояние, и аналогично для поворота на 1/3 против часовой стрелки. Следовательно, достижима только 1/3 возможностей скручивания.

Для куба с центральным краем для кубов нечетного размера поведение такое же, как и для куба размера 3. Достижима только половина возможных позиций и только половина возможных ориентаций. Следовательно, доступна только 1/4 возможностей перемещения куба по центру.

Реберные кубы, состоящие из 12 дополнительных пар (всего 24 куба), ведут себя так, как если бы дополнительные кубы не выглядели одинаково. Любой заданный крайний кубик может перемещаться в любую позицию на 24-кубовой орбите, но для любой заданной позиции существует одна достижимая и одна недостижимая ориентация для этого куба. Обратное применимо к дополнительному краевому кубу. Для данного куба (1-2) достижимая и недостижимая ориентации для данной грани для данной орбиты для куба размера 8 показаны ниже. Одна из 24 достижимых возможностей для данного граничного куба соответствует таковой для заданного куба.

Количество недостижимых состояний для набора с 24 гранями равно количеству достижимых состояний (24! В каждом случае).

В случае отмеченных центральных кубов достижима только половина возможных конфигураций для каждого набора из 24 кубов для любой заданной орбиты. ^[2] Те же правила четности, которые применяются к помеченным центральным кубам, также применяются к немаркированным центральным кубам. Четверть оборота набора из четырех центральных кубов не может быть достигнута без изменения компоновки в другом месте для соответствия требованию четности. Поскольку существует 95551488 способов упорядочения отдельных центральных кубов так, чтобы результирующее расположение выглядело точно таким же, правила четности могут выполняться без каких-либо наблюдаемых указаний на то, как достигается соответствие четности. Следовательно, для нормального случая (24 куба, содержащих по четыре цвета каждого из шести цветов) нет ограничений на достижимые состояния для центральных кубов.

В следующей таблице используются значения, указанные выше, для представления коэффициентов компонента k для размера. ${\ displaystyle n}$ куб. Показатели a , b и c являются функциями размера куба ${\ displaystyle n}$ как определено выше.

Компоненты приведения для коэффициента k (для стандартного куба с немаркированными центрами) и для ${\ Displaystyle к _ {\ textrm {M}}}$ (для куба с отмеченными центрами)	Тип куба немаркированных центров	Тип куба с выделенными центрами
Угловой кубический фактор	3	3
Фактор куба центрального ребра (такие кубы существуют только для кубов нечетного размера)	${\ displaystyle 2 ^ {2a}}$	${\ displaystyle 2 ^ {2a}}$
Дополнительный крайний кубический фактор для всех 12-парных комплектов вместе взятых	${\ displaystyle 2 ^ {b}}$	${\ displaystyle 2 ^ {b}}$
Абсолютный коэффициент центрального куба (такие кубы существуют только для кубов нечетного размера)	1	${\ Displaystyle 2 ^ {а}}$
Фактор центрального куба для всех комплектов на 24 куба вместе	1	${\ displaystyle 2 ^ {c}}$

Взяв продукт этих факторов:

Для стандартного размера ${\ displaystyle n}$ куб	${\ Displaystyle к = \ влево (3 \ вправо) 2 ^ {2a + b}}$
На размер отмеченных центров ${\ displaystyle n}$ куб	${\ Displaystyle к _ {\ textrm {M}} = \ влево (3 \ вправо) 2 ^ {3a + b + c}}$

Ниже приведены некоторые значения для кубиков небольшого размера.

Размер куба	2	3	4	5	6	7	8
Значение ${\ displaystyle k}$	3	12	6	24	12	48	24
Значение ${\ Displaystyle к _ {\ textrm {M}}}$	3	24	12	192	192	6144	12288

Количество недостижимых состояний определяется выражением ${\ Displaystyle (к-1) м}$ для стандартных кубиков и по ${\ displaystyle (к _ {\ textrm {M}} - 1) m _ {\ textrm {M}}}$ для кубиков с отмеченными центральными кубиками.

Примечания и ссылки

^ https://speedcubeshop.com/products/shengshou-19x19
^ a b c d e Кен Фрейзер, «Реализация и решение кубиков семейства Рубика с помеченными центрами» . Проверено 24 февраля 2017.
^ a b Райан Хейз, "Теория кубика Рубика - Законы куба". Архивировано 2 августа 2013 г. в Wayback Machine . Проверено 24 февраля 2017.
^ a b Арфур Догфри, "Школа математики для собак: 12. Волшебный кубик Рубика" . Проверено 24 февраля 2017.
^ a b c d Кен Фрейзер, "Правила для кубиков семьи Рубика всех размеров" . Проверено 24 февраля 2017.
^ a b Том Дэвис, "Теория групп через кубик Рубика" . Проверено 24 февраля 2017.
^ a b Том Дэвис, «Математика кубика Рубика» . Проверено 24 февраля 2017.
^ Арфур Догфри, "Школа математики для собак: Введение в теорию групп" . Проверено 24 февраля 2017.
^ Райан Хейз, "Теория кубика Рубика - паритет" . Проверено 24 февраля 2017.
^ a b c Кен Фрейзер, «Распутывание кубиков размером 2x2x2 и выше» . Проверено 24 февраля 2017.
↑ Питер Стилл, «Решение для начинающих кубика Рубика» . Проверено 24 февраля 2017.
^ Puzzle Яап Страница, «Месть Рубика (решение)» . Проверено 24 февраля 2017.
^ Крис Хардвик, «Решение мести Рубика (4x4x4)» . Проверено 24 февраля 2017.
^ Роберт Мунафо, "Инструкции по решению кубиков размера 2, 3, 4 и 5" . Проверено 24 февраля 2017.
^ a b Кен Фрейзер, "Инструкции по сборке кубиков разного размера" . Проверено 24 февраля 2017.
^ Мэтью Монро, «Как обрабатывать изображения или логотипы на лицах» . Проверено 24 февраля 2017.
↑ Эрик Дитц (умерший), «Решатель куба Рубика» . Проверено 24 февраля 2017.
^ Крис Хардвик, «Исправить четность для куба 4x4x4» . Проверено 24 февраля 2017.
↑ Том Дэвис, «Пробный выпуск Рубика» . Проверено 24 февраля 2017.
^ Томас Rokicki, Герберт Kociemba, Морли Дэвидсон и Джон Dethridge, «Номер Божье 20» . Проверено 24 февраля 2017.
^ a b Оливер Мейсон, «Некоторые простые правила подсчета, EE304 - Вероятность и статистика» . Проверено 24 февраля 2017.
^ Хофштадтер, DR, Metamagical Themas, "cubies волшебный кубик в вертел от кубистов и решается cubemeisters", Scientific American, март 1981.
^ Puzzle Яапа Страница, «Перестановка и недостижимые состояния для размера 3x3x3 куба» Архивированных 2013-07-28 в Wayback Machine . Проверено 24 февраля 2017.
^ a b c d e Кен Фрейзер, "Кубик Рубика расширенный: определение числа состояний для кубов любого размера и значений до размера 25x25x25" . Проверено 24 февраля 2017.
^ Ричард Карр, "Число возможных положений N x N x N кубика Рубика" . Проверено 24 февраля 2017.
^ Крис Хардвик, «Количество комбинаций кубика Рубика и вариаций» . Проверено 24 февраля 2017.
^ Математическая справка, «нецелое число» . Проверено 24 февраля 2017.

[a-10] Поскольку ${\ Displaystyle \ влево (п-2 \ вправо) ^ {2} -1}$ равно ${\ Displaystyle \ влево (п-1 \ вправо) \ влево (п-3 \ вправо)}$ , произведение двух последовательных четных чисел, которые всегда должны делиться на 8 без остатка.

[b-11] Поскольку ${\ displaystyle \ left ({\ frac {n} {2}} - 1 \ right) ^ {2}}$ будет странно, если ${\ displaystyle \ left ({\ frac {n} {2}} - 1 \ right)}$ нечетное (т.е. если ${\ displaystyle {\ frac {n} {2}}}$ является четным), что дает в целом даже с тех пор, как ${\ Displaystyle (п-1)}$ странно. Обратное верно, если ${\ displaystyle {\ frac {n} {2}}}$ странно.

[1] ttps://speedcubeshop.com/products/shengshou-19x19

[fraser_marked-2] Кен Фрейзер, «Реализация и решение кубиков семейства Рубика с помеченными центрами» . Проверено 24 февраля 2017.

[heise_laws-3] Райан Хейз, "Теория кубика Рубика - Законы куба". Архивировано 2 августа 2013 г. в Wayback Machine . Проверено 24 февраля 2017.

[dogfrey_magic_cube-4] Арфур Догфри, "Школа математики для собак: 12. Волшебный кубик Рубика" . Проверено 24 февраля 2017.

[fraser_rules-5] Кен Фрейзер, "Правила для кубиков семьи Рубика всех размеров" . Проверено 24 февраля 2017.

[davis_permut-6] Том Дэвис, "Теория групп через кубик Рубика" . Проверено 24 февраля 2017.

[davis_gptheory-7] Том Дэвис, «Математика кубика Рубика» . Проверено 24 февраля 2017.

[8] Арфур Догфри, "Школа математики для собак: Введение в теорию групп" . Проверено 24 февраля 2017.

[9] Райан Хейз, "Теория кубика Рубика - паритет" . Проверено 24 февраля 2017.

[fraser_unravel-12] Кен Фрейзер, «Распутывание кубиков размером 2x2x2 и выше» . Проверено 24 февраля 2017.

[13] Питер Стилл, «Решение для начинающих кубика Рубика» . Проверено 24 февраля 2017.

[14] Puzzle Яап Страница, «Месть Рубика (решение)» . Проверено 24 февраля 2017.

[15] Крис Хардвик, «Решение мести Рубика (4x4x4)» . Проверено 24 февраля 2017.

[16] Роберт Мунафо, "Инструкции по решению кубиков размера 2, 3, 4 и 5" . Проверено 24 февраля 2017.

[fraser_solving_unmarked-17] Кен Фрейзер, "Инструкции по сборке кубиков разного размера" . Проверено 24 февраля 2017.

[18] Мэтью Монро, «Как обрабатывать изображения или логотипы на лицах» . Проверено 24 февраля 2017.

[19] Эрик Дитц (умерший), «Решатель куба Рубика» . Проверено 24 февраля 2017.

[20] Крис Хардвик, «Исправить четность для куба 4x4x4» . Проверено 24 февраля 2017.

[21] Том Дэвис, «Пробный выпуск Рубика» . Проверено 24 февраля 2017.

[22] Томас Rokicki, Герберт Kociemba, Морли Дэвидсон и Джон Dethridge, «Номер Божье 20» . Проверено 24 февраля 2017.

[mason-23] Оливер Мейсон, «Некоторые простые правила подсчета, EE304 - Вероятность и статистика» . Проверено 24 февраля 2017.

[24] Хофштадтер, DR, Metamagical Themas, "cubies волшебный кубик в вертел от кубистов и решается cubemeisters", Scientific American, март 1981.

[25] Puzzle Яапа Страница, «Перестановка и недостижимые состояния для размера 3x3x3 куба» Архивированных 2013-07-28 в Wayback Machine . Проверено 24 февраля 2017.

[fraser_states-26] Кен Фрейзер, "Кубик Рубика расширенный: определение числа состояний для кубов любого размера и значений до размера 25x25x25" . Проверено 24 февраля 2017.

[27] Ричард Карр, "Число возможных положений N x N x N кубика Рубика" . Проверено 24 февраля 2017.

[28] Крис Хардвик, «Количество комбинаций кубика Рубика и вариаций» . Проверено 24 февраля 2017.

[29] Математическая справка, «нецелое число» . Проверено 24 февраля 2017.

[1]