В информатике слияние - это свойство переписывания систем, описывающее, какие термины в такой системе можно переписать более чем одним способом, чтобы получить тот же результат. В этой статье описываются свойства в наиболее абстрактной обстановке абстрактной системы перезаписи .
Мотивирующие примеры [ править ]
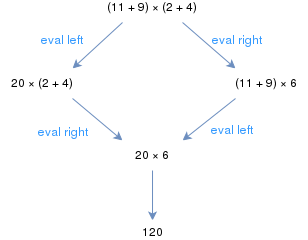
Обычные правила элементарной арифметики образуют абстрактную систему переписывания. Например, выражение (11 + 9) × (2 + 4) может быть вычислено, начиная с левой или с правой круглой скобки; однако в обоих случаях в конечном итоге получается один и тот же результат. Это говорит о том, что система арифметического переписывания является единой.
Второй, более абстрактный пример получается из следующего доказательства того, что каждый элемент группы равен обратному своему обратному: [1]
| A1 | 1 ⋅ а | = а |
| A2 | а −1 ⋅ а | = 1 |
| A3 | ( а ⋅ б ) ⋅ с | = a ⋅ ( b ⋅ c ) |
| а −1 ⋅ ( а ⋅ б ) | ||
| знак равно | ( a −1 ⋅ a ) ⋅ b | по A3 (r) |
| знак равно | 1 ⋅ б | автор: A2 |
| знак равно | б | автор: A1 |
| ( а −1 ) −1 ⋅ 1 | ||
| знак равно | ( a −1 ) −1 ⋅ ( a −1 ⋅ a ) | по A2 (r) |
| знак равно | а | по R4 |
| ( a −1 ) −1 ⋅ b | ||
| знак равно | ( a −1 ) −1 ⋅ ( a −1 ⋅ ( a ⋅ b )) | по R4 (r) |
| знак равно | а ⋅ б | по R4 |
| а ⋅ 1 | ||
| знак равно | ( а −1 ) −1 ⋅ 1 | по R10 (r) |
| знак равно | а | по R6 |
| ( а −1 ) −1 | ||
| знак равно | ( а −1 ) −1 ⋅ 1 | по R11 (r) |
| знак равно | а | по R6 |
Это доказательство начинается с данных групповых аксиом A1-A3 и устанавливает пять утверждений R4, R6, R10, R11 и R12, каждое из которых использует некоторые более ранние, а R12 является основной теоремой. Некоторые доказательства требуют неочевидных, если не творческих, шагов, таких как применение аксиомы A2 в обратном порядке, тем самым переписывая «1» на « a −1 ⋅ a» на первом этапе доказательства R6. Одним из исторических мотивов разработки теории переписывания терминов было стремление избежать необходимости в таких шагах, которые трудно найти неопытному человеку, не говоря уже о компьютерной программе.
Если термин системы переписывания является сливающимся и терминатором , простой метод существует , чтобы доказать равенство между двумя выражениями (акой точки ) s и т : Начиная с й , применяется равенства [примечание 1] слева направо как можно дольше, в конечном итоге получения термин s ' . Получите из t член t ' аналогичным образом. Если оба условия s и t буквально совпадают, то s и t (что неудивительно) оказываются равными. Более важно, если они не согласны, sи t не может быть равным. То есть любые два члена s и t, которые вообще могут быть доказаны равными, могут быть таковыми с помощью этого метода.
Успех этого метода не зависит от определенного сложного порядка применения правил перезаписи, поскольку слияние гарантирует, что любая последовательность применения правил в конечном итоге приведет к одному и тому же результату (в то время как свойство завершения гарантирует, что любая последовательность в конечном итоге достигнет конца вообще). Следовательно, если для некоторой эквациональной теории может быть предусмотрена сливающаяся и завершающая система переписывания терминов, [примечание 2] не требуется ни малейшего творчества для выполнения доказательств равенства терминов; эта задача, следовательно, становится доступной для компьютерных программ. Современные подходы обрабатывать более общие абстрактные системы переписывания , а не термин переписывания системы; последние являются частным случаем первого.
Общий случай и теория [ править ]
Система перезаписи может быть выражена как ориентированный граф, в котором узлы представляют выражения, а ребра представляют перезаписи. Так, например, если выражение можно переписать в Ь , то мы говорим , что б является редуктом из ( в качестве альтернативы, сводится к Ь , или является расширением из б ). Это представлено стрелками; a → b указывает, что a сводится к b . Интуитивно, это означает , что соответствующий граф имеет направленное ребро из а к б .
Если есть путь между двумя узлами графа c и d , то он образует редукционную последовательность . Так, например, если c → c ' → c' → ... → d → d , то мы можем написать c d , что указывает на существование редукционной последовательности от c до d . Формально,является рефлексивно-транзитивным замыканием →. Используя пример из предыдущего абзаца, мы имеем (11 + 9) × (2 + 4) → 20 × (2 + 4) и 20 × (2 + 4) → 20 × 6, поэтому (11 + 9) × ( 2 + 4) 20 × 6.
Установив это, слияние можно определить следующим образом. a ∈ S считается конфлюэнтным, если для всех пар b , c ∈ S таких, что a б и а с , существует d ∈ S с б d и c d . Если каждый a ∈ S конфлюэнтен, мы говорим, что → конфлюэнтен или обладает свойством Черча-Россера . Это свойство также иногда называют свойством ромба по форме диаграммы, показанной справа. Некоторые авторы оставляют за собой термин « алмазное свойство» для варианта диаграммы с единичными редукциями повсюду; то есть всякий раз, когда a → b и a → c , должно существовать d такое, что b → d и c → d. Вариант с одним редуктором строго сильнее, чем вариант с несколькими редукторами.
Местное слияние [ править ]


Элемент a ∈ S называется локально (или слабо) конфлюэнтным, если для всех b , c ∈ S с a → b и a → c существует d ∈ S с b d и c d . Если каждый элемент a ∈ S локально конфлюэнтен, то → называется локально (или слабо) конфлюэнтным или обладает слабым свойством Черча-Россера . Это отличается от слияния тем, что b и c должны быть уменьшены с a за один шаг. По аналогии с этим слияние иногда называют глобальным слиянием .
Соотношение , Вводятся в качестве обозначения для последовательностей сокращения, может рассматриваться как переписывания системы в своем собственном праве, чье соотношение является рефлексивным-транзитивным замыканием на → . Поскольку последовательность редукционных последовательностей снова является редукционной последовательностью (или, что то же самое, поскольку формирование рефлексивно-транзитивного замыкания идемпотентно ), знак равно . Отсюда следует, что → конфлюэнтно тогда и только тогда, когда локально сливается.
Система перезаписи может быть локально конфлюэнтной, но не (глобальной) конфлюэнтной. Примеры показаны на рисунках 3 и 4. Однако лемма Ньюмана утверждает, что если локально конфлюэнтная система перезаписи не имеет бесконечных редукционных последовательностей (в этом случае она называется завершающей или строго нормализующей ), то она глобально конфлюэнтна.
Полуслияние [ править ]
Определение локального слияния отличается от определения глобального слияния тем, что учитываются только элементы, полученные из данного элемента за один шаг переписывания. Рассматривая один элемент, достигаемый за один шаг, и другой элемент, достигаемый произвольной последовательностью, мы приходим к промежуточному понятию полуслияния: элемент a ∈ S называется полуслитым, если для всех b , c ∈ S с a → б и а с существует d ∈ S с б d и c d ; если каждый a ∈ S полуконфлюэнтен, мы говорим, что → полуконфлюэнтно.
Полуконфлюэнтный элемент не обязательно должен быть конфлюэнтным, но полуконфлюэнтная система перезаписи обязательно конфлюэнтна, а конфлюэнтная система тривиально полуконфлюэнтна.
Сильное слияние [ править ]
Сильное слияние - это еще один вариант локального слияния, позволяющий сделать вывод о глобальном слиянии системы переписывания. Элемент a ∈ S называется сильно конфлюэнтным, если для всех b , c ∈ S с a → b и a → c существует d ∈ S с b d и либо c → d, либо c = d ; если каждый a ∈ S сильно конфлюэнтен, мы говорим, что → сильно конфлюэнтно.
Конфлюэнтный элемент не обязательно должен быть сильно конфлюэнтным, но сильно конфлюэнтная система переписывания обязательно конфлюэнтна.
Примеры конфлюэнтных систем [ править ]
- Редукция полиномов по модулю идеала - это конфлюэнтная система перезаписи при условии, что она работает с базисом Грёбнера .
- Теорема Мацумото следует из слияния соотношений кос.
- β-редукция λ-членов сливается по теореме Черча-Россера .
См. Также [ править ]
- Сходимость (логика)
- Критическая пара (логика)
- Нормальная форма (реферат)
Заметки [ править ]
- ^ затем вызвал правила перезаписи, чтобы подчеркнуть их ориентацию слева направо
- ^ Алгоритм завершения Кнута-Bendix можно использовать для вычисления такой системы из заданного набора уравнений. Такая система, например, для групп, показана здесь с последовательной нумерацией ее предложений. Используя его, доказательство, например, R6 состоит в применении R11 и R12 в любом порядке к ( a −1 ) −1 ⋅1, чтобы получить a .; никакие другие правила не применяются.
Ссылки [ править ]
- Системы перезаписи терминов , Тереза, Кембриджский трактат по теоретической информатике, 2003.
- Изменение терминов и все такое , Франц Баадер и Тобиас Нипков , Cambridge University Press, 1998 г.
- ^ KH Власий и Х.-Ю. Bürckert, ed. (1992). Deduktionsssysteme . Ольденбург. п. 291.; здесь: с.134; Названия аксиом и предложений следуют за исходным текстом
- ^ a b Н. Дершовиц, Ж.-П. Жуанно (1990). «Системы перезаписи». В Яне ван Леувене (ред.). Формальные модели и семантика . Справочник по теоретической информатике. B . Эльзевир. С. 243–320. ISBN 0-444-88074-7. Здесь: стр.268, рис. 2а + б.
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Сливающийся» . MathWorld .