Эта статья включает в себя список литературы , связанной литературы или внешних ссылок , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( Октябрь 2015 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения ) |
| Связать / вырезать дерево | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тип | Дерево | |||||||||||||||
| Изобретенный | 1982 г. | |||||||||||||||
| Изобретенный | ||||||||||||||||
| Сложность времени в большой нотации O | ||||||||||||||||
| ||||||||||||||||
Ссылка / вырезать дерево представляет собой структуру данных для представления леса , набор корневых деревьев , и предлагает следующие операции:
- Добавьте в лес дерево, состоящее из одного узла.
- Для данного узла в одном из деревьев отсоедините его (и его поддерево) от дерева, частью которого он является.
- Присоедините узел к другому узлу в качестве его дочернего элемента.
- Для данного узла найдите корень дерева, которому он принадлежит. Выполняя эту операцию на двух разных узлах, можно проверить, принадлежат ли они к одному дереву.
Представленный лес может состоять из очень глубоких деревьев, поэтому, если мы представим лес как простую коллекцию родительских деревьев указателей , нам может потребоваться много времени, чтобы найти корень данного узла. Однако, если мы представим каждое дерево в лесу как дерево связей / разрезов, мы сможем найти, к какому дереву принадлежит элемент, за O (log ( n )) амортизированного времени. Более того, мы можем быстро настроить набор деревьев ссылок / разрезов в соответствии с изменениями в представленном лесу. В частности, мы можем настроить его для объединения (связывания) и разделения (вырезания) за O ( log (n)) амортизированного времени.
Деревья связей / разрезов разделяют каждое дерево в представленном лесу на пути, не пересекающиеся с вершинами, где каждый путь представлен вспомогательной структурой данных (часто расширяемыми деревьями , хотя исходная статья предшествует расширенным деревьям и, таким образом, использует смещенные деревья двоичного поиска). Узлы во вспомогательной структуре данных упорядочены по их глубине в соответствующем представленном дереве. В одном из вариантов, Naive Partitioning , пути определяются последними доступными путями и узлами, как и в Tango Trees . При разбиении по размерупути определяются самым тяжелым дочерним элементом (дочерним элементом с наибольшим количеством детей) данного узла. Это дает более сложную структуру, но снижает стоимость операций с амортизированного O (log n) до наихудшего случая O (log n). Он используется для решения множества проблем с сетевым потоком и для объединения наборов данных.
В оригинальной публикации Слеатор и Тарьян называли деревья ссылок / разрезов «динамическими деревьями» или «динамическими динамометрическими деревьями».
Структура [ править ]
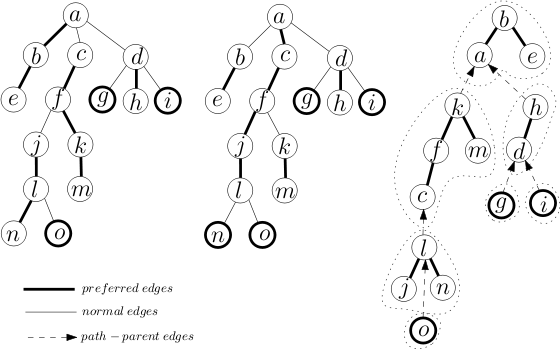
Мы берем дерево, в котором каждый узел имеет произвольную степень неупорядоченности узлов, и разбиваем его на пути. Мы называем это изображенным деревом . Эти пути представлены внутри вспомогательными деревьями (здесь мы будем использовать расширенные деревья), где узлы слева направо представляют путь от корня до последнего узла на пути. Узлы, которые связаны в представленном дереве, которые не находятся на одном предпочтительном пути (и, следовательно, не в одном вспомогательном дереве), соединяются через указатель на родительский путь . Этот указатель хранится в корне вспомогательного дерева, представляющего путь.
Предпочтительные пути [ править ]
Когда в представленном дереве осуществляется доступ к узлу v , выбранный путь становится предпочтительным . Предпочтительный ребенок узла является последним ребенком , который был на пути доступа, или нуль , если последний доступ был к V или если не доступы сделано не было этой конкретной ветви дерева. Предпочтительный край является краем , который соединяет предпочтительную ребенка к V .
В альтернативной версии предпочтительные пути определяются самым тяжелым дочерним элементом.
Операции [ править ]
Нас интересуют операции FindRoot (Node v), Cut (Node v), Link (Node v, Node w) и Path (Node v). Каждая операция выполняется с помощью подпрограммы Access (Node v). Когда мы обращаемся к вершине v , предпочтительный путь представленного дерева изменяется на путь от корня R представленного дерева к узлу v . Если узел на пути доступа ранее имел предпочтительный дочерний элемент u , а теперь путь идет к дочернему элементу w , старое предпочтительное ребро удаляется (заменяется указателем на родительский путь ), и новый путь теперь проходит через w .
Доступ [ редактировать ]
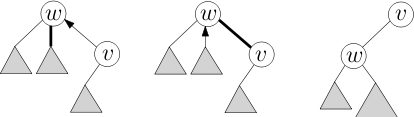
После выполнения доступа к узлу v у него больше не будет предпочтительных дочерних узлов и он будет в конце пути. Поскольку узлы вспомогательного дерева имеют ключ по глубине, это означает, что любые узлы справа от v вспомогательного дерева должны быть отключены. В растянутом дереве это относительно простая процедура; мы расширяем v , что приводит v к корню вспомогательного дерева. Затем мы отключаем правое поддерево v , то есть каждый узел, который находился ниже него по предыдущему предпочтительному пути. У корня отключенного дерева будет указатель на родительский путь, который мы указываем на v .
Теперь мы поднимаемся по представленному дереву к корню R , ломая и сбрасывая предпочтительный путь там, где это необходимо. Для этого мы следуем за указателем-родительским путем от v (поскольку v теперь является корнем, у нас есть прямой доступ к указателю-родительскому пути). Если путь, на котором находится v, уже содержит корень R (поскольку узлы имеют ключ по глубине, это будет крайний левый узел во вспомогательном дереве), указатель на родительский путь будет нулевым, и мы закончим доступ. В противном случае мы следуем по указателю на некоторый узел на другом пути w . Мы хотим сломать старый предпочтительный путь w и повторно подключить его к пути v . Для этого раскладываем на w, и отсоедините его правое поддерево, установив для его родительского указателя пути значение w . Поскольку все узлы имеют ключ по глубине, и каждый узел на пути v глубже, чем каждый узел на пути w (поскольку они являются потомками w в представленном дереве), мы просто подключаем дерево v как правый дочерний элемент. из w . Мы снова расширяем точку v , которая, поскольку v является потомком корня w , просто превращает v в корень. Мы повторяем весь этот процесс до тех пор, пока родительский указатель пути для v не станет нулевым, после чего он окажется на том же предпочтительном пути, что и корень представленного дерева R.
FindRoot [ править ]
FindRoot относится к поиску корня представленного дерева, содержащего узел v . Поскольку подпрограмма доступа помещает v в предпочтительный путь, мы сначала выполняем доступ. Теперь узел v находится на том же самом предпочтительном пути, и , таким образом тот же вспомогательный дерева в качестве корневого R . Поскольку вспомогательные деревья имеют ключ по глубине, корень R будет крайним левым узлом вспомогательного дерева. Таким образом , мы просто выбираем левую ребенка V рекурсивно , пока мы не можем идти дальше, и этот узел является корнем R . Корень может быть линейно глубоким (что наихудший случай для расширенного дерева), поэтому мы расширяем его так, чтобы следующий доступ был быстрым.
Вырезать [ править ]
Здесь мы хотим разрезать представленное дерево в узле v . Сначала мы обращаемся к v . Это помещает все элементы ниже v в представленное дерево как правые дочерние элементы v во вспомогательном дереве. Все элементы, которые теперь находятся в левом поддереве v, являются узлами выше, чем v в представленном дереве. Поэтому мы отключаем левый дочерний элемент v (который по-прежнему поддерживает привязку к исходному представленному дереву через указатель на родительский путь). Теперь v - корень представленного дерева. Доступ к v также прерывает предпочтительный путь ниже v , но это поддерево поддерживает соединение сv через указатель на родительский путь.
Ссылка [ редактировать ]
Если v - корень дерева, а w - вершина в другом дереве, соедините деревья, содержащие v и w , добавив ребро (v, w), сделав w родителем v . Для этого мы обращаемся к v и w в их соответствующих деревьях и делаем w левым потомком v . Поскольку v является корнем, а узлы привязаны к глубине во вспомогательном дереве, доступ к v означает, что v не будет иметь левого дочернего элемента во вспомогательном дереве (поскольку в качестве корня это минимальная глубина). Добавление w в качестве левого дочернего элемента фактически делает его родительским элементомv в изображенном дереве.
Путь [ править ]
Для этой операции мы хотим выполнить некоторую агрегатную функцию по всем узлам (или ребрам) на пути от корня R до узла v (например, «сумма», «мин», «макс.» Или «увеличение» и т. Д.). Для этого мы обращаемся к v , что дает нам вспомогательное дерево со всеми узлами на пути от корня R до узла v . Структура данных может быть дополнена данными, которые мы хотим получить, такими как минимальные или максимальные значения или сумма затрат в поддереве, которые затем могут быть возвращены по заданному пути в постоянное время.
Псевдокод операций [ править ]
Переключить-предпочтительный-дочерний (x, y): путь-родитель (right (x)) = x вправо (х, у)Доступ (v): Switch-Path-Parent (v, ноль) в то время как (v не является корнем) w = родительский путь (v) растянуть (ш) Switch-Path-Parent (ш, в) путь-родитель (v) = нуль v = w растянуть (v)Ссылка (v, w): Доступ (v) Доступ (w) left (v) = wВырезать (v): Доступ (v) left (v) = нольАнализ [ править ]
Вырезать и связать стоит O (1) плюс стоимость доступа. FindRoot имеет амортизированную верхнюю границу O (log n ) плюс стоимость доступа. Структура данных может быть дополнена дополнительной информацией (например, минимальным или максимальным значением узла в его поддеревьях или суммой), в зависимости от реализации. Таким образом, Path может возвращать эту информацию за постоянное время плюс границу доступа.
Так что осталось привязать доступ, чтобы узнать время нашей работы.
В Access используется расширение, которое, как мы знаем, имеет амортизированную верхнюю границу O (log n ). Итак, оставшийся анализ касается того, сколько раз нам нужно развернуться. Это равно количеству предпочтительных дочерних изменений (количеству ребер, измененных в предпочтительном пути), когда мы движемся вверх по дереву.
Мы ограничили доступ , используя технику под названием Heavy-Light Decomposition .
Разложение тяжелого-легкого [ править ]
Этот метод называет ребро тяжелым или легким в зависимости от количества узлов в поддереве. представляет количество узлов в поддереве v в представленном дереве. Ребро называется тяжелым , если размер (объем)> 1 / 2 размера (родитель (v)). Таким образом, мы видим, что у каждого узла может быть не более 1 тяжелого ребра. Кромка, которая не является тяжелой, называется легкой кромкой.
Под глубиной света понимается количество световых ребер на заданном пути от корня до вершины v . Light-depth ≤ lg n, потому что каждый раз, когда мы пересекаем светлое ребро, мы уменьшаем количество узлов как минимум в 2 раза (поскольку он может иметь не более половины узлов родительского элемента).
Таким образом, данное ребро в представленном дереве может быть любым из четырех возможных: сильное предпочтение , тяжелое нежелание , легкое предпочтение или легкое нежелательное .
Сначала докажем оценку сверху.
O (log 2 n ) верхняя граница [ править ]
Операция расширения доступа дает нам log n , поэтому нам нужно ограничить количество обращений до log n, чтобы доказать верхнюю границу O (log 2 n ).
Каждое изменение предпочтительной кромки приводит к формированию новой предпочтительной кромки. Итак, мы подсчитываем количество образованных предпочтительных ребер. Поскольку существует в большинстве лога п ребер, которые свет на любом заданном пути, есть лог - н легких краев к изменяющимся предпочтительным.
Количество тяжелых кромок, которые становятся предпочтительными, может быть для любой конкретной операции, но это амортизируется. За серию выполнений мы можем сделать n -1 тяжелых ребер предпочтительными (поскольку всего в представленном дереве не более n -1 тяжелых ребер), но с этого момента количество тяжелых ребер, которые становятся предпочтительными, равно количеству тяжелых кромок, которые стали нежелательными на предыдущем шаге. Для каждой тяжелой кромки, которая становится нежелательной, предпочтение должно отдаваться легкой кромке. Мы уже видели, что количество светлых ребер, которые могут стать предпочтительными, не превышает log n . Таким образом, количество тяжелых ребер, которые становятся предпочтительными для m операций, равно . При достаточном количестве операций ( ) в среднем.
Улучшение до O (log n ) верхней границы [ править ]
Мы связали количество предпочтительных дочерних изменений на , поэтому, если мы можем показать, что каждое предпочтительное дочернее изменение имеет амортизированную стоимость O (1), мы можем связать операцию доступа на . Это делается с помощью потенциального метода .
Пусть s (v) - количество узлов под v в дереве вспомогательных деревьев. Тогда потенциальная функция . Мы знаем, что амортизированная стоимость наращивания ограничена:
Мы знаем, что после раскрытия v является дочерним элементом своего родительского узла w . Итак, мы знаем, что:
Мы используем это неравенство и амортизированную стоимость доступа для получения телескопической суммы, которая ограничена:
где R - корень представленного дерева, и мы знаем количество предпочтительных дочерних изменений . s ( R ) = n , поэтому мы амортизировали.
Заявление [ править ]
Деревья связей / разрезов могут использоваться для решения проблемы динамической связности ациклических графов. Учитывая два узла x и y, они связаны тогда и только тогда, когда FindRoot (x) = FindRoot (y). Другая структура данных, которую можно использовать для той же цели, - дерево обхода Эйлера .
При решении задачи о максимальном потоке деревья ссылок / разрезов могут использоваться для улучшения времени работы алгоритма Диника с по .
См. Также [ править ]
- Splay tree
- Возможный метод
Дальнейшее чтение [ править ]
- Слеатор, ДД; Tarjan, RE (1983). «Структура данных для динамических деревьев». Материалы тринадцатого ежегодного симпозиума ACM по теории вычислений - STOC '81 (PDF) . п. 114. DOI : 10,1145 / 800076,802464 .
- Слеатор, ДД; Tarjan, RE (1985). «Самонастраивающиеся деревья двоичного поиска» (PDF) . Журнал ACM . 32 (3): 652. DOI : 10,1145 / 3828,3835 .
- Гольдберг, А.В .; Tarjan, RE (1989). «Нахождение минимальных тиражей за счет отмены отрицательных циклов». Журнал ACM . 36 (4): 873. DOI : 10,1145 / 76359,76368 . - Приложение к минимальному обороту
- Link-Cut деревья в: конспекты лекций по расширенным структурам данных, весна 2012 г., лекция 19. Проф. Эрик Демейн, Писцы: Писцы: Джастин Холмгрен (2012), Цзин Цзянь (2012), Максим Степаненко (2012), Mashhood Ishaque (2007 ).
- http://compgeom.cs.uiuc.edu/~jeffe/teaching/datastructures/2006/notes/07-linkcut.pdf