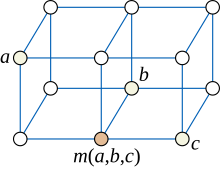
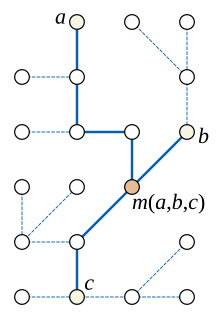
В теории графов , разделе математики , медианный граф - это неориентированный граф, в котором каждые три вершины a , b и c имеют уникальную медиану : вершину m ( a , b , c ), которая принадлежит кратчайшим путям между каждой парой. из a , b и c .
Концепция медианных графов уже давно изучается, например, Биркгофом и Киссом (1947) или (более явно) Аваном (1961) , но первая статья, в которой они названы «медианными графами», по-видимому, принадлежит Небески (1971) . Как пишут Чанг , Грэм и Сакс, «медианные графы возникают естественным образом при изучении упорядоченных множеств и дискретных дистрибутивных решеток , и по ним имеется обширная литература». [1] В филогенетике граф Бунемана, представляющий все эволюционные деревья максимальной экономии, является медианным графом. [2] Медианные графы также возникают в теории социального выбора.: если набор альтернатив имеет структуру медианного графа, можно однозначно вывести предпочтение большинства среди них. [3]
Дополнительные обзоры медианных графиков даны Klavžar & Mulder (1999) , Bandelt & Chepoi (2008) и Knuth (2008) .
Примеры [ править ]
Каждое дерево - это медианный граф. [4] Чтобы убедиться в этом, заметьте, что в дереве объединение трех кратчайших путей между парами трех вершин a , b и c является либо путем, либо поддеревом, образованным тремя путями, встречающимися в одном центре. узел с третьей степенью . Если объединение трех путей само является путем, медиана m ( a , b , c ) равна одному из a , b или c., в зависимости от того, какая из этих трех вершин находится между двумя другими на пути. Если поддерево, образованное объединением трех путей, не является путем, медиана трех вершин является центральным узлом третьей степени поддерева.
Дополнительные примеры медианных графов представлены сеточными графами . На сеточном графике координаты медианы m ( a , b , c ) могут быть найдены как медиана координат точек a , b и c . Наоборот, оказывается, что в каждом медианном графе можно пометить вершины точками в целочисленной решетке таким образом, чтобы медианы могли быть вычислены таким образом покоординатно. [5]
Квадратные графы, плоские графы, в которых все внутренние грани являются четырехугольниками, а все внутренние вершины имеют четыре или более инцидентных ребра, являются еще одним подклассом медианных графов. [6] Полимин является частным случаем рамочного графа и , следовательно , также образует средний график. [7]
Симплекс график κ ( G ) произвольного неориентированного графа G имеет вершину для каждого клика (полный подграф) из G ; два вершина х ( G ) связаны ребром , если соответствующие клики отличаются одной вершиной из G . Симплексный граф всегда является медианным графом, в котором медиана данной тройки клик может быть сформирована с использованием правила большинства, чтобы определить, какие вершины клик нужно включить. [8]
Нет цикла график длины, кроме четырех может быть средний график. Каждый такой цикл имеет три вершины a , b и c , так что три кратчайших пути охватывают весь цикл без общего пересечения. Для такой тройки вершин не может быть медианы.
Эквивалентные определения [ править ]
В произвольном графе для каждых двух вершин a и b минимальное количество ребер между ними называется их расстоянием и обозначается d ( x , y ). Интервал вершин , которые лежат на кратчайших между и б определяется как
- I ( a , b ) = { v | d ( a , b ) = d (a, v) + d (v, b) }.
Медианный граф определяется тем свойством, что для каждых трех вершин a , b и c эти интервалы пересекаются в одной точке:
- Для всех a , b и c | I ( a , b ) ∩ I ( a , c ) ∩ I ( b , c ) | = 1.
Эквивалентно, для каждых трех вершин a , b и c можно найти вершину m ( a , b , c ) такую, что невзвешенные расстояния в графе удовлетворяют равенствам
- d ( a , b ) = d ( a , m ( a , b , c )) + d ( m ( a , b , c ), b )
- d ( a , c ) = d ( a , m ( a , b , c )) + d ( m ( a , b , c ), c )
- d ( b , c ) = d ( b , m ( a , b , c )) + d ( m ( a , b , c ), c )
и m ( a , b , c ) - единственная вершина, для которой это верно.
Также возможно определить медианные графы как наборы решений задач 2-выполнимости , как ретракты гиперкубов , как графы конечных медианных алгебр , как графы Бунемана расщепленных систем Хелли и как графы Windex 2; см. разделы ниже.
Дистрибутивные решетки и медианные алгебры [ править ]
В теории решетки граф конечной решетки имеет вершину для каждого элемента решетки и ребро для каждой пары элементов в отношении покрытия решетки. Решетки обычно представляются визуально с помощью диаграмм Хассе , которые представляют собой рисунки графов решеток. Эти графы, особенно в случае дистрибутивных решеток , оказываются тесно связанными с медианными графами.
В дистрибутивной решетке самодуальная тернарная медианная операция Биркгофа [9]
- m ( a , b , c ) = ( a ∧ b ) ∨ ( a ∧ c ) ∨ ( b ∧ c ) = ( a ∨ b ) ∧ ( a ∨ c ) ∧ ( b ∨ c ),
удовлетворяет определенным ключевым аксиомам, которые он разделяет с обычной медианой чисел в диапазоне от 0 до 1 и с медианными алгебрами в целом:
- Идемпотентность : m (a, a, b) = a для всех a и b .
- Коммутативность : m ( a , b , c ) = m (a, c, b) = m (b, a, c) = m (b, c, a) = m (c, a, b) = m (c , b, a) для всех a , b и c .
- Дистрибутивность : m (a, m (b, c, d), e) = m (m (a, b, e), c, m (a, d, e)) для всех a , b , c , d , и е .
- Элементы идентичности : m (0, a , 1) = a для всех a .
Закон распределения может быть заменен законом ассоциации: [10]
- Ассоциативность : m ( x , w , m ( y , w , z )) = m ( m ( x , w , y ), w , z )
Операция median также может использоваться для определения понятия интервалов для распределительных решеток:
- I ( a , b ) = { x | m (a, x, b) = x } = { x | a ∧ b ≤ x ≤ a ∨ b }. [11]
Граф конечной дистрибутивной решетки имеет ребро между вершинами a и b, если I ( a , b ) = { a , b }. Для каждых двух вершин a и b этого графа интервал I ( a , b ), определенный выше в терминах теории решетки, состоит из вершин на кратчайших путях от a до b и, таким образом, совпадает с теоретико-графовыми интервалами, определенными ранее. Для каждых трех элементов решетки , б и с , м( a , b , c ) - единственное пересечение трех интервалов I ( a , b ), I ( a , c ) и I ( b , c ). [12] Следовательно, граф произвольной конечной дистрибутивной решетки является медианным графом. И наоборот, если медианный граф G содержит две вершины 0 и 1 такие, что каждая другая вершина лежит на кратчайшем пути между ними (эквивалентно, m (0, a , 1) = a для всех a), то мы можем определить дистрибутивную решетку, в которой a ∧ b = m ( a , 0, b ) и a ∨ b = m ( a , 1, b ), и G будет графиком этой решетки. [13]
Duffus & Rival (1983) характеризует графы дистрибутивных решеток непосредственно как сохраняющие диаметр ретракты гиперкубов. В более общем смысле, каждый медианный граф порождает тернарную операцию m, удовлетворяющую идемпотентности, коммутативности и дистрибутивности, но, возможно, без элементов идентичности дистрибутивной решетки. Каждая тернарная операция на конечном множестве, удовлетворяющем этим трем свойствам (но не обязательно имеющим 0 и 1 элементы), аналогичным образом порождает медианный граф. [14]
Выпуклые множества и семейства Хелли [ править ]
В средней графе, набор S вершин называется выпуклой , если для любых двух вершин и б , принадлежащих к S , весь интервал I ( , б ) представляет собой подмножество S . Эквивалентно, учитывая два определения интервалов выше, S является выпуклым , если она содержит все кратчайший путь между двумя из его вершин, или если она содержит медиану каждый набор из трех точек , по меньшей мере , две из которых взято из S . Заметим, что пересечение каждой пары выпуклых множеств само выпукло. [15]
Выпуклые множества в медианном графе обладают свойством Хелли : если F - произвольное семейство попарно пересекающихся выпуклых множеств, то все множества в F имеют общее пересечение. [16] В самом деле , если F имеет только три выпуклых множества S , T и U в нем, причем a находится в пересечении пары S и T , b в пересечении пары T и U и c в пересечении пару S и U , то каждый кратчайший путь изот a до b должны лежать внутри T по выпуклости, и аналогично каждый кратчайший путь между двумя другими парами вершин должен лежать внутри двух других наборов; но m ( a , b , c ) принадлежит путям между всеми тремя парами вершин, поэтому он лежит внутри всех трех наборов и составляет часть их общего пересечения. Если F имеет более трех выпуклых множеств в нем, результат следует индукцией по количеству множеств, так как можно заменить произвольную пару множеств в F их пересечением, используя результат для троек множеств, чтобы показать, что замененное семейство все еще попарно пересекается.
Особенно важным семейством выпуклых множеств в медианном графе, играющим роль, аналогичную роли полупространств в евклидовом пространстве, являются множества
- W uv = { w | d ( w , u ) < d ( w , v )}
для каждого ребра uv графа. Другими словами, W uv состоит из вершин, более близких к u, чем к v , или, что то же самое, из вершин w таких, что некоторый кратчайший путь из v в w проходит через u . Чтобы показать, что W uv выпуклый, пусть w 1 w 2 ... w k - произвольный кратчайший путь, который начинается и заканчивается в W uv ; тогда w 2 также должен лежать внутри W uv , иначе две точкиm 1 = m ( u , w 1 , w k ) и m 2 = m ( m 1 , w 2 ... w k ) можно было бы показать (рассматривая возможные расстояния между вершинами) как различные медианы u , w 1 и w k , что противоречит определению медианного графа, которое требует, чтобы медианы были уникальными. Таким образом, каждая последующая вершина кратчайшего пути между двумя вершинами W uv также лежит в W uv, поэтому W uv содержит все кратчайшие пути между его узлами, одно из определений выпуклости.
Свойство Хелли для множеств W uv играет ключевую роль в описании медианных графов как решения примеров 2-выполнимости, описанных ниже.
2-выполнимость [ править ]
Медианные графы тесно связаны с наборами решений задач 2-выполнимости, которые могут использоваться как для характеристики этих графов, так и для связи их с сохраняющими смежность отображениями гиперкубов. [17]
Экземпляр 2-выполнимости состоит из набора логических переменных и набора предложений , ограничений на определенные пары переменных, требующих от этих двух переменных избегать определенных комбинаций значений. Обычно такие проблемы выражаются в соединительной нормальной форме , в которой каждое предложение выражается как дизъюнкция, а весь набор ограничений выражается как соединение предложений, например
Решением такого случая является присвоение значений истинности переменным, удовлетворяющим всем условиям, или, что то же самое, которое заставляет выражение конъюнктивной нормальной формы для этого экземпляра становиться истинным, когда в него подставляются значения переменных. Семейство всех решений имеет естественную структуру как медианную алгебру, где медиана трех решений формируется путем выбора каждого значения истинности в качестве функции большинства значений в трех решениях; несложно проверить, что это медианное решение не может нарушить ни одно из положений. Таким образом, эти решения образуют медианный граф, в котором сосед каждого решения формируется путем отрицания набора переменных, которые все ограничены, чтобы быть равными или неравными друг другу.
И наоборот, каждый медианный граф G может быть представлен таким образом как решение, установленное для экземпляра 2-выполнимости. Чтобы найти такое представление, создайте экземпляр 2-выполнимости, в котором каждая переменная описывает ориентацию одного из ребер в графе (назначение направления ребру, заставляющее граф становиться направленным, а не ненаправленным), и каждое ограничение позволяет два ребра разделяют пару ориентаций только тогда, когда существует вершина v такая, что обе ориентации лежат на кратчайших путях от других вершин к v . Каждая вершина v из G соответствует решению этого экземпляра 2-выполнимости , в котором все ребра направлены против. Таким образом, каждое решение экземпляра должно исходить из некоторой вершины v , где v - общее пересечение множеств W uw для ребер, направленных от w к u ; это общее пересечение существует благодаря свойству Хелли множеств W uw . Таким образом, решение этой 2-выполнимость инстанция соответствует один к одному с вершинами G .
Втягивания гиперкубов [ править ]
Втягивания графы G является смежностью отображения , сохраняющей от G к одному из его подграфов. [18] Точнее, это гомоморфизм графов φ из G в себя такой, что φ ( v ) = v для каждой вершины v в подграфе φ (G). Изображение ретракции называется ретрактом из G . Ретракции являются примерами метрических карт : расстояние между φ ( v ) и φ ( w ) для любых v и w не более чем равно расстоянию между vи w , и равно, если оба v и w принадлежат φ ( G ). Таким образом, отводной должен быть изометрический подграф из G : расстояния в ретракции равны те , в G .
Если G - медианный граф, а a , b и c - произвольные три вершины ретракта φ ( G ), то φ ( m ( a , b , c )) должно быть медианой a , b и c , а значит, должно равняться m ( a , b , c ). Следовательно, φ ( G ) содержит медианы всех троек своих вершин и также должен быть медианным графом. Другими словами, семейство медианных графов замыкается при операции ретракции. [19]
Гиперкуба графа , в котором вершины соответствуют всем возможным к -разрядных битвекторов и в котором две вершины смежны , когда соответствующие битвекторов отличаются только одним битом, является частным случаем K сетки графа n - мерного и, следовательно , средний график. Медиана трех битовых векторов a , b и c может быть вычислена путем вычисления в каждой битовой позиции функции большинства битов a , b и c . Поскольку медианные графы закрываются при ретракции и включают гиперкубы, каждый ретракт гиперкуба является медианным графом.
И наоборот, каждый медианный граф должен быть ретрактом гиперкуба. [20] Это можно увидеть из связи, описанной выше, между медианными графами и 2-выполнимостью: пусть G- граф решений для случая 2-выполнимости; без потери общности этот пример можно сформулировать таким образом, что никакие две переменные не всегда равны или всегда неравны в каждом решении. Тогда пространство всех присвоений истинности переменным этого экземпляра образует гиперкуб. Для каждого предложения, сформированного как дизъюнкция двух переменных или их дополнений, в экземпляре 2-выполнимости можно сформировать ретракцию гиперкуба, в котором присвоения истинности, нарушающие это предложение, отображаются в назначения истинности, в которых обе переменные удовлетворяют условию, без изменения других переменных в присвоении истинности. Композиция ретракций, сформированных таким образом для каждого из предложений, дает ретракцию гиперкуба на пространство решений экземпляра и, следовательно, дает представлениеG как ретракт гиперкуба. В частности, медианные графы являются изометрическими подграфами гиперкубов и, следовательно, являются частичными кубами . Однако не все частичные кубы являются медианными графами; например, циклический граф с шестью вершинами - это частичный куб, но не медианный граф.
Как описывают Имрих и Клавжар (2000) , изометрическое вложение медианного графа в гиперкуб можно построить за время O ( m log n ), где n и m - количество вершин и ребер графа соответственно. [21]
Графики без треугольников и алгоритмы распознавания [ править ]
Проблемы проверки того, является ли граф медианным графом и является ли граф свободным от треугольников , были хорошо изучены, когда Имрих, Клавжар и Малдер (1999) заметили, что в некотором смысле они эквивалентны в вычислительном отношении. [22] Следовательно, наиболее известная временная граница для проверки того, является ли граф свободным от треугольников, O ( m 1,41 ), [23] также применима к проверке того, является ли граф медианным графом, а также к любым улучшениям в алгоритмах проверки медианного графа. также приведет к улучшению алгоритмов обнаружения треугольников на графах.
В одном направлении, предположим, что на входе дан граф G , и он должен проверить, не содержит ли G треугольников. Из G , построить новый граф H , имеющий в качестве вершин каждый набор ноль, один или два смежных вершин G . Два таких множества смежны в H, если они отличаются ровно на одну вершину. Эквивалентное описание Н является то , что она образована путем разделения каждого ребро G в пути двух краев, и добавлении новой вершины , соединенную со всеми оригинальными вершинами G . Этот граф H по построению является частичным кубом, но он является медианным графом только тогда, когда Gне содержит треугольников: если a , b и c образуют треугольник в G , то { a , b }, { a , c } и { b , c } не имеют медианы в H , поскольку такая медиана должна соответствует множеству { в , б , с }, но наборы из трех или более вершин G не образуют вершины в H . Следовательно, G не имеет треугольников тогда и только тогда, когда H - медианный граф. В случае, если G не содержит треугольников,H - его симплексный граф . Алгоритм для эффективной проверки того, является ли H медианным графом, может с помощью этой конструкции также использоваться для проверки того, не содержит ли G треугольников. Это преобразование сохраняет вычислительную сложность задачи, для размера H пропорциональна , что из G .
Снижение в другом направлении, от обнаружения треугольников до тестирования медианного графа, является более сложным и зависит от предыдущего алгоритма распознавания медианного графа Хагауэра, Имриха и Клавжара (1999) , который проверяет несколько необходимых условий для медианного графа за почти линейное время. . Ключевой новый шаг предполагает использование поиска в ширинудля разделения вершин графа на уровни в соответствии с их расстояниями от произвольно выбранной корневой вершины, формирование графа из каждого уровня, в котором две вершины являются смежными, если они имеют общего соседа на предыдущем уровне, и поиск треугольников в этих графах. Медиана любого такого треугольника должна быть общим соседом трех вершин треугольника; если этот общий сосед не существует, граф не является медианным графом. Если все треугольники, найденные таким образом, имеют медианы, и предыдущий алгоритм обнаруживает, что граф удовлетворяет всем остальным условиям для того, чтобы быть медианным графом, тогда это должен быть медианный граф. Этот алгоритм требует не только возможности проверить, существует ли треугольник, но и списка всех треугольников в графе уровней. В произвольных графах для перечисления всех треугольников иногда требуется Ω (м 3/2 ) времени, так как некоторые графики содержат такое количество треугольников, однако Hagauer et al. показывают, что количество треугольников, возникающих на графиках уровней их редукции, почти линейно, что позволяет Alon et al. Метод быстрого матричного умножения для поиска используемых треугольников.
Эволюционные деревья, графы Бунемана и сплит-системы Хелли [ править ]
Филогения - это вывод эволюционных деревьев из наблюдаемых характеристик видов ; такое дерево должно располагать виды в различных вершинах и может иметь дополнительные скрытые вершины , но скрытые вершины должны иметь три или более инцидентных ребра и также должны быть помечены характеристиками. Характеристика является бинарной, если она имеет только два возможных значения, а набор видов и их характеристик демонстрируют идеальную филогению.когда существует эволюционное дерево, в котором вершины (виды и скрытые вершины), помеченные любым конкретным значением характеристики, образуют непрерывное поддерево. Если невозможно построить дерево с совершенной филогенией, часто желательно найти такое дерево, которое демонстрирует максимальную экономичность или, что эквивалентно, минимизирует количество раз, когда конечные точки ребра дерева имеют разные значения одной из характеристик, суммированных по всем ребрам и всем. характеристики.
Бунеман (1971) описал метод вывода идеальной филогении бинарных характеристик, если они существуют. Его метод естественным образом обобщается на построение медианного графа для любого набора видов и бинарных характеристик, который был назван медианной сетью или графом Бунемана [24] и представляет собой тип филогенетической сети.. Каждое эволюционное дерево максимальной экономии встраивается в граф Бунемана в том смысле, что ребра дерева следуют по путям в графе, а количество изменений характеристических значений на краю дерева совпадает с числом в соответствующем пути. Граф Бунемана будет деревом тогда и только тогда, когда существует совершенная филогения; это происходит, когда нет двух несовместимых характеристик, для которых соблюдаются все четыре комбинации значений характеристик.
Чтобы сформировать граф Бунемана для набора видов и характеристик, сначала удалите повторяющиеся виды, которые неотличимы от некоторых других видов, и повторяющиеся характеристики, которые всегда совпадают с некоторыми другими характеристиками. Затем сформируйте скрытую вершину для каждой комбинации значений характеристик, чтобы каждые два значения существовали в некоторых известных видах. В показанном примере есть маленькие коричневые бесхвостые мыши, маленькие серебристые бесхвостые мыши, маленькие коричневохвостые мыши, большие коричневохвостые мыши и большие серебристохвостые мыши; метод графа Бунемана формирует скрытую вершину, соответствующую неизвестному виду маленьких серебристых мышей, потому что каждая попарная комбинация (маленькая и серебристая, маленькая и хвостатая, серебристая и хвостатая) наблюдается у некоторых других известных видов. Тем не мение,этот метод не позволяет сделать вывод о существовании больших коричневых бесхвостых мышей, потому что не известно ни одной мыши, обладающей одновременно большими и бесхвостыми признаками. Как только скрытые вершины определены, сформируйте ребро между каждой парой видов или скрытых вершин, которые различаются одной характеристикой.
Можно эквивалентно описать набор бинарных характеристик как систему разделения , семейство наборов, обладающих тем свойством, что дополнительный набор каждого набора в семействе также входит в семейство. В этой сплит-системе есть набор для каждого значения характеристики, состоящий из видов, которые имеют это значение. Когда скрытые вершины включены, результирующая система разделения обладает свойством Helly : каждое попарно пересекающееся подсемейство имеет общее пересечение. В некотором смысле медианные графы характеризуются как происходящие из расщепленных систем Хелли: пары ( W uv , W vu ), определенные для каждого ребра uvмедианного графа образуют расщепленную систему Хелли, поэтому, если применить конструкцию графа Бунемана к этой системе, скрытые вершины не потребуются, и результат будет таким же, как и у исходного графа. [25]
Bandelt et al. (1995) и Bandelt, Macaulay & Richards (2000) описывают методы упрощенного ручного вычисления графа Бунемана и используют эту конструкцию для визуализации генетических взаимоотношений человека.
Дополнительные свойства [ править ]
- Декартово произведение каждых два срединных графиков является еще одним медианным графом. Медианы в графе продукта могут быть вычислены путем независимого нахождения медиан в двух факторах, так же как медианы в графах сетки могут быть вычислены путем независимого нахождения медианы в каждом линейном измерении.
- Windex графа измеряет количество опережающего просмотра , необходимого для оптимального решить проблему , в которой одна дана последовательность вершин графа ев I , и должны найти в качестве вывода другой последовательности вершин т I сведение к минимуму сумма расстояний d ( ы I , t i ) и d ( t i - 1 , t i ) . Медианные графы - это именно те графы, которые имеют Windex 2. В медианном графе оптимальным выбором является установка t i = m (t i - 1 , s i , s i + 1 ) . [1]
- Свойство уникальной медианы также называется уникальным свойством точки Штейнера . [1] Оптимальное дерево Штейнера для трех вершин a , b и c в медианном графе может быть найдено как объединение трех кратчайших путей от a , b и c к m ( a , b , c ). Bandelt и Barthélémy (1984) в более общем плане изучают проблему поиска вершины, минимизирующую сумму расстояний.для каждой из заданного набора вершин и покажите, что у него есть уникальное решение для любого нечетного числа вершин в медианном графе. Они также показывают , что медиана множества S вершин в медиане графа удовлетворяет критерий Кондорса для победитель выборов : по сравнению с любой другой вершиной, он ближе к большинству вершин в S .
- Как и в случае с частичными кубами в более общем смысле, каждый медианный граф с n вершинами имеет не более ( n / 2) log 2 n ребер. Однако количество ребер не может быть слишком маленьким: Клавжар, Малдер и Шкрековски (1998) доказывают, что в каждом медианном графе выполняется неравенство 2 n - m - k ≤ 2 , где m - количество ребер, а k - размерность гиперкуб, ретрактом которого является граф. Это неравенство является равенством тогда и только тогда, когда медианный граф не содержит кубов. Это следствие другого тождества для медианных графов: эйлеровой характеристики Σ (-1)dim ( Q ) всегда равен единице, где сумма берется по всем подграфам гиперкуба Q данного медианного графа. [26]
- Единственные регулярные медианные графы - это гиперкубы. [27]
- Каждый медианный граф является модульным графом . Модульные графы - это класс графов, в которых каждая тройка вершин имеет медиану, но не обязательно, чтобы медианы были уникальными. [28]
Примечания [ править ]
- ^ a b c Чунг, Грэм и Сакс (1987) .
- ^ Бунемановская (1971) ; Платье и др. (1997) ; Платье, Huber & Moulton (1997) .
- ^ Bandelt & Barthélémy (1984) ; Дэй и МакМоррис (2003) .
- ^ Имрих & Klavžar (2000) , предложение 1.26, стр. 24.
- ^ Это непосредственно следует из характеристики медианных графов как ретрактов гиперкубов, описанной ниже.
- ^ Солтан, Замбицкий и Присэкару (1973) ; Чепои, Драган и Ваксес (2002) ; Чепои, Fanciullini и Vaxès (2004) .
- ^ Klavžar & Škrekovski (2000) .
- ^ Бартелеми, Леклерк и Monjardet (1986) , стр 200.
- ↑ Birkhoff & Kiss (1947) приписывают определение этой операции Биркгофу, Г. (1940), Теория решеток , Американское математическое общество, стр. 74.
- ^ Кнут (2008) , стр. 65 и упражнения 75 и 76 на стр. 89–90. Кнут утверждает, что простое доказательство того, что ассоциативность подразумевает дистрибутивность, остается неизвестным.
- ^ Эквивалентность между двумя выражениями в этом уравнении, одно в терминах медианной операции, а другое в терминах операций и неравенств решетки, является теоремой 1 Биркгофа и Кисс (1947) .
- ↑ Birkhoff & Kiss (1947) , теорема 2.
- ↑ Birkhoff & Kiss (1947) , стр. 751.
- ^ Avann (1961) .
- ^ Knuth (2008) называет такое множество идеалом , но выпуклое множество в графе дистрибутивной решетки - это не то же самое, что идеал решетки .
- ^ Имрих и Клавжар (2000) , теорема 2.40, стр. 77.
- ^ Bandelt & Чепа (2008) , предложение 2.5, с.8; Чанг, Грэм и Сакс (1989) ; Федер (1995) ; Knuth (2008) , теорема S, стр. 72.
- ↑ Ад (1976) .
- ^ Имрих & Klavžar (2000) , предложение 1.33, стр. 27.
- ^ Бандельт (1984) ; Имрих и Клавжар (2000) , теорема 2.39, с.76; Кнут (2008) , стр. 74.
- ^ Техника, кульминацией которой является лемма 7.10 на стр. 218 Имриха и Клавжара, состоит в применении алгоритма Чибы и Нишизеки (1985) для перечисления всех 4-циклов в графе G , формируя неориентированный граф, имеющий в качестве вершин рёберграфа G, имеющий в качестве ребер противоположные стороны 4-цикла, и использующий компоненты связности этого производного графа для формирования координат гиперкуба. Эквивалентный алгоритм - Knuth (2008) , Algorithm H, p. 69.
- ^ Предыдущие алгоритмы распознавания медианного графа см. В Jha & Slutzki (1992) , Imrich & Klavžar (1998) и Hagauer, Imrich & Klavžar (1999) . Об алгоритмах обнаружения треугольников см. Itai & Rodeh (1978) , Chiba & Nishizeki (1985) и Alon, Yuster & Zwick (1995) .
- ^ Алон, Юстер и Цвик (1995) , основанный на быстром умножении матриц . Здесь m - количество ребер в графе, а большая нотация O скрывает большой постоянный множитель; лучшие практические алгоритмы обнаружения треугольника занимают время O ( м 3/2 ). Для распознавания медианного графа временная граница может быть выражена либо через m, либо через n (количество вершин), как m = O ( n log n ).
- ^ Малдер и Шрайвер (1979) описали версию этого метода для систем характеристик, не требующих скрытых вершин, а Бартелеми (1989) дает полную конструкцию. Название графа Бунемана дано в Dress et al. (1997) и платье, Huber & Moulton (1997) .
- ^ Малдер и Шрайвер (1979) .
- ^ Škrekovski (2001) .
- ^ Малдер (1980) .
- ^ Модульные графы , Информационная система по классам графов и их включениям, получено 30 сентября 2016 г.
Ссылки [ править ]
- Алон, Нога ; Юстер, Рафаэль; Цвик, Ури (1995), "Цвет-кодирование", Журнал ACM , 42 (4): 844-856, DOI : 10,1145 / 210332,210337 , МР 1411787 , S2CID 208936467.
- Avann, ИП (1961), "Метрические тройные распределительные полуструктурами", Труды Американского математического общества , 12 (3): 407-414, DOI : 10,2307 / 2034206 , JSTOR 2034206 , MR 0125807.
- Bandelt, Ханс-Юрген (1984), "Ретракты гиперкубов", Журнал теории графов , 8 (4): 501-510, DOI : 10.1002 / jgt.3190080407 , МР 0766499.
- Бандельт, Ханс-Юрген; Бартелей, Жан-Пьер (1984), "Медиана в срединных графах", Дискретная прикладная математика , 8 (2): 131-142, DOI : 10.1016 / 0166-218X (84) 90096-9 , МР 0743019.
- Бандельт, Ханс-Юрген; Чепой, Виктор (2008), «Метрическая теория графов и геометрия: обзор» (PDF) , Обзоры по дискретной и вычислительной геометрии , Современная математика, 453 , Провиденс, Род-Айленд: Американское математическое общество, стр. 49–86, DOI : 10.1090 / conm / 453/08795 , ISBN 9780821842393, Руководство по ремонту 2405677.
- Бандельт, Ханс-Юрген; Forster, P .; Сайкс, Британская Колумбия; Ричардс, Мартин Б. (1 октября 1995 г.), "Митохондриальные портреты популяций людей с использованием медианных сетей" , Genetics , 141 (2): 743–753, PMC 1206770 , PMID 8647407.
- Бандельт, Ханс-Юрген; Forster, P .; Рол, Arne (1 января 1999), "Медиана-присоединение сетей для выводя внутривидовые филогенез" , Молекулярная биология и эволюция , 16 (1): 37-48, DOI : 10,1093 / oxfordjournals.molbev.a026036 , PMID 10331250.
- Бандельт, Ханс-Юрген; Маколей, Винсент; Ричардс, Мартин Б. (2000), «Медианные сети: быстрое построение и жадное сокращение, одно моделирование и два тематических исследования на основе мтДНК человека», Molecular Phylogenetics and Evolution , 16 (1): 8–28, CiteSeerX 10.1.1.128. 3232 , DOI : 10,1006 / mpev.2000.0792 , PMID 10877936.
- Бартелеми, Жан-Пьер (1989), «От копировальных гиперграфов к медианным графам со скрытыми вершинами», Дискретная математика , 76 (1): 9–28, DOI : 10.1016 / 0012-365X (89) 90283-5 , MR 1002234.
- Barthélemy, J.P .; Leclerc, B .; Monjardet, В. (1986), "Об использовании упорядоченных множеств в задачах сравнения и консенсуса классификаций", журнал классификации , 3 (2): 187-224, DOI : 10.1007 / BF01894188 , S2CID 6092438.
- Биркгоф, Гарретт ; Поцелуй, SA (1947), "Тройная операция в дистрибутивных решеток" , Бюллетень Американского математического общества , 53 (1): 749-752, DOI : 10,1090 / S0002-9904-1947-08864-9 , MR 0021540.
- Бунеман, П. (1971), «Восстановление деревьев по мерам несходства», в Hodson, FR; Kendall, DG; Tautu, PT (eds.), Математика в археологических и исторических науках , Edinburgh University Press, стр. 387–395.
- Чепой, В .; Dragan, F .; Vaxès, Y. (2002), "Проблемы центра и диаметра в плоских четырехугольниках и триангуляциях", Proc. 13-й симпозиум ACM-SIAM по дискретным алгоритмам , Soda '02, стр. 346–355 , ISBN 9780898715132.
- Чепой, В .; Fanciullini, C .; Ваксес, Ю. (2004), "Медианная проблема в некоторых плоских триангуляциях и четырехангуляциях", Computational Geometry: Theory & Applications , 27 (3): 193–210, doi : 10.1016 / j.comgeo.2003.11.002.
- Chiba, N .; Nishizeki, Т. (1985), "Arboricity и алгоритмы подграф листинга", SIAM журнал по вычислениям , 14 : 210-223, DOI : 10,1137 / 0214017 , MR 0774940.
- Чанг, ФРК ; Graham, RL ; Сакс, ME (1987), «Динамический поиск в графах», в Wilf, H. (ed.), Discrete Algorithms and Complexity (Kyoto, 1986) (PDF) , Perspectives in Computing, 15 , New York: Academic Press, стр. 351–387, MR 0910939.
- Чанг, ФРК ; Graham, RL ; Сакс, ME (1989), "Динамическая задача размещения графов" (PDF) , Combinatorica , 9 (2): 111-132, дои : 10.1007 / BF02124674 , S2CID 5419897.
- День, Уильям HE; Макморрис, FR (2003), Аксиоматическая теория консенсуса в групповом выборе и биоинформатике , Общество промышленной и прикладной математики, стр. 91–94, ISBN 978-0-89871-551-4.
- Платье, А .; Хенди, М .; Huber, K .; Моултона, V. (1997), "О количестве вершин и ребер графа бунемановского", Анналы Комбинаторики , 1 (1): 329-337, DOI : 10.1007 / BF02558484 , МР 1630739 , S2CID 120716928.
- Платье, А .; Huber, K .; Моултон, В. (1997), "Некоторые вариации на тему Бунеманом", Анналы Комбинаторика , 1 (1): 339-352, DOI : 10.1007 / BF02558485 , МР 1630743 , S2CID 122966547.
- Даффус, Дуайт ; Конкурент, Иван (1983), "Графы ориентируем в качестве дистрибутивных решеток", Труды Американского математического общества , 88 (2): 197-200, DOI : 10,2307 / 2044697 , JSTOR 2044697.
- Федер Т. (1995), Стабильные сети и графы продуктов , Мемуары Американского математического общества, 555.
- Хагауэр, Иоганн; Имрих, Вильфрид; Klavžar, Санди (1999), "признавая срединные графики в subquadratic времени", Теоретическая информатика , 215 (1-2): 123-136, DOI : 10.1016 / S0304-3975 (97) 00136-9 , MR 1678773.
- Ад, Павол (1976), « Уменьшение графов», Colloquio Internazionale sulle Teorie Combinatorie (Roma, 1973), Tomo II , Atti dei Convegni Lincei, 17 , Рим: Accad. Наз. Lincei, стр. 263–268, MR 0543779.
- Имрих, Вильфрид; Klavžar, Санди (1998), "A выпуклости лемма и расширение процедура для двудольных графов", Европейский журнал Комбинаторики , 19 (6): 677-686, DOI : 10,1006 / eujc.1998.0229 , МР 1642702.
- Имрих, Вильфрид; Клавжар, Санди (2000), Графики продуктов: структура и распознавание , Wiley, ISBN 978-0-471-37039-0, Руководство MR 0788124.
- Имрих, Вильфрид; Клавжар, Санди; Малдер, Генри Мартин (1999), "Срединные графики и треугольник свободных графов", SIAM журнал по дискретной математике , 12 (1): 111-118, CiteSeerX 10.1.1.28.5906 , DOI : 10,1137 / S0895480197323494 , МР 1666073.
- Itai, A .; Rodeh, М. (1978), "Нахождение минимальной цепи в графе", СИ журнал по вычислениям , 7 (4): 413-423, DOI : 10,1137 / 0207033 , МР 0508603.
- Jha, Pranava K .; Слуцки, Гиора (1992), "Алгоритмы выпуклого расширения для распознавания и изометрического вложения медианных графов", Ars Combinatoria , 34 : 75–92, MR 1206551.
- Клавжар, Санди; Малдер, Генри Мартин (1999), «Медианные графы: характеристики, теория местоположений и связанные структуры», Журнал комбинаторной математики и комбинаторных вычислений , 30 : 103–127, MR 1705337.
- Клавжар, Санди; Малдер, Генри Мартин; Škrekovski, Riste (1998), "Об Эйлер-тип формула для срединных графов", дискретная математика , 187 (1): 255-258, DOI : 10.1016 / S0012-365X (98) 00019-3 , МР 1630736.
- Клавжар, Санди; Škrekovski, Riste (2000), "О срединных графиков и срединных графиков сетки", Дискретная математика , 219 (1-3): 287-293, DOI : 10.1016 / S0012-365X (00) 00085-6 , MR 1761732.
- Кнут, Дональд Э. (2008), «Медианные алгебры и медианные графы», Искусство компьютерного программирования , IV, Часть 0: Введение в комбинаторные алгоритмы и булевы функции, Аддисон-Уэсли, стр. 64–74, ISBN 978-0-321-53496-5.
- Малдер, Генри Мартин (1980), " п -кубов и медианный граф", Журнал теории графов , 4 (1): 107-110, DOI : 10.1002 / jgt.3190040112 , МР 0558458.
- Малдер, Генри Мартин; Шрайвер, Александр (1979), «Медианные графы и гиперграфы Хелли» , Дискретная математика , 25 (1): 41–50, DOI : 10.1016 / 0012-365X (79) 90151-1 , MR 0522746.
- Небески, Ладислав (1971), «Медианные графы», Commentationes Mathematicae Universitatis Carolinae , 12 : 317–325, MR 0286705.
- Шкрековски, Ристе (2001), «Два отношения для медианных графов», Дискретная математика , 226 (1): 351–353, DOI : 10.1016 / S0012-365X (00) 00120-5 , MR 1802603.
- Soltan, P .; Замбицкий, Д .; Присэкару К. (1973), Экстремальные задачи на графах и алгоритмы их решения , Кишинев: Ştiinţa..
Внешние ссылки [ править ]
- Медианные графы , Информационная система для включений классов графов.
- Сеть , бесплатное программное обеспечение для филогенетической сети. Сеть генерирует эволюционные деревья и сети на основе генетических, лингвистических и других данных.
- PhyloMurka , программное обеспечение с открытым исходным кодом для вычислений медианной сети на основе биологических данных.