Теория массового обслуживания

Сети очередей - это системы, в которых отдельные очереди соединены сетью маршрутизации. На этом изображении серверы представлены кружками, очереди - серией прямоугольников, а сеть маршрутизации - стрелками. При изучении сетей с очередями обычно пытаются получить равновесное распределение сети, хотя во многих приложениях изучение переходного состояния является фундаментальным.

Теория массового обслуживания - это математическое исследование очередей или очередей . ^[1] Модель организации очередей построена так, чтобы можно было спрогнозировать длину очереди и время ожидания. ^[1] Теория массового обслуживания обычно считается разделом исследования операций, потому что результаты часто используются при принятии бизнес-решений о ресурсах, необходимых для предоставления услуги.

Теория массового обслуживания берет свое начало в исследованиях, проведенных Агнером Крарупом Эрлангом, когда он создал модели для описания системы датской компании Copenhagen Telephone Exchange. ^[1] С тех пор идеи нашли применение, включая телекоммуникации , транспортную инженерию , вычисления ^[2] и, особенно, в промышленном строительстве , при проектировании заводов, магазинов, офисов и больниц, а также в управлении проектами. ^{[3] [4]}

Правописание [ править ]

Написание «в очереди» над «очередью» обычно встречается в области академических исследований. Фактически, одним из флагманских журналов в этой области является Queuing Systems .

Одиночные узлы очередей [ править ]

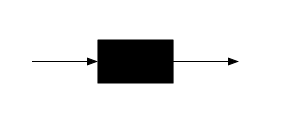
Очередь или узел очередей можно рассматривать как почти черный ящик . Задания или «клиенты» прибывают в очередь, возможно, ждут какое-то время, им требуется некоторое время для обработки, а затем удаляются из очереди.

Черный ящик. Задания приходят в очередь и уходят из нее.

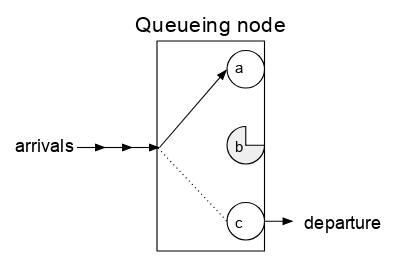
Однако узел очереди - это не совсем чистый черный ящик, поскольку требуется некоторая информация о внутренней части узла очереди. В очереди есть один или несколько «серверов», каждый из которых может быть связан с поступающим заданием до тех пор, пока он не уйдет, после чего этот сервер будет свободен для соединения с другим поступающим заданием.

Узел очередей с 3 серверами. Сервер a простаивает, поэтому ему передается поступление на обработку. Сервер b в настоящее время занят, и ему потребуется некоторое время, прежде чем он сможет завершить выполнение своей работы. Сервер c только что завершил обслуживание задания и, следовательно, будет следующим, чтобы получить поступившее задание.

Часто используется аналогия с кассиром в супермаркете. Существуют и другие модели, но эта часто встречается в литературе. Клиенты прибывают, обрабатываются кассиром и уходят. Каждый кассир обрабатывает одного клиента за раз, и, следовательно, это узел очереди только с одним сервером. Настройка, при которой покупатель немедленно уходит, если кассир занят, когда приходит покупатель, называется очередью без буфера (или без «зоны ожидания», или аналогичных терминов). Настройка с зоной ожидания для n заявок называется очередью с буфером размера n .

Процесс рождения-смерти [ править ]

Поведение отдельной очереди (также называемой «узлом очереди») можно описать процессом рождения-смерти , который описывает поступления и выбывания из очереди, а также количество заданий (также называемых «клиентами» или «запросами». "или любое количество других вещей, в зависимости от поля), которое в настоящее время находится в системе. Прибытие увеличивает количество работ на 1, а отъезд (работа, завершающая свое обслуживание) уменьшает k на 1.

Уравнения баланса [ править ]

Уравнения установившегося состояния для процесса рождения и смерти, известные как уравнения баланса , следующие. Здесь обозначает вероятность устойчивого состояния нахождения в состоянии n .${\displaystyle P_{n}}$

${\displaystyle \mu _{1}P_{1}=\lambda _{0}P_{0}}$

${\displaystyle \lambda _{0}P_{0}+\mu _{2}P_{2}=(\lambda _{1}+\mu _{1})P_{1}}$

${\displaystyle \lambda _{n-1}P_{n-1}+\mu _{n+1}P_{n+1}=(\lambda _{n}+\mu _{n})P_{n}}$

Первые два уравнения подразумевают

${\displaystyle P_{1}={\frac {\lambda _{0}}{\mu _{1}}}P_{0}}$

а также

${\displaystyle P_{2}={\frac {\lambda _{1}}{\mu _{2}}}P_{1}+{\frac {1}{\mu _{2}}}(\mu _{1}P_{1}-\lambda _{0}P_{0})={\frac {\lambda _{1}}{\mu _{2}}}P_{1}={\frac {\lambda _{1}\lambda _{0}}{\mu _{2}\mu _{1}}}P_{0}.}$

По математической индукции

${\displaystyle P_{n}={\frac {\lambda _{n-1}\lambda _{n-2}\cdots \lambda _{0}}{\mu _{n}\mu _{n-1}\cdots \mu _{1}}}P_{0}=P_{0}\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}.}$

Состояние приводит к:${\displaystyle \sum _{n=0}^{\infty }P_{n}=P_{0}+P_{0}\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}=1}$

${\displaystyle P_{0}={\frac {1}{1+\sum _{n=1}^{\infty }\prod _{i=0}^{n-1}{\frac {\lambda _{i}}{\mu _{i+1}}}}},}$

которое вместе с уравнением для полностью описывает требуемые вероятности установившегося состояния.${\displaystyle P_{n}}$ ${\displaystyle (n\geq 1)}$

Обозначения Кендалла [ править ]

Одиночные узлы очередей обычно описываются с использованием нотации Кендалла в форме A / S / c, где A описывает распределение продолжительности между каждым поступлением в очередь, S распределение времени обслуживания для заданий и c количество серверов в узле. ^{[5] [6]} В качестве примера обозначения очередь M / M / 1 представляет собой простую модель, в которой один сервер обслуживает задания, которые поступают в соответствии с процессом Пуассона (где длительность между поступлениями распределяется экспоненциально ) и экспоненциально время распределенного обслуживания (M обозначает марковский процесс ). ВОчередь M / G / 1 , G означает «общий» и указывает произвольное распределение вероятностей для времени обслуживания.

Пример анализа очереди M / M / 1 [ править ]

Рассмотрим очередь с одним сервером и следующими характеристиками:

• λ : частота прибытия (ожидаемое время между прибытием каждого клиента, например, 30 секунд);
• μ : величина, обратная среднему времени обслуживания (ожидаемое количество последовательных завершений обслуживания за одно и то же время, например, за 30 секунд);
• n : параметр, характеризующий количество клиентов в системе;
• P _n : вероятность наличия n клиентов в системе в устойчивом состоянии.

Далее, пусть E _n представляет количество раз, когда система входит в состояние n , а L _n представляет количество раз, когда система выходит из состояния n . Тогда для всех n , | E _n - L _n | ∈ {0, 1}. То есть количество раз, когда система покидает состояние, отличается не более чем на 1 от количества раз, когда она входит в это состояние, поскольку она либо вернется в это состояние в какой-то момент в будущем ( E _n = L _n ), либо нет. (| E _n - L _n | = 1).

Когда система переходит в установившееся состояние, скорость прибытия должна быть равна скорости отправления.

Таким образом, уравнения баланса

${\displaystyle \mu P_{1}=\lambda P_{0}}$

${\displaystyle \lambda P_{0}+\mu P_{2}=(\lambda +\mu )P_{1}}$

${\displaystyle \lambda P_{n-1}+\mu P_{n+1}=(\lambda +\mu )P_{n}}$

подразумевать

${\displaystyle P_{n}={\frac {\lambda }{\mu }}P_{n-1},\ n=1,2,\ldots }$

Тот факт, что приводит к формуле геометрического распределения${\displaystyle P_{0}+P_{1}+\cdots =1}$

${\displaystyle P_{n}=(1-\rho )\rho ^{n}}$

где ${\displaystyle \rho ={\frac {\lambda }{\mu }}<1.}$

Простая очередь с двумя уравнениями [ править ]

Обычная базовая система очередей приписывается Erlang и является модификацией закона Литтла . Учитывая частоту поступления λ , частоту отсева σ и частоту выбытия μ , длина очереди L определяется как:

${\displaystyle L={\frac {\lambda -\sigma }{\mu }}.}$

Assuming an exponential distribution for the rates, the waiting time W can be defined as the proportion of arrivals that are served. This is equal to the exponential survival rate of those who do not drop out over the waiting period, giving:

${\displaystyle {\frac {\mu }{\lambda }}=e^{-W{\mu }}}$

The second equation is commonly rewritten as:

${\displaystyle W={\frac {1}{\mu }}\mathrm {ln} {\frac {\lambda }{\mu }}}$

The two-stage one-box model is common in epidemiology.^[7]

Overview of the development of the theory[edit]

In 1909, Agner Krarup Erlang, a Danish engineer who worked for the Copenhagen Telephone Exchange, published the first paper on what would now be called queueing theory.^[8][9][10] He modeled the number of telephone calls arriving at an exchange by a Poisson process and solved the M/D/1 queue in 1917 and M/D/k queueing model in 1920.^[11] In Kendall's notation:

• M stands for Markov or memoryless and means arrivals occur according to a Poisson process;
• D stands for deterministic and means jobs arriving at the queue which require a fixed amount of service;
• k describes the number of servers at the queueing node (k = 1, 2, ...).

If there are more jobs at the node than there are servers, then jobs will queue and wait for service

The M/G/1 queue was solved by Felix Pollaczek in 1930,^[12] a solution later recast in probabilistic terms by Aleksandr Khinchin and now known as the Pollaczek–Khinchine formula.^[11][13]

After the 1940s queueing theory became an area of research interest to mathematicians.^[13] In 1953 David George Kendall solved the GI/M/k queue^[14] and introduced the modern notation for queues, now known as Kendall's notation. In 1957 Pollaczek studied the GI/G/1 using an integral equation.^[15] John Kingman gave a formula for the mean waiting time in a G/G/1 queue: Kingman's formula.^[16]

Leonard Kleinrock worked on the application of queueing theory to message switching in the early 1960s and packet switching in the early 1970s. His initial contribution to this field was his doctoral thesis at the Massachusetts Institute of Technology in 1962, published in book form in 1964. His theoretical work published in the early 1970s underpinned the use of packet switching in the ARPANET, a forerunner to the Internet.

The matrix geometric method and matrix analytic methods have allowed queues with phase-type distributed inter-arrival and service time distributions to be considered.^[17]

Systems with coupled orbits are an important part in queueing theory in the application to wireless networks and signal processing. ^[18]

Problems such as performance metrics for the M/G/k queue remain an open problem.^[11][13]

Service disciplines[edit]

Various scheduling policies can be used at queuing nodes:

First in first out

Also called first-come, first-served (FCFS),^[19] this principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.^[20]

Last in first out

This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first.^[20] Also known as a stack.

Processor sharing

Service capacity is shared equally between customers.^[20]

Priority

Customers with high priority are served first.^[20] Priority queues can be of two types, non-preemptive (where a job in service cannot be interrupted) and preemptive (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.^[21]

Shortest job first

The next job to be served is the one with the smallest size^[22]

Preemptive shortest job first

The next job to be served is the one with the original smallest size^[23]

Shortest remaining processing time

The next job to serve is the one with the smallest remaining processing requirement.^[24]

Service facility

• Single server: customers line up and there is only one server
• Several parallel servers–Single queue: customers line up and there are several servers
• Several servers–Several queues: there are many counters and customers can decide going where to queue

Unreliable server

Server failures occur according to a stochastic process (usually Poisson) and are followed by the setup periods during which the server is unavailable. The interrupted customer remains in the service area until server is fixed.^[25]

Customer's behavior of waiting

• Balking: customers deciding not to join the queue if it is too long
• Jockeying: customers switch between queues if they think they will get served faster by doing so
• Reneging: customers leave the queue if they have waited too long for service

Arriving customers not served (either due to the queue having no buffer, or due to balking or reneging by the customer) are also known as dropouts and the average rate of dropouts is a significant parameter describing a queue.

Queueing networks[edit]

Networks of queues are systems in which a number of queues are connected by what's known as customer routing. When a customer is serviced at one node it can join another node and queue for service, or leave the network.

For networks of m nodes, the state of the system can be described by an m–dimensional vector (x₁, x₂, ..., x_m) where x_i represents the number of customers at each node.

The simplest non-trivial network of queues is called tandem queues.^[26] The first significant results in this area were Jackson networks,^[27][28] for which an efficient product-form stationary distribution exists and the mean value analysis^[29] which allows average metrics such as throughput and sojourn times to be computed.^[30] If the total number of customers in the network remains constant the network is called a closed network and has also been shown to have a product–form stationary distribution in the Gordon–Newell theorem.^[31] This result was extended to the BCMP network^[32] where a network with very general service time, regimes and customer routing is shown to also exhibit a product-form stationary distribution. The normalizing constant can be calculated with the Buzen's algorithm, proposed in 1973.^[33]

Networks of customers have also been investigated, Kelly networks where customers of different classes experience different priority levels at different service nodes.^[34] Another type of network are G-networks first proposed by Erol Gelenbe in 1993:^[35] these networks do not assume exponential time distributions like the classic Jackson Network.

Routing algorithms[edit]

In discrete time networks where there is a constraint on which service nodes can be active at any time, the max-weight scheduling algorithm chooses a service policy to give optimal throughput in the case that each job visits only a single person ^[19] service node. In the more general case where jobs can visit more than one node, backpressure routing gives optimal throughput. A network scheduler must choose a queuing algorithm, which affects the characteristics of the larger network^{[citation needed]}. See also Stochastic scheduling for more about scheduling of queueing systems.

Mean field limits[edit]

Mean field models consider the limiting behaviour of the empirical measure (proportion of queues in different states) as the number of queues (m above) goes to infinity. The impact of other queues on any given queue in the network is approximated by a differential equation. The deterministic model converges to the same stationary distribution as the original model.^[36]

Heavy traffic/diffusion approximations[edit]

In a system with high occupancy rates (utilisation near 1) a heavy traffic approximation can be used to approximate the queueing length process by a reflected Brownian motion,^[37] Ornstein–Uhlenbeck process, or more general diffusion process.^[38] The number of dimensions of the Brownian process is equal to the number of queueing nodes, with the diffusion restricted to the non-negative orthant.

Fluid limits[edit]

Fluid models are continuous deterministic analogs of queueing networks obtained by taking the limit when the process is scaled in time and space, allowing heterogeneous objects. This scaled trajectory converges to a deterministic equation which allows the stability of the system to be proven. It is known that a queueing network can be stable, but have an unstable fluid limit.^[39]

See also[edit]

References[edit]

Further reading[edit]

• Gross, Donald; Carl M. Harris (1998). Fundamentals of Queueing Theory. Wiley. ISBN 978-0-471-32812-4. Online
• Zukerman, Moshe. Introduction to Queueing Theory and Stochastic Teletraffic Models (PDF).
• Deitel, Harvey M. (1984) [1982]. An introduction to operating systems (revisited first ed.). Addison-Wesley. p. 673. ISBN 978-0-201-14502-1. chap.15, pp. 380–412
• Newell, Gordron F. (1 June 1971). Applications of Queueing Theory. Chapman and Hall.
• Leonard Kleinrock, Information Flow in Large Communication Nets, (MIT, Cambridge, May 31, 1961) Proposal for a Ph.D. Thesis
• Leonard Kleinrock. Information Flow in Large Communication Nets(RLE Quarterly Progress Report, July 1961)
• Leonard Kleinrock. Communication Nets: Stochastic Message Flow and Delay(McGraw-Hill, New York, 1964)
• Kleinrock, Leonard (2 January 1975). Queueing Systems: Volume I – Theory. New York: Wiley Interscience. pp. 417. ISBN 978-0471491101.
• Kleinrock, Leonard (22 April 1976). Queueing Systems: Volume II – Computer Applications. New York: Wiley Interscience. pp. 576. ISBN 978-0471491118.
• Lazowska, Edward D.; John Zahorjan; G. Scott Graham; Kenneth C. Sevcik (1984). Quantitative System Performance: Computer System Analysis Using Queueing Network Models. Prentice-Hall, Inc. ISBN 978-0-13-746975-8.
• Jon Kleinberg; Éva Tardos (30 June 2013). Algorithm Design. Pearson. ISBN 978-1-292-02394-6.

External links[edit]

Look up queueing or queuing in Wiktionary, the free dictionary.

This article's use of external links may not follow Wikipedia's policies or guidelines. Please improve this article by removing excessive or inappropriate external links, and converting useful links where appropriate into footnote references. (May 2017) (Learn how and when to remove this template message)

• Queueing theory calculator
• Teknomo's Queueing theory tutorial and calculators
• Office Fire Emergency Evacuation Simulation on YouTube
• Virtamo's Queueing Theory Course
• Myron Hlynka's Queueing Theory Page
• Queueing Theory Basics
• A free online tool to solve some classical queueing systems
• JMT: an open source graphical environment for queueing theory
• LINE: a general-purpose engine to solve queueing models
• What You Hate Most About Waiting in Line: (It’s not the length of the wait.), by Seth Stevenson, Slate, 2012 – popular introduction