Модуль Верма

Модули Верма , названные в честь Дайя-Nand Верма , являются объектами в теории представлений о алгебр Ли , филиал математики .

Модули Верма можно использовать при классификации неприводимых представлений комплексной полупростой алгебры Ли. В частности, хотя сами модули Верма являются бесконечномерными, их частные можно использовать для построения конечномерных представлений с наивысшим весом , где является доминирующим и целым. ^[1] Их гомоморфизмы соответствуют инвариантным дифференциальным операторам над многообразиями флагов .${\ displaystyle \ lambda}$${\ displaystyle \ lambda}$

Неформальное строительство [ править ]

Вес модуля Верма с наибольшим весом ${\ displaystyle \ lambda}$

Мы можем объяснить идею модуля Верма следующим образом. ^[2] Позвольте быть полупростой алгеброй Ли (над , для простоты). Позвольте быть фиксированной подалгеброй Картана в и пусть быть ассоциированной корневой системой. Позвольте быть фиксированным набором положительных корней. Для каждого выберите ненулевой элемент для соответствующего корневого пространства и ненулевой элемент в корневом пространстве . Мы думаем о 'как о «операторах повышения», а ' s как о «операторах опускания».${\ displaystyle {\ mathfrak {g}}}$${\ displaystyle \ mathbb {C}}$${\ displaystyle {\ mathfrak {h}}}$${\ displaystyle {\ mathfrak {g}}}$${\ displaystyle R}$${\ Displaystyle R ^ {+}}$${\ Displaystyle \ альфа \ в R ^ {+}}$${\ displaystyle X _ {\ alpha}}$${\ displaystyle {\ mathfrak {g}} _ {\ alpha}}$${\ displaystyle Y _ {\ alpha}}$${\ displaystyle {\ mathfrak {g}} _ {- \ alpha}}$${\ displaystyle X _ {\ alpha}}$${\ displaystyle Y _ {\ alpha}}$

Теперь позвольте быть произвольным линейным функционалом, не обязательно доминирующим или целым. Наша цель состоит в том, чтобы построить представление о с высоким весом , который генерируется один ненулевой вектор с весом . Модуль Верма является одним из таких модулей со старшим весом, который является максимальным в том смысле, что любой другой модуль со старшим весом является частным по отношению к модулю Верма. Оказывается, модули Верма всегда бесконечномерны; если - доминантный интеграл, однако можно построить конечномерный фактормодуль модуля Верма. Таким образом, модули Верма играют важную роль в классификации конечномерных представлений о${\displaystyle \lambda \in {\mathfrak {h}}^{*}}$${\displaystyle W_{\lambda }}$${\displaystyle {\mathfrak {g}}}$${\displaystyle \lambda }$${\displaystyle v}$${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle {\mathfrak {g}}}$. В частности, они являются важным инструментом в жесткой части теоремы о наивысшем весе, а именно, показывая, что каждый доминирующий интегральный элемент на самом деле возникает как наивысший вес конечномерного неприводимого представления .${\displaystyle {\mathfrak {g}}}$

Теперь мы пытаемся интуитивно понять, как должен выглядеть модуль Verma с наибольшим весом . Поскольку должен быть вектором с наибольшим весом с весом , мы определенно хотим ${\displaystyle \lambda }$${\displaystyle v}$${\displaystyle \lambda }$

${\displaystyle H\cdot v=\lambda (H)v,\quad H\in {\mathfrak {h}}}$

а также

${\displaystyle X_{\alpha }\cdot v=0,\quad \alpha \in R^{+}}$.

Затем должны быть охвачены элементы, полученные путем понижения под действием 's:${\displaystyle W_{\lambda }}$${\displaystyle v}$${\displaystyle Y_{\alpha }}$

${\displaystyle Y_{\alpha _{i_{1}}}\cdots Y_{\alpha _{i_{M}}}\cdot v}$.

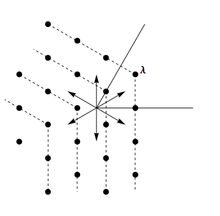
Теперь мы устанавливаем только те отношения между векторами указанного выше вида, которые требуются коммутационными отношениями между 's. В частности, модуль Верма всегда бесконечномерен. Веса модуля Верма с наивысшим весом будут состоять из всех элементов, которые могут быть получены путем вычитания целочисленных комбинаций положительных корней. На рисунке показаны веса модуля Верма для .${\displaystyle Y}$${\displaystyle \lambda }$${\displaystyle \mu }$${\displaystyle \lambda }$${\displaystyle \mathrm {sl} (3;\mathbb {C} )}$

Простой аргумент переупорядочения показывает, что есть только один возможный способ действия полной алгебры Ли на этом пространстве. В частности, если есть любой элемент из , то по простой части теоремы Пуанкаре – Биркгофа – Витта мы можем переписать${\displaystyle {\mathfrak {g}}}$${\displaystyle Z}$${\displaystyle {\mathfrak {g}}}$

${\displaystyle ZY_{\alpha _{i_{1}}}\cdots Y_{\alpha _{i_{M}}}}$

как линейная комбинация произведений элементов алгебры Ли с повышающими операторами, действующими первыми, элементами подалгебры Картана и, наконец, понижающими операторами . Применяя эту сумму членов к , любой член с оператором возведения равен нулю, любые множители в Картане действуют как скаляры, и, таким образом, мы получаем элемент исходной формы.${\displaystyle X_{\alpha }}$${\displaystyle Y_{\alpha }}$${\displaystyle v}$

Чтобы лучше понять структуру модуля Верма, мы можем выбрать порядок положительных корней как и позволить соответствующим операторам понижения на . Затем с помощью простого аргумента переупорядочения каждый элемент приведенной выше формы может быть переписан как линейная комбинация элементов с 's в определенном порядке:${\displaystyle \alpha _{1},\ldots \alpha _{n}}$${\displaystyle Y_{1},\ldots Y_{n}}$${\displaystyle Y}$

${\displaystyle Y_{1}^{k_{1}}\cdots Y_{n}^{k_{n}}v}$,

где неотрицательные целые числа. Собственно оказывается, что такие векторы составляют основу модуля Верма.${\displaystyle k_{j}}$

Хотя это описание модуля Верма дает интуитивное представление о том, как он выглядит, все же остается дать его строгое построение. В любом случае модуль Верма дает - для любого , не обязательно доминирующего или интегрального - представление с наивысшим весом . Цена, которую мы платим за эту относительно простую конструкцию, всегда бесконечна. В случае доминирующего и целого можно построить конечномерный неприводимый фактор модуля Верма. ^[3]${\displaystyle W_{\lambda }}$ ${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle W_{\lambda }}$${\displaystyle \lambda }$

Случай ${\displaystyle \mathrm {sl} (2;\mathbb {C} )}$[ править ]

Пусть будет обычным основанием для :${\displaystyle {X,Y,H}}$${\displaystyle \mathrm {sl} (2;\mathbb {C} )}$

${\displaystyle X={\begin{pmatrix}0&1\\0&0\end{pmatrix}}\qquad Y={\begin{pmatrix}0&0\\1&0\end{pmatrix}}\qquad H={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}~,}$

с подалгеброй Картана, являющейся оболочкой . Позвольте быть определено для произвольного комплексного числа . Тогда модуль Верма со старшим весом натянут на линейно независимые векторы, и действие базисных элементов будет следующим: ^[4]${\displaystyle H}$${\displaystyle \lambda }$${\displaystyle \lambda (H)=m}$${\displaystyle m}$${\displaystyle \lambda }$${\displaystyle v_{0},v_{1},v_{2},\dots }$

${\displaystyle Y\cdot v_{j}=v_{j+1};\quad X\cdot v_{j}=j(m-(j-1))v_{j-1};\quad H\cdot v_{j}=(m-2j)v_{j}}$.

(Это означает, в частности, то и то .) Эти формулы основаны на том, как базисные элементы действуют в конечномерных представлениях , за исключением того, что мы больше не требуем, чтобы "цепочка" собственных векторов для должна завершаться.${\displaystyle H\cdot v_{0}=mv_{0}}$${\displaystyle X\cdot v_{0}=0}$${\displaystyle \mathrm {sl} (2;\mathbb {C} )}$${\displaystyle H}$

В этой конструкции - произвольное комплексное число, не обязательно действительное, положительное или целое. Тем не менее, случай, когда - целое неотрицательное число, особенный. В этом случае легко увидеть , что промежуток векторов инвариантен - потому что . Фактормодуль тогда является конечномерным неприводимым представлением размерности${\displaystyle m}$${\displaystyle m}$${\displaystyle v_{m+1},v_{m+2},\ldots }$${\displaystyle X\cdot v_{m+1}=0}$${\displaystyle \mathrm {sl} (2;\mathbb {C} )}$${\displaystyle m+1.}$

Определение модулей Verma [ править ]

Есть две стандартные конструкции модуля Верма, каждая из которых включает концепцию универсальной обертывающей алгебры . Мы продолжаем обозначения предыдущего раздела: является комплексной полупростой алгеброй Ли, является фиксированной подалгеброй Картана, является ассоциированной корневой системой с фиксированным набором положительных корней. Для каждого выберем ненулевые элементы и .${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak {h}}}$${\displaystyle R}$${\displaystyle R^{+}}$${\displaystyle \alpha \in R^{+}}$${\displaystyle X_{\alpha }\in {\mathfrak {g}}_{\alpha }}$${\displaystyle Y_{\alpha }\in {\mathfrak {g}}_{-\alpha }}$

Как частное от обертывающей алгебры [ править ]

Первая конструкция ^[5] модуля Верма является фактором универсальной обертывающей в . Поскольку предполагается, что модуль Верма является -модулем, он также будет -модулем в силу универсального свойства обертывающей алгебры. Таким образом, если у нас есть модуль Верма с вектором старшего веса , будет линейное отображение из в, заданное формулой${\displaystyle U({\mathfrak {g}})}$${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle U({\mathfrak {g}})}$${\displaystyle W_{\lambda }}$${\displaystyle v}$${\displaystyle \Phi }$${\displaystyle U({\mathfrak {g}})}$${\displaystyle W_{\lambda }}$

${\displaystyle \Phi (x)=x\cdot v,\quad x\in U({\mathfrak {g}})}$.

Поскольку предполагается, что он порождается , карта должна быть сюръективной. Поскольку предполагается, что это вектор с наивысшим весом, ядро должно включать все корневые векторы для in . Поскольку также предполагается, что это весовой вектор с весом , ядро должно включать все векторы вида${\displaystyle W_{\lambda }}$${\displaystyle v}$${\displaystyle \Phi }$${\displaystyle v}$${\displaystyle \Phi }$${\displaystyle X_{\alpha }}$${\displaystyle \alpha }$${\displaystyle R^{+}}$${\displaystyle v}$${\displaystyle \lambda }$${\displaystyle \Phi }$

${\displaystyle H-\lambda (H)1,\quad H\in {\mathfrak {h}}}$.

Наконец, ядро должно быть левым идеалом в ; в конце концов, если то для всех .${\displaystyle \Phi }$${\displaystyle U({\mathfrak {g}})}$${\displaystyle x\cdot v=0}$${\displaystyle (yx)\cdot v=y\cdot (x\cdot v)=0}$${\displaystyle y\in U({\mathfrak {g}})}$

Предыдущее обсуждение мотивирует следующую конструкцию модуля Верма. Мы определяем как фактор-векторное пространство${\displaystyle W_{\lambda }}$

${\displaystyle W_{\lambda }=U({\mathfrak {g}})/I_{\lambda }}$,

где левый идеал порожден всеми элементами вида ${\displaystyle I_{\lambda }}$

${\displaystyle X_{\alpha },\quad \alpha \in R^{+},}$

а также

${\displaystyle H-\lambda (H)1,\quad H\in {\mathfrak {h}}}$.

Поскольку является левым идеалом, естественное левое действие элемента на себя переносится на частное. Таким образом, является -модулем, а значит, и -модулем.${\displaystyle I_{\lambda }}$${\displaystyle U({\mathfrak {g}})}$${\displaystyle W_{\lambda }}$${\displaystyle U({\mathfrak {g}})}$${\displaystyle {\mathfrak {g}}}$

Расширением скаляров [ править ]

Процедура « расширения скаляров » - это метод замены левого модуля над одной алгеброй (не обязательно коммутативным) в левый модуль над большей алгеброй, которая содержит в качестве подалгебры. Мы можем рассматривать его как правый -модуль, где действует умножением справа. Поскольку является левым -модулем и правым -модулем, мы можем сформировать тензорное произведение двух над алгеброй :${\displaystyle V}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle V}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle A_{1}}$

${\displaystyle A_{2}\otimes _{A_{1}}V}$.

Теперь, поскольку является левым -модулем над собой, указанное выше тензорное произведение несет структуру левого модуля над большей алгеброй , однозначно определяемую требованием, чтобы${\displaystyle A_{2}}$${\displaystyle A_{2}}$${\displaystyle A_{2}}$

${\displaystyle a_{1}\cdot (a_{2}\otimes v)=(a_{1}a_{2})\otimes v}$

для всех и в . Таким образом, начиная с левого -модуля , мы получили левый -модуль .${\displaystyle a_{1}}$${\displaystyle a_{2}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle V}$${\displaystyle A_{2}}$${\displaystyle A_{2}\otimes _{A_{1}}V}$

Теперь применим эту конструкцию к полупростой алгебре Ли. Мы выпускаем подалгебра натянутое и корневых векторов с . (Таким образом, это "борелевская подалгебра" .) Мы можем сформировать левый модуль над универсальной обертывающей алгеброй следующим образом:${\displaystyle {\mathfrak {b}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak {h}}}$${\displaystyle X_{\alpha }}$${\displaystyle \alpha \in R^{+}}$${\displaystyle {\mathfrak {b}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle F_{\lambda }}$${\displaystyle U({\mathfrak {b}})}$

• ${\displaystyle F_{\lambda }}$это один-мерное векторное пространство , натянутое на одном векторе вместе с - модуль структуры таким образом, что действует как умножение на и положительные корневые пространства действуют тривиально:${\displaystyle v}$${\displaystyle {\mathfrak {b}}}$${\displaystyle {\mathfrak {h}}}$${\displaystyle \lambda }$

${\displaystyle \quad H\cdot v=\lambda (H)v,\quad H\in {\mathfrak {h}};\quad X_{\alpha }\cdot v=0,\quad \alpha \in R^{+}}$.

Мотивация для этой формулы заключается в том, что она описывает, как предполагается действовать на вектор наивысшего веса в модуле Верма.${\displaystyle U({\mathfrak {b}})}$

Теперь из теоремы Пуанкаре – Биркгофа – Витта следует, что является подалгеброй в . Таким образом, мы можем применить расширение техники скаляров для преобразования левого -модуля в левый -модуль следующим образом:${\displaystyle U({\mathfrak {b}})}$${\displaystyle U({\mathfrak {g}})}$${\displaystyle F_{\lambda }}$${\displaystyle U({\mathfrak {b}})}$${\displaystyle U({\mathfrak {g}})}$${\displaystyle W_{\lambda }}$

${\displaystyle W_{\lambda }:=U({\mathfrak {g}})\otimes _{U({\mathfrak {b}})}F_{\lambda }}$.

Поскольку является левым -модулем, он, в частности, является модулем (представлением) для .${\displaystyle W_{\lambda }}$${\displaystyle U({\mathfrak {g}})}$${\displaystyle {\mathfrak {g}}}$

Структура модуля Верма [ править ]

Какую бы конструкцию модуля Верма ни использовали, нужно доказать, что он нетривиален, т. Е. Не нулевой модуль. На самом деле, можно использовать теорему Пуанкаре – Биркгофа – Витта, чтобы показать, что лежащее в основе векторное пространство изоморфно${\displaystyle W_{\lambda }}$

${\displaystyle U({\mathfrak {g}}_{-})}$

где - подалгебра Ли, порожденная отрицательными корневыми пространствами (то есть 's). ^[6]${\displaystyle {\mathfrak {g}}_{-}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle Y_{\alpha }}$

Основные свойства [ править ]

Модули Верма, рассматриваемые как - модули , являются модулями старшего веса , т. Е. Они порождаются вектором старшего веса . Этот вектор наивысшего веса (первый - это единица измерения, а второй - это единица поля , рассматриваемый как - модуль ), и он имеет вес .${\displaystyle {\mathfrak {g}}}$${\displaystyle 1\otimes 1}$${\displaystyle 1}$${\displaystyle {\mathcal {U}}({\mathfrak {g}})}$${\displaystyle F}$${\displaystyle {\mathfrak {b}}}$${\displaystyle F_{\lambda }}$${\displaystyle \lambda }$

Кратности [ править ]

Модули Верма являются весовыми модулями , т.е. представляют собой прямую сумму всех своих весовых пространств . Каждое весовое пространство в конечномерно, а размерность -весового пространства - это количество способов выражения в виде суммы положительных корней (это тесно связано с так называемой статистической суммой Костанта ). Это утверждение следует из предыдущего утверждения, что модуль Верма изоморфен как векторное пространство , наряду с теоремой Пуанкаре – Биркгофа – Витта для .${\displaystyle W_{\lambda }}$${\displaystyle W_{\lambda }}$${\displaystyle \mu }$${\displaystyle W_{\mu }}$${\displaystyle \lambda -\mu }$${\displaystyle U({\mathfrak {g}}_{-})}$${\displaystyle U({\mathfrak {g}}_{-})}$

Универсальное свойство [ править ]

Модули Верма имеют очень важное свойство: если любое представление , порожденное старшим вектором веса , есть сюръективны - гомоморфизм То есть, все представления с наибольшим весом , которые порождаются вектором старшего веса (так называемые высокие модули веса ) являются частными от${\displaystyle V}$${\displaystyle \lambda }$ ${\displaystyle {\mathfrak {g}}}$ ${\displaystyle W_{\lambda }\to V.}$${\displaystyle \lambda }$${\displaystyle W_{\lambda }.}$

Модуль неприводимого частного [ править ]

${\displaystyle W_{\lambda }}$содержит единственный максимальный подмодуль , а его фактор - единственное (с точностью до изоморфизма ) неприводимое представление со старшим весом ^[7]. Если старший вес является доминантным и целым, то доказывается, что этот неприводимый фактор действительно конечномерен. ^[8]${\displaystyle \lambda .}$${\displaystyle \lambda }$

В качестве примера рассмотрим рассмотренный выше случай . Если наивысший вес - это «доминирующий интеграл», то есть просто неотрицательное целое число, тогда диапазон элементов остается неизменным. Тогда фактор-представление неприводимо с размерностью . Фактор-представление натянуто на линейно независимые векторы . Действие такое же, как в модуле Верма, за исключением того, что в частном по сравнению с модулем Верма.${\displaystyle {\mathfrak {g}}=\operatorname {sl} (2;\mathbb {C} )}$${\displaystyle m}$${\displaystyle Xv_{m+1}=0}$${\displaystyle v_{m+1},v_{m+2},\ldots }$${\displaystyle m+1}$${\displaystyle v_{0},v_{1},\ldots ,v_{m}}$${\displaystyle \operatorname {sl} (2;\mathbb {C} )}$${\displaystyle Yv_{m}=0}$${\displaystyle Yv_{m}=v_{m+1}}$

Сам модуль Верма неприводим тогда и только тогда, когда ни одна из координат в базисе фундаментальных весов не принадлежит множеству .${\displaystyle W_{\lambda }}$${\displaystyle \lambda }$${\displaystyle \{0,1,2,\ldots \}}$

Другие свойства [ править ]

Модуль Верма называется регулярным , если его старший вес λ лежит на аффинной орбите Вейля доминантного веса . Другими словами, существует такой элемент w группы Вейля W, что${\displaystyle W_{\lambda }}$${\displaystyle {\tilde {\lambda }}}$

${\displaystyle \lambda =w\cdot {\tilde {\lambda }}}$

где - аффинное действие группы Вейля .${\displaystyle \cdot }$

Модуль Верма называется сингулярным , если на аффинной орбите λ нет доминирующего веса. В этом случае существует вес, который находится на стенке фундаментальной камеры Вейля (δ - это сумма всех основных весов ).${\displaystyle W_{\lambda }}$${\displaystyle {\tilde {\lambda }}}$${\displaystyle {\tilde {\lambda }}+\delta }$

Гомоморфизмы модулей Верма [ править ]

Для любых двух весов нетривиальный гомоморфизм${\displaystyle \lambda ,\mu }$

${\displaystyle W_{\mu }\rightarrow W_{\lambda }}$

может существовать, только если и связаны с аффинным действием группы Вейля алгебры Ли . Это легко следует из теоремы Хариш-Чандры о бесконечно малых центральных характерах .${\displaystyle \mu }$${\displaystyle \lambda }$ ${\displaystyle W}$${\displaystyle {\mathfrak {g}}}$

Каждый гомоморфизм модулей Верма инъективен и размерность

${\displaystyle \dim(\operatorname {Hom} (W_{\mu },W_{\lambda }))\leq 1}$

для любого . Итак, ненулевой существует тогда и только тогда, когда он изоморфен (уникальному) подмодулю модуля .${\displaystyle \mu ,\lambda }$${\displaystyle W_{\mu }\rightarrow W_{\lambda }}$${\displaystyle W_{\mu }}$${\displaystyle W_{\lambda }}$

Полная классификация гомоморфизмов модулей Верма была проведена Бернштейном – Гельфандом – Гельфандом ^[9] и Верма ^[10] и может быть резюмирована в следующем утверждении:

Ненулевой гомоморфизм существует тогда и только тогда, когда существует ${\displaystyle W_{\mu }\rightarrow W_{\lambda }}$

последовательность весов

${\displaystyle \mu =\nu _{0}\leq \nu _{1}\leq \ldots \leq \nu _{k}=\lambda }$

таким образом, что для некоторых положительных корней (и является соответствующим корнем отражения и является суммой всех основных весов ) и для каждого является натуральным числом ( это кокорень связан с корнем ).${\displaystyle \nu _{i-1}+\delta =s_{\gamma _{i}}(\nu _{i}+\delta )}$${\displaystyle \gamma _{i}}$${\displaystyle s_{\gamma _{i}}}$${\displaystyle \delta }$${\displaystyle 1\leq i\leq k,(\nu _{i}+\delta )(H_{\gamma _{i}})}$${\displaystyle H_{\gamma _{i}}}$${\displaystyle \gamma _{i}}$

Если модули Вермы и являются регулярными , то существует единственный доминантный вес и уникальные элементы ш , ш 'из группы Вейля W таким образом, что${\displaystyle M_{\mu }}$${\displaystyle M_{\lambda }}$ ${\displaystyle {\tilde {\lambda }}}$

${\displaystyle \mu =w'\cdot {\tilde {\lambda }}}$

а также

${\displaystyle \lambda =w\cdot {\tilde {\lambda }},}$

где - аффинное действие группы Вейля. Если веса далее целые , то существует ненулевой гомоморфизм${\displaystyle \cdot }$

${\displaystyle W_{\mu }\to W_{\lambda }}$

если и только если

${\displaystyle w\leq w'}$

в порядке Брюа группы Вейля.

Серия Джордана – Гёльдера [ править ]

Позволять

${\displaystyle 0\subset A\subset B\subset W_{\lambda }}$

последовательность -модулей, так что фактор-модуль B / A неприводим со старшим весом μ. Тогда существует ненулевой гомоморфизм .${\displaystyle {\mathfrak {g}}}$${\displaystyle W_{\mu }\to W_{\lambda }}$

Легким следствием этого является то, что для любых модулей старшего веса, таких что${\displaystyle V_{\mu },V_{\lambda }}$

${\displaystyle V_{\mu }\subset V_{\lambda }}$

существует ненулевой гомоморфизм .${\displaystyle W_{\mu }\to W_{\lambda }}$

Резолюция Бернштейна – Гельфанда – Гельфанда [ править ]

Пусть будет конечномерным неприводимым представлением в алгебре Ли с старшим весом Х. Из раздела о гомоморфизмах модулей Верма мы знаем, что существует гомоморфизм${\displaystyle V_{\lambda }}$ ${\displaystyle {\mathfrak {g}}}$

${\displaystyle W_{w'\cdot \lambda }\to W_{w\cdot \lambda }}$

если и только если

${\displaystyle w\leq w'}$

в порядке Брюа группы Вейля . Следующая теорема описывает решение о в терминах модулей Верма (это было доказано Бернштейна - Гельфанда - Гельфанд в 1975 г. ^[11] ):${\displaystyle V_{\lambda }}$

Существует точная последовательность -гомоморфизмов${\displaystyle {\mathfrak {g}}}$

${\displaystyle 0\to \oplus _{w\in W,\,\,\ell (w)=n}W_{w\cdot \lambda }\to \cdots \to \oplus _{w\in W,\,\,\ell (w)=2}W_{w\cdot \lambda }\to \oplus _{w\in W,\,\,\ell (w)=1}W_{w\cdot \lambda }\to W_{\lambda }\to V_{\lambda }\to 0}$

где n - длина наибольшего элемента группы Вейля.

Аналогичное разрешение существует и для обобщенных модулей Верма . Кратко обозначается как разрешение BGG .

См. Также [ править ]

• Классификация конечномерных представлений алгебр Ли
• Теорема старшего веса
• Обобщенный модуль Верма
• Модуль Вейля

Заметки [ править ]

Ссылки [ править ]

• Bäuerle, GGA; де Керф, EA; тен Кроуд, APE (1997). А. ван Грезен; Э. М. де Ягер (ред.). Конечномерные и бесконечномерные алгебры Ли и их применение в физике . Исследования по математической физике. 7 . Северная Голландия. Глава 20. ISBN 978-0-444-82836-1- через ScienceDirect .
• Картер Р. (2005), Алгебры Ли конечного и аффинного типа , Cambridge University Press, ISBN 978-0-521-85138-1.
• Диксмье, Дж. (1977), Обертывающие алгебры , Амстердам, Нью-Йорк, Оксфорд: Северная Голландия, ISBN 978-0-444-11077-0.
• Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для выпускников по математике, 222 (2-е изд.), Springer, ISBN 978-3319134666
• Хамфрис, Дж. (1980), Введение в алгебры Ли и теорию представлений , Springer Verlag, ISBN 978-3-540-90052-8.
• Кнапп, А.В. (2002), Группы Ли за пределами введения (2-е изд.), Биркхойзер, стр. 285, ISBN 978-0-8176-3926-6.
• Роча, Алвани (2001) [1994], "Разрешение BGG" , Энциклопедия математики , EMS Press CS1 maint: discouraged parameter (link)
• Roggenkamp, ​​K .; Стефанеску, М. (2002), Алгебра - теория представлений , Springer, ISBN 978-0-7923-7114-4.

Эта статья включает материал из модуля Verma на PlanetMath , который находится под лицензией Creative Commons Attribution / Share-Alike License .