Алгоритм Ллойда

Пример алгоритма Ллойда. Показана диаграмма Вороного текущих точек на каждой итерации. Знаки плюс обозначают центроиды ячеек Вороного.

Итерация 2

Итерация 3

Итерация 15

На последнем изображении точки находятся очень близко к центроидам ячеек Вороного. Обнаружена центроидная мозаика Вороного.

В области электротехники и информатики , алгоритм Ллойда , также известный как Вороного итерации или релаксации, является алгоритм имени Стюарт П. Ллойда для нахождения равномерно разнесенных множества точек в подмножеств евклидовых пространств и перегородок этих подмножеств в стройные и равномерно размер выпуклых ячеек. ^[1] Подобно тесно связанному алгоритму кластеризации k- средних , он неоднократно находит центроидкаждого набора в разделе, а затем повторно разбивает входные данные в соответствии с тем, какой из этих центроидов является ближайшим. В этой настройке средняя операция представляет собой интеграл по области пространства, а операция ближайшего центроида приводит к диаграммам Вороного .

Хотя алгоритм может быть применен непосредственно к евклидовой плоскости , аналогичные алгоритмы могут также применяться к пространствам более высокой размерности или к пространствам с другими неевклидовыми метриками. Алгоритм Ллойда можно использовать для построения близких приближений к центроидным мозаикам Вороного входных данных ^[2], которые можно использовать для квантования , сглаживания и штриховки . Другие применения алгоритма Ллойда включают сглаживание треугольных сеток в методе конечных элементов .

История [ править ]

Алгоритм был впервые предложен Стюартом П. Ллойдом из Bell Labs в 1957 году как метод импульсно-кодовой модуляции . Работа Ллойда получила широкое распространение, но оставалась неопубликованной до 1982 года. ^[1] Подобный алгоритм был независимо разработан Джоэлом Максом и опубликован в 1960 году ^[3], поэтому алгоритм иногда называют алгоритмом Ллойда-Макса.

Описание алгоритма [ править ]

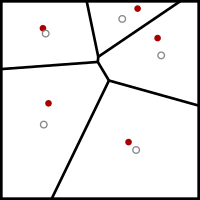
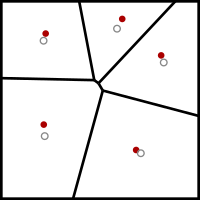
Алгоритм Ллойда начинается с первоначального размещения некоторого количества k точечных сайтов во входном домене. В приложениях для сглаживания сетки это будут вершины сетки, которую нужно сгладить; в других приложениях они могут быть размещены произвольно или путем пересечения однородной треугольной сетки соответствующего размера с входной областью.

Затем он повторно выполняет следующий шаг релаксации:

• Диаграмма Вороного из K сайтов вычисляется.
• Каждая ячейка диаграммы Вороного интегрируется, и вычисляется центроид.
• Затем каждый сайт перемещается в центр тяжести своей ячейки Вороного.

Интеграция и вычисление центроидов [ править ]

Поскольку алгоритмы построения диаграммы Вороного могут быть в высшей степени нетривиальными, особенно для входных данных размерностью более двух, шаги вычисления этой диаграммы и нахождения точных центроидов ее ячеек могут быть заменены приближением.

Приближение [ править ]

Обычным упрощением является использование подходящей дискретизации пространства, такой как мелкая пиксельная сетка, например, буфер текстуры в графическом оборудовании. Ячейки материализуются в виде пикселей, помеченных соответствующим идентификатором сайта. Новый центр ячейки аппроксимируется путем усреднения положений всех пикселей, которым присвоены одинаковые метки. В качестве альтернативы можно использовать методы Монте-Карло , в которых случайные точки выборки генерируются согласно некоторому фиксированному базовому распределению вероятностей, назначаются ближайшему участку и усредняются для аппроксимации центроида для каждого участка.

Точное вычисление [ править ]

Хотя вложения в других пространствах также возможно, эта разработка предполагает евклидово пространство с помощью L ² нормы и рассматриваются два наиболее соответствующие сценарии, которые два, и , соответственно , три измерения.

Поскольку клетка Вороного имеет выпуклую форму и всегда охватывает ее узел, существуют тривиальные разложения на легко интегрируемые симплексы:

• В двух измерениях края многоугольной ячейки соединяются с ее участком, образуя набор треугольников в форме зонтика.
• В трех измерениях ячейка окружена несколькими плоскими многоугольниками, которые сначала необходимо триангулировать:
  • Вычислите центр грани многоугольника, например, среднее значение всех его вершин.
  • Соединение вершин многоугольника с его центром дает плоскую триангуляцию в форме зонтика.
  • Тривиально набор тетраэдров получается соединением треугольников корпуса ячейки с местом ячейки.

Интегрирование ячейки и вычисление ее центроида (центра масс) теперь дается как взвешенная комбинация центроидов ее симплексов (далее называемых ).${\ textstyle \ mathbf {c} _ {я}}$

• Два измерения:
  • Центроид треугольника можно легко вычислить, например, используя декартовы координаты .
  • Взвешивание рассчитывается как отношение площади симплекса к площади ячейки .
• Три измерения:
  • Центроид тетраэдра находится как пересечение трех плоскостей биссекторной и может быть выражена в виде матрицы на вектор.
  • Взвешивание рассчитывается как отношение объема симплекса к объему ячейки .

Для двумерной ячейки с n треугольными симплексами и накопленной площадью (где - площадь симплекса треугольника ) новый центроид ячейки вычисляется как:${\ textstyle A_ {C} = \ sum _ {i = 0} ^ {n} a_ {i}}$${\ textstyle a_ {i}}$

${\ displaystyle C = {\ frac {1} {A_ {C}}} \ sum _ {i = 0} ^ {n} \ mathbf {c} _ {i} a_ {i}}$

Аналогично, для трехмерной ячейки с объемом (где - объем симплекса тетраэдра ) центроид вычисляется как:${\textstyle V_{C}=\sum _{i=0}^{n}v_{i}}$${\textstyle v_{i}}$

${\displaystyle C={\frac {1}{V_{C}}}\sum _{i=0}^{n}\mathbf {c} _{i}v_{i}}$

Конвергенция [ править ]

Каждый раз, когда выполняется шаг релаксации, точки остаются в немного более равномерном распределении: близко расположенные точки перемещаются дальше друг от друга, а широко разнесенные точки перемещаются ближе друг к другу. Было показано, что в одном измерении этот алгоритм сходится к центроидной диаграмме Вороного, также называемой центроидной тесселяцией Вороного . ^[4] В более высоких измерениях известны несколько более слабые результаты сходимости. ^{[5] [6]}

Алгоритм сходится медленно или из-за ограничений числовой точности может не сходиться. Следовательно, реальное применение алгоритма Ллойда обычно останавливается, когда распределение «достаточно хорошее». Одним из общих критериев завершения является остановка, когда максимальное расстояние, на которое перемещается любой сайт за итерацию, становится ниже заранее установленного порога. Сходимость может быть ускорена за счет чрезмерного расслабления точек, что достигается перемещением каждой точки ω, умноженной на расстояние до центра масс, обычно с использованием значения чуть меньше 2 для ω . ^[7]

Приложения [ править ]

Метод Ллойда первоначально использовался для скалярного квантования, но ясно, что этот метод распространяется также и на векторное квантование. Таким образом, он широко используется в методах сжатия данных в теории информации . Метод Ллойда используется в компьютерной графике, поскольку полученное распределение имеет характеристики синего шума (см. Также « Цвета шума» ), что означает, что существует несколько низкочастотных компонентов, которые можно интерпретировать как артефакты. Он особенно хорошо подходит для выбора позиций сэмпла для дизеринга . Алгоритм Ллойда также используется для создания точечных рисунков в стиле штриховки . ^[8]В этом приложении центроиды могут быть взвешены на основе эталонного изображения для создания точечных иллюстраций, соответствующих входному изображению. ^[9]

В методе конечных элементов входная область сложной геометрии разбивается на элементы более простой формы; например, двумерные области (либо подмножества евклидовой плоскости, либо трехмерные поверхности) часто делятся на треугольники. Для сходимости методов конечных элементов важно, чтобы эти элементы имели правильную форму; в случае треугольников предпочтение отдается элементам, которые почти равносторонние треугольники. Алгоритм Ллойда можно использовать для сглаживания сетки, созданной каким-либо другим алгоритмом, перемещая ее вершины и изменяя схему соединения между ее элементами, чтобы создавать треугольники, которые более точно равносторонние. ^[10]Эти приложения обычно используют меньшее количество итераций алгоритма Ллойда, останавливая его до сходимости, чтобы сохранить другие особенности сетки, такие как различия в размерах элементов в разных частях сетки. В отличие от другого метода сглаживания, лапласовского сглаживания (при котором вершины сетки перемещаются в среднее положение их соседей), алгоритм Ллойда может изменять топологию сетки, приводя к более близким к равносторонним элементам, а также избегая проблем с запутывание, которое может возникнуть при лапласовском сглаживании. Однако лапласовское сглаживание может применяться в более общем смысле к сеткам с нетреугольными элементами.

Разные расстояния [ править ]

Алгоритм Ллойда обычно используется в евклидовом пространстве . Евклидово расстояние играет в алгоритме две роли: оно используется для определения ячеек Вороного, но оно также соответствует выбору центроида в качестве репрезентативной точки каждой ячейки, поскольку центроид - это точка, которая минимизирует средний квадрат евклидова расстояния. к точкам в своей ячейке. Вместо этого могут использоваться альтернативные расстояния и альтернативные центральные точки, чем центроид. Например, Хауснер (2001) использовал вариант манхэттенской метрики (с локально изменяющейся ориентацией), чтобы найти мозаичное покрытие изображения приблизительно квадратными плитками, ориентация которых совпадает с особенностями изображения, которые он использовал для моделирования построения мозаики из плиток. .^[11] В этом приложении, несмотря на изменение метрики, Хауснер продолжал использовать центроиды в качестве репрезентативных точек своих ячеек Вороного. Однако для показателей, которые более существенно отличаются от евклидовых, может оказаться целесообразным выбрать в качестве репрезентативной точки минимизатор среднего квадрата расстояния вместо центроида. ^[12]

См. Также [ править ]

• Алгоритм Linde-Бузо-серый , обобщение этого алгоритма векторного квантования
• Обход от начала до конца , другой метод создания равномерно распределенных точек в геометрических пространствах.
• Среднее смещение , родственный метод нахождения максимумов функции плотности
• K-означает ++

Ссылки [ править ]

Внешние ссылки [ править ]

• DemoGNG.js Графический симулятор Javascript для алгоритма LBG и других моделей, включает отображение областей Вороного