Аффинное масштабирование

Метод аффинного масштабирования - это метод внутренней точки , то есть он формирует траекторию точек строго внутри допустимой области линейной программы (в отличие от симплексного алгоритма , который проходит по углам допустимой области).

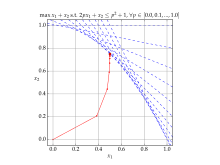
В математической оптимизации , аффинная масштабирования является алгоритм для решения линейного программирования задач. В частности, это метод внутренней точки , открытый советским математиком И.И. Дикиным в 1967 году и заново изобретенный в США в середине 1980-х годов.

История [ править ]

Аффинное масштабирование имеет историю множественных открытий . Впервые он был опубликован И.И. Дикиным в Институте энергетических систем Российской академии наук (в то время Сибирский энергетический институт АН СССР) в Докладе Академии наук СССР за 1967 год , после чего в 1974 году последовало доказательство его сходимости ^{[1]. ]} Работа Дикина оставалась практически незамеченной до открытия в 1984 г. алгоритма Кармаркара , первого практического алгоритма с полиномиальным временем для линейного программирования. Важность и сложность метода Кармаркара побудили математиков искать более простой вариант.

Затем несколько групп независимо друг от друга разработали вариант алгоритма Кармаркара. ЭР Барнс в IBM , ^[2] команда во главе с RJ Vanderbei на AT & T , ^[3] и некоторые других заменили проективные преобразования , которые Кармаркар , используемый аффинных из них. Спустя несколько лет стало понятно, что «новые» алгоритмы аффинного масштабирования на самом деле являются переосмыслением результатов Дикина, полученных десятилетней давности. ^[1]^[4] Из открывателей только Барнс и Вандербей и др.удалось провести анализ свойств сходимости аффинного масштабирования. Кармаркар, который также использовал аффинное масштабирование в этот период времени, ошибочно полагал, что оно сходится так же быстро, как его собственный алгоритм. ^[5]^{: 346}

Алгоритм [ править ]

Аффинное масштабирование работает в два этапа, первая из которых определяет возможную точку, с которой можно начать оптимизацию, а вторая выполняет фактическую оптимизацию, оставаясь строго внутри допустимой области.

Обе фазы решают линейные программы в форме равенства, а именно.

минимизировать

c \cdot x

при условии

Ax = b

,

x \geq 0

.

Эти проблемы решаются с помощью итеративного метода , который концептуально продолжается путем построения траектории точек строго внутри допустимой области проблемы, вычисления запланированных шагов градиентного спуска в масштабированной версии задачи, а затем масштабирования шага обратно к исходному проблема. Масштабирование гарантирует, что алгоритм может продолжать делать большие шаги, даже если рассматриваемая точка близка к границе допустимой области. ^[5]^{: 337}

Формально итерационный метод, лежащий в основе аффинного масштабирования, принимает в качестве входных данных $A$ , $b$ , $c$ , строго выполнимое начальное предположение $x 0 > 0$ (то есть $Ax 0 = b$ ), допуск $ε$ и размер шага $β$ . Затем выполняется итерация ^[1]^{: 111}

Пусть $D k$ - диагональная матрица с $x k$ на ее диагонали.
Вычислите вектор двойных переменных:
${\ displaystyle w ^ {k} = (AD_ {k} ^ {2} A ^ {\ operatorname {T}}) ^ {- 1} AD_ {k} ^ {2} c.}$
Вычислите вектор приведенных затрат , который измеряет слабость ограничений неравенства в двойном:
$r^{k}=c-A^{\operatorname {T} }w^{k}.$
Если и , текущее решение $x$ $k$ является $ε$ -оптимальным. $r^{k}>0$ $\mathbf {1} ^{\operatorname {T} }D_{k}r^{k}<\varepsilon$
Если , проблема безгранична. $-D_{k}r^{k}\geq 0$
Обновлять $x^{k+1}=x^{k}-\beta {\frac {D_{k}^{2}r^{k}}{\|D_{k}r^{k}\|}}$

Инициализация [ править ]

Фаза I, инициализация, решает вспомогательную задачу с дополнительной переменной $u$ и использует результат для определения начальной точки исходной задачи. Пусть $x 0$ - произвольная строго положительная точка; это не обязательно должно быть выполнимым для исходной проблемы. Невыполнимость $x 0$ измеряется вектором

v=b-Ax^{0}

.

Если $v = 0$ , возможно $x 0$ . В противном случае этап I решает вспомогательную задачу.

свернуть

тебя

при условии

Ax + uv = b

,

x \geq 0

,

u \geq 0

.

Эта проблема имеет правильную форму для решения с помощью описанного выше итерационного алгоритма ^[a] и

{\begin{pmatrix}x^{0}\\1\end{pmatrix}}

это возможная начальная точка. Решение вспомогательной задачи дает

{\begin{pmatrix}x^{*}\\u^{*}\end{pmatrix}}

.

Если $u * = 0$ , то $x * = 0$ выполнимо в исходной задаче (хотя и не обязательно строго внутренней), а если $u * > 0$ , исходная проблема недопустима. ^[5]^{: 343}

Анализ [ править ]

Хотя аффинное масштабирование легко сформулировать, было трудно проанализировать. Его сходимость зависит от размера шага $β$ . Для размеров шага $β \leq 2 / 3$ , Вариант аффинного масштабирования Вандербея сходится, в то время как для $β > 0,995$ известен пример проблемы, которая сходится к субоптимальному значению. ^[5]^{: 342} Было показано, что другие варианты алгоритма демонстрируют хаотическое поведение даже на небольших задачах, когда $β > 2 / 3$ . ^[6]^[7]

Примечания [ править ]

^ Структура вспомогательной задачи позволяет упростить формулы. ^[5]^{: 344}

Ссылки [ править ]

^ a b c Vanderbei, RJ; Лагариас, JC (1990). «Результат сходимости И. И. Дикина для алгоритма аффинного масштабирования». Математические разработки, вытекающие из линейного программирования (Brunswick, ME, 1988) . Современная математика. 114 . Провиденс, Род-Айленд: Американское математическое общество. С. 109–119. DOI : 10.1090 / conm / 114/1097868 . Руководство по ремонту 1097868 .
^ Барнс, Эрл Р. (1986). «Вариант алгоритма Кармаркара для решения задач линейного программирования». Математическое программирование . 36 (2): 174–182. DOI : 10.1007 / BF02592024 .
^ Вандербей, Роберт Дж .; Meketon, Marc S .; Фридман, Барри А. (1986). «Модификация алгоритма линейного программирования Кармаркара» (PDF) . Алгоритмика . 1 (1–4): 395–407. DOI : 10.1007 / BF01840454 .
^ Байер, DA; Лагариас, JC (1989). «Нелинейная геометрия линейного программирования I: аффинные и проективные масштабные траектории» (PDF) . Труды Американского математического общества . 314 (2): 499. DOI : 10.1090 / S0002-9947-1989-1005525-6 .
^ а б в г е Вандербей, Роберт Дж. (2001). Линейное программирование: основы и расширения . Springer Verlag. С. 333–347.
^ Bruin, H .; Фоккинк, Р.Дж.; Gu, G .; Роос, К. (2014). «О хаотическом поведении алгоритма прямого двойственного аффинного масштабирования для линейной оптимизации» (PDF) . Хаос . 24 (4): 043132. arXiv : 1409.6108 . Bibcode : 2014Chaos..24d3132B . DOI : 10.1063 / 1.4902900 . PMID 25554052 .
^ Кастильо, Илеана; Барнс, Эрл Р. (2006). «Хаотическое поведение алгоритма аффинного масштабирования для линейного программирования». SIAM J. Optim . 11 (3): 781–795. DOI : 10.1137 / S1052623496314070 .

Дальнейшее чтение [ править ]

Адлер, Илан; Монтейро, Ренато, округ Колумбия (1991). «Предельное поведение аффинных масштабируемых непрерывных траекторий для задач линейного программирования» (PDF) . Математическое программирование . 50 (1–3): 29–51. DOI : 10.1007 / bf01594923 .
Сайгал, Ромеш (1996). «Простое доказательство первичного метода аффинного масштабирования» (PDF) . Анналы исследований операций . 62 : 303–324. DOI : 10.1007 / bf02206821 .
Ценг, Пол; Ло, Чжи-Цюань (1992). «О сходимости алгоритма аффинного масштабирования» (PDF) . Математическое программирование . 56 (1–3): 301–319. CiteSeerX 10.1.1.94.7852 . DOI : 10.1007 / bf01580904 . ЛВП : 1721,1 / 3161 .

Внешние ссылки [ править ]

«15.093 Методы оптимизации, Лекция 21: Алгоритм аффинного масштабирования» (PDF) . MIT OpenCourseWare . 2009 г.
Митчелл, Джон (ноябрь 2010 г.). «Методы внутренней точки» . Политехнический институт Ренсселера .
«Лекция 6: Метод внутренней точки» (PDF) . NCTU OpenCourseWare . Архивировано из оригинального (PDF) 11 октября 2016 года . Проверено 6 февраля 2016 .

[6] Структура вспомогательной задачи позволяет упростить формулы. ^[5]^{: 344}

[vanderbei90-1] Vanderbei, RJ; Лагариас, JC (1990). «Результат сходимости И. И. Дикина для алгоритма аффинного масштабирования». Математические разработки, вытекающие из линейного программирования (Brunswick, ME, 1988) . Современная математика. 114 . Провиденс, Род-Айленд: Американское математическое общество. С. 109–119. DOI : 10.1090 / conm / 114/1097868 . Руководство по ремонту 1097868 .

[2] Барнс, Эрл Р. (1986). «Вариант алгоритма Кармаркара для решения задач линейного программирования». Математическое программирование . 36 (2): 174–182. DOI : 10.1007 / BF02592024 .

[3] Вандербей, Роберт Дж .; Meketon, Marc S .; Фридман, Барри А. (1986). «Модификация алгоритма линейного программирования Кармаркара» (PDF) . Алгоритмика . 1 (1–4): 395–407. DOI : 10.1007 / BF01840454 .

[4] Байер, DA; Лагариас, JC (1989). «Нелинейная геометрия линейного программирования I: аффинные и проективные масштабные траектории» (PDF) . Труды Американского математического общества . 314 (2): 499. DOI : 10.1090 / S0002-9947-1989-1005525-6 .

[lpfe-5] а б в г е Вандербей, Роберт Дж. (2001). Линейное программирование: основы и расширения . Springer Verlag. С. 333–347.

[7] Bruin, H .; Фоккинк, Р.Дж.; Gu, G .; Роос, К. (2014). «О хаотическом поведении алгоритма прямого двойственного аффинного масштабирования для линейной оптимизации» (PDF) . Хаос . 24 (4): 043132. arXiv : 1409.6108 . Bibcode : 2014Chaos..24d3132B . DOI : 10.1063 / 1.4902900 . PMID 25554052 .

[8] Кастильо, Илеана; Барнс, Эрл Р. (2006). «Хаотическое поведение алгоритма аффинного масштабирования для линейного программирования». SIAM J. Optim . 11 (3): 781–795. DOI : 10.1137 / S1052623496314070 .

[1]. ]