Метод внутренней точки

Методы внутренней точки (также называемые барьерными методами или IPM ) представляют собой определенный класс алгоритмов , решающих линейные и нелинейные задачи выпуклой оптимизации .

Пример поиска решения. Фиолетовые линии показывают ограничения, красные точки показывают повторяющиеся решения.

Джон фон Нейман ^[1] предложил метод линейного программирования внутренней точки, который не был ни методом полиномиального времени, ни эффективным методом на практике. На самом деле он оказался медленнее, чем обычно используемый симплексный метод .

Метод внутренней точки был открыт советским математиком И.И. Дикиным в 1967 году и заново изобретен в США в середине 1980-х годов. В 1984 году Нарендра Кармаркар разработал метод линейного программирования, названный алгоритмом Кармаркара , который работает за доказуемо полиномиальное время и также очень эффективен на практике. Это позволило решить задачи линейного программирования, которые выходили за рамки возможностей симплекс-метода. В отличие от симплексного метода, наилучшее решение достигается путем обхода внутренней части допустимой области . Метод может быть обобщен на выпуклое программирование на основе самосогласованной барьерной функции, используемой для кодирования выпуклого множества .

Любая задача выпуклой оптимизации может быть преобразована в минимизацию (или максимизацию) линейной функции над выпуклым множеством путем преобразования в форму надграфика . ^[2] Идея кодирования допустимого множества с помощью барьера и разработки барьерных методов была изучена Энтони В. Юрий Нестеров и Аркадий Немировский разработали специальный класс таких барьеров, которые можно использовать для кодирования любого выпуклого множества. Они гарантируют, что количество итераций алгоритма ограничено полиномом по размерности и точности решения. ^[3]

Прорыв Кармаркара возродил изучение методов внутренней точки и проблем с барьерами, показав, что можно создать алгоритм для линейного программирования, характеризующийся полиномиальной сложностью и, более того, который конкурирует с симплекс-методом. Уже Хачиян «S эллипсоид метод был полиномиальный алгоритм времени; однако это было слишком медленно, чтобы представлять практический интерес.

Класс методов прямого двойственного следования по внутренним точкам считается наиболее успешным.Алгоритм предиктора-корректора Mehrotra обеспечивает основу для большинства реализаций этого класса методов. ^[4]

Первично-дуальный метод внутренней точки для нелинейной оптимизации [ править ]

Идею первично-двойственного метода легко продемонстрировать для нелинейной оптимизации с ограничениями . Для простоты рассмотрим вариант задачи нелинейной оптимизации с полным неравенством:

минимизировать в зависимости от того, где

{\ displaystyle f (x)}

{\ displaystyle c_ {i} (x) \ geq 0 ~ {\ text {for}} ~ i = 1, \ ldots, m, ~ x \ in \ mathbb {R} ^ {n},}

{\ displaystyle f: \ mathbb {R} ^ {n} \ to \ mathbb {R}, c_ {i}: \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} \ quad (1).}

Логарифмическая барьерная функция, связанная с (1), равна

{\ Displaystyle В (х, \ му) = е (х) - \ му \ сумма _ {я = 1} ^ {м} \ журнал (c_ {я} (х)). \ quad (2)}

Вот небольшой положительный скаляр, иногда называемый «параметром барьера». При сходе к нулю минимум должен сходиться к решению (1). ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$ ${\ Displaystyle В (х, \ му)}$

Градиент барьерной функции равен

{\ displaystyle g_ {b} = g- \ mu \ sum _ {i = 1} ^ {m} {\ frac {1} {c_ {i} (x)}} \ nabla c_ {i} (x), \ quad (3)}

где - градиент исходной функции , а - градиент . ${\ displaystyle g}$ ${\ displaystyle f (x)}$ ${\ displaystyle \ nabla c_ {i}}$ ${\ displaystyle c_ {i}}$

В дополнение к исходной («первичной») переменной мы вводим двойную переменную, вдохновленную множителем Лагранжа. ${\ displaystyle x}$ ${\ displaystyle \ lambda \ in \ mathbb {R} ^ {m}}$

{\ displaystyle c_ {i} (x) \ lambda _ {i} = \ mu, \ forall i = 1, \ ldots, m. \ quad (4)}

(4) иногда называют условием «возмущенной дополнительности» из-за его сходства с «дополнительным провисанием» в условиях KKT .

Мы пытаемся найти те, для которых градиент барьерной функции равен нулю. $(x_{\mu },\lambda _{\mu })$

Применяя (4) к (3), получаем уравнение для градиента:

g-A^{T}\lambda =0,\quad (5)

где матрица - якобиан ограничений . $A$ $c(x)$

Интуиция, стоящая за (5), заключается в том, что градиент должен лежать в подпространстве, охватываемом градиентами ограничений. «Возмущенная дополнительность» с малым (4) может пониматься как условие, при котором решение либо должно находиться вблизи границы , либо проекция градиента на нормаль компонента ограничения должна быть почти нулевой. $f(x)$ $\mu$ $c_{i}(x)=0$ $g$ $c_{i}(x)$

Применяя метод Ньютона к (4) и (5), мы получаем уравнение для обновления : $(x,\lambda )$ $(p_{x},p_{\lambda })$

{\begin{pmatrix}W&-A^{T}\\\Lambda A&C\end{pmatrix}}{\begin{pmatrix}p_{x}\\p_{\lambda }\end{pmatrix}}={\begin{pmatrix}-g+A^{T}\lambda \\\mu 1-C\lambda \end{pmatrix}},

где есть матрица Гесса из , является диагональной матрицей из , и является диагональной матрицей с . $W$ $B(x,\mu )$ $\Lambda$ $\lambda$ $C$ $C_{ii}=c_{i}(x)$

В силу (1), (4) условие

\lambda \geq 0

должны соблюдаться на каждом этапе. Это можно сделать, выбрав подходящие : $\alpha$

(x,\lambda )\to (x+\alpha p_{x},\lambda +\alpha p_{\lambda }).

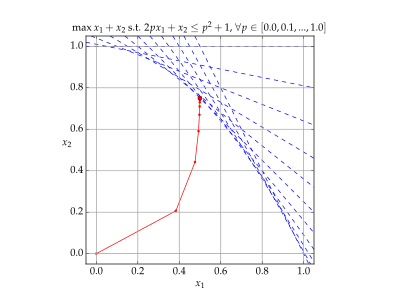
Воспроизвести медиа

Траектория итераций x с использованием метода внутренней точки.

См. Также [ править ]

Аффинное масштабирование
Дополненный лагранжев метод
Штрафной метод
Условия Каруша – Куна – Таккера.

Ссылки [ править ]

^ Данциг, Джордж Б .; Тапа, Мукунд Н. (2003). Линейное программирование 2: теория и расширения . Springer-Verlag.
^ Бойд, Стивен; Ванденберге, Ливен (2004). Выпуклая оптимизация . Кембридж: Издательство Кембриджского университета . п. 143. ISBN. 978-0-521-83378-3. Руководство по ремонту 2061575 .
^ Райт, Маргарет Х. (2004). «Революция внутренней точки в оптимизации: история, недавние события и долгосрочные последствия» . Бюллетень Американского математического общества . 42 : 39–57. DOI : 10.1090 / S0273-0979-04-01040-7 . Руководство по ремонту 2115066 .
^ Потра, Флориан А .; Стивен Дж. Райт (2000). «Внутренние точечные методы» . Журнал вычислительной и прикладной математики . 124 (1–2): 281–302. DOI : 10.1016 / S0377-0427 (00) 00433-7 .

Библиография [ править ]

Дикин, II (1967). «Итерационное решение задач линейного и квадратичного программирования» . Докл. Акад. АН СССР . 174 (1): 747–748.
Боннанс, Ж. Фредерик; Гилберт, Дж. Чарльз; Лемарешаль, Клод ; Сагастизабал, Клаудиа А. (2006). Численная оптимизация: теоретические и практические аспекты . Universitext (Второе исправленное издание перевода французского издания 1997 г.). Берлин: Springer-Verlag. С. xiv + 490. DOI : 10.1007 / 978-3-540-35447-5 . ISBN 978-3-540-35445-1. Руководство по ремонту 2265882 . CS1 maint: discouraged parameter (link)
Кармаркар, Н. (1984). «Новый алгоритм полиномиального времени для линейного программирования» (PDF) . Материалы шестнадцатого ежегодного симпозиума ACM по теории вычислений - STOC '84 . п. 302. DOI : 10,1145 / 800057,808695 . ISBN 0-89791-133-4. Архивировано из оригинального (PDF) 28 декабря 2013 года.
Мехротра, Санджай (1992). «О реализации метода первично-дуальной внутренней точки». SIAM Journal по оптимизации . 2 (4): 575–601. DOI : 10.1137 / 0802028 .
Нокедаль, Хорхе; Стивен Райт (1999). Численная оптимизация . Нью-Йорк, штат Нью-Йорк: Спрингер. ISBN 978-0-387-98793-4.
Нажмите, WH; Теукольский, С.А. Феттерлинг, Вашингтон; Фланнери, ВР (2007). «Раздел 10.11. Линейное программирование: методы внутренней точки» . Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-88068-8.
Райт, Стивен (1997). Первоначально-двойственные методы внутренней точки . Филадельфия, Пенсильвания: SIAM. ISBN 978-0-89871-382-4.
Бойд, Стивен; Ванденберге, Ливен (2004). Выпуклая оптимизация (PDF) . Издательство Кембриджского университета.

[1] Данциг, Джордж Б .; Тапа, Мукунд Н. (2003). Линейное программирование 2: теория и расширения . Springer-Verlag.

[2] Бойд, Стивен; Ванденберге, Ливен (2004). Выпуклая оптимизация . Кембридж: Издательство Кембриджского университета . п. 143. ISBN. 978-0-521-83378-3. Руководство по ремонту 2061575 .

[3] Райт, Маргарет Х. (2004). «Революция внутренней точки в оптимизации: история, недавние события и долгосрочные последствия» . Бюллетень Американского математического общества . 42 : 39–57. DOI : 10.1090 / S0273-0979-04-01040-7 . Руководство по ремонту 2115066 .

[4] Потра, Флориан А .; Стивен Дж. Райт (2000). «Внутренние точечные методы» . Журнал вычислительной и прикладной математики . 124 (1–2): 281–302. DOI : 10.1016 / S0377-0427 (00) 00433-7 .

[1]