Координатный спуск

Координатный спуск - это алгоритм оптимизации, который последовательно минимизирует вдоль координатных направлений, чтобы найти минимум функции. На каждой итерации алгоритм определяет координату или блок координат с помощью правила выбора координат, затем точно или неточно минимизирует по соответствующей гиперплоскости координат, фиксируя все другие координаты или блоки координат. Поиск линии вдоль координат направления может быть выполнен в текущей итерации для определения соответствующего размера шага. Координатный спуск применим как в дифференцируемом, так и в свободном от производных контекстах.

Описание [ править ]

Координатный спуск основан на идее, что минимизация функции многих переменных может быть достигнута путем минимизации ее в одном направлении за раз, то есть путем решения одномерных (или, по крайней мере, более простых) задач оптимизации в цикле. ^[1] В простейшем случае циклического спуска координат выполняется циклическая итерация по направлениям по одному, минимизируя целевую функцию по каждому направлению координат за раз. То есть начиная с начальных значений переменных ${\ Displaystyle F (\ mathbf {x})}$

{\ displaystyle \ mathbf {x} ^ {0} = (x_ {1} ^ {0}, \ ldots, x_ {n} ^ {0})}

,

round определяет от путем итеративного решения задач оптимизации с одной переменной ${\ displaystyle k + 1}$ ${\ Displaystyle \ mathbf {х} ^ {к + 1}}$ ${\ displaystyle \ mathbf {x} ^ {k}}$

{\ displaystyle x_ {i} ^ {k + 1} = {\ underset {y \ in \ mathbb {R}} {\ operatorname {arg \, min}}} \; f (x_ {1} ^ {k + 1}, \ dots, x_ {i-1} ^ {k + 1}, y, x_ {i + 1} ^ {k}, \ dots, x_ {n} ^ {k})}

^[2]

для каждой переменной из , за от 1 до . ${\ displaystyle x_ {i}}$ $\mathbf {x}$ $i$ $n$

Таким образом, каждый начинает с первоначального предположения для локального минимума и итеративно получает последовательность . $\mathbf {x} ^{0}$ $F$ $\mathbf {x} ^{0},\mathbf {x} ^{1},\mathbf {x} ^{2},\dots$

Выполняя линейный поиск на каждой итерации, автоматически получается

F(\mathbf {x} ^{0})\geq F(\mathbf {x} ^{1})\geq F(\mathbf {x} ^{2})\geq \dots .

Можно показать, что эта последовательность имеет свойства сходимости, аналогичные свойствам наискорейшего спуска. Отсутствие улучшения после одного цикла поиска линии вдоль координатных направлений означает достижение стационарной точки.

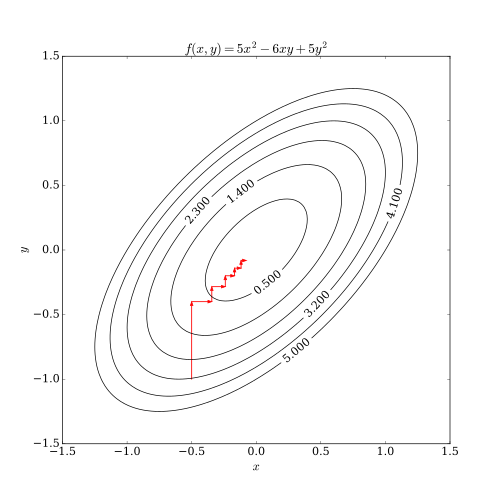
Этот процесс проиллюстрирован ниже.

Дифференцируемый случай [ править ]

В случае непрерывно дифференцируемой функции $F$ алгоритм покоординатного спуска можно набросать следующим образом: ^[1]

Выберите начальный вектор параметров $x$ .
Пока не будет достигнута сходимость, или для некоторого фиксированного количества итераций:
- Выберите индекс $i$ от $1$ до $n$ .
- Выберите размер шага $α$ .
- Обновить $x i$ до $x i - α \partial F / \partial х я (х)$ .

Размер шага может быть выбран различными способами, например, путем решения точного минимизатора $f (x i) = F (x)$ (т. Е. $F$ со всеми переменными, кроме фиксированного $x i$ ), или с помощью традиционных критериев поиска строки. ^[1]

Ограничения [ править ]

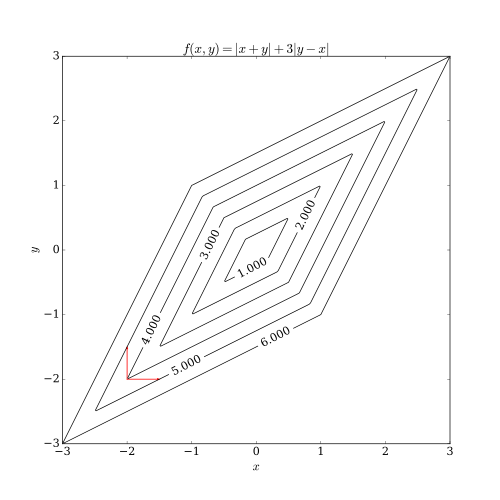
Координатный спуск имеет две проблемы. Один из них , имеющий не- гладких многомерных функций. На следующем рисунке показано, что итерация спуска координат может застрять в нестационарной точке, если кривые уровня функции не являются гладкими. Предположим, что алгоритм находится в точке $(-2, -2)$ ; тогда есть два выровненных по оси направления, которые он может рассмотреть для шага, обозначенных красными стрелками. Однако каждый шаг в этих двух направлениях будет увеличивать значение целевой функции (предполагая задачу минимизации), поэтому алгоритм не будет предпринимать никаких шагов, даже если оба шага вместе приблизят алгоритм к оптимальному. Хотя этот пример показывает, что спуск координат не обязательно сходится к оптимуму, можно показать формальную сходимость при разумных условиях. ^[3]

Другая проблема - сложность параллелизма. Поскольку природа спуска координат заключается в циклическом перемещении по направлениям и минимизации целевой функции по каждому направлению координат, спуск координат не является очевидным кандидатом на массовый параллелизм. Недавние исследования показали, что массовый параллелизм применим к координатному спуску, ослабляя изменение целевой функции по каждому координатному направлению. ^[4]^[5]^[6]

Приложения [ править ]

Алгоритмы координатного спуска популярны среди практиков благодаря своей простоте, но это же свойство привело к тому, что исследователи оптимизации в значительной степени игнорировали их в пользу более интересных (сложных) методов. ^[1] Раннее применение оптимизации спуска координат было в области компьютерной томографии ^[7], где было обнаружено, что она имеет быструю сходимость ^[8] и впоследствии использовалась для клинической реконструкции многосрезового спирального сканирования CT. ^[9] Алгоритм циклического координатного спуска (CCD) был применен в предсказании структуры белка. ^[10] Более того, интерес к использованию координатного спуска возрос с появлением крупномасштабных задач в машинном обучении., где координатный спуск оказался конкурентоспособным по сравнению с другими методами при применении к таким задачам, как обучение линейных опорных векторных машин ^[11] (см. LIBLINEAR ) и факторизацию неотрицательной матрицы . ^[12] Они привлекательны для задач, в которых вычисление градиентов невозможно, возможно, потому, что данные, необходимые для этого, распределяются по компьютерным сетям. ^[13]

См. Также [ править ]

Адаптивный координатный спуск
Сопряженный градиент
Градиентный спуск
Линейный поиск
Математическая оптимизация
Метод Ньютона
Стохастический градиентный спуск - использует один пример за раз, а не одну координату

Ссылки [ править ]

^ а б в г Райт, Стивен Дж. (2015). «Алгоритмы координатного спуска». Математическое программирование . 151 (1): 3–34. arXiv : 1502.04759 . DOI : 10.1007 / s10107-015-0892-3 .
^ https://www.cs.cmu.edu/~ggordon/10725-F12/slides/25-coord-desc.pdf
Перейти ↑ Spall, JC (2012). «Циклический процесс качелей для оптимизации и идентификации». Журнал теории оптимизации и приложений . 154 (1): 187–208. DOI : 10.1007 / s10957-012-0001-1 .
^ Zheng, J .; Сакиб, СС; Sauer, K .; Боуман, Калифорния (2000-10-01). «Параллелизуемые байесовские алгоритмы томографии с быстрой гарантированной сходимостью». IEEE Transactions по обработке изображений . 9 (10): 1745–1759. Bibcode : 2000ITIP .... 9.1745Z . CiteSeerX 10.1.1.34.4282 . DOI : 10.1109 / 83.869186 . ISSN 1057-7149 . PMID 18262913 .
^ Fessler, JA; Ficaro, EP; Клинторн, штат Нью-Хэмпшир; Ланге, К. (1997-04-01). "Алгоритмы восхождения сгруппированных координат для восстановления изображения передачи с штрафным правдоподобием". IEEE Transactions по медицинской визуализации . 16 (2): 166–175. DOI : 10.1109 / 42.563662 . ЛВП : 2027,42 / 86021 . ISSN 0278-0062 . PMID 9101326 .
^ Ван, Сяо; Сабне, Амит; Киснер, Шерман; Рагхунатан, Ананд; Боуман, Шарль; Мидкифф, Сэмюэл (01.01.2016). Высокопроизводительная реконструкция изображения на основе модели . Материалы 21-го симпозиума ACM SIGPLAN по принципам и практике параллельного программирования . ППоПП '16. Нью-Йорк, Нью-Йорк, США: ACM. С. 2: 1–2: 12. DOI : 10.1145 / 2851141.2851163 . ISBN 9781450340922.
^ Зауэр, Кен; Боуман, Чарльз (февраль 1993 г.). «Стратегия локального обновления для итеративной реконструкции из прогнозов» (PDF) . Транзакции IEEE по обработке сигналов . 41 (2): 534–548. Bibcode : 1993ITSP ... 41..534S . CiteSeerX 10.1.1.135.6045 . DOI : 10.1109 / 78.193196 .
^ Ю, Чжоу; Тибо, Жан-Батист; Боуман, Шарль; Зауэр, Кен; Се, Цзян (январь 2011 г.). «Быстрая модельная реконструкция рентгеновской компьютерной томографии с использованием пространственно неоднородной оптимизации ИКД» (PDF) . IEEE Transactions по обработке изображений . 20 (1): 161–175. Bibcode : 2011ITIP ... 20..161Y . DOI : 10.1109 / TIP.2010.2058811 . PMID 20643609 .
^ Тибо, Жан-Батист; Зауэр, Кен; Боуман, Шарль; Се, Цзян (ноябрь 2007 г.). «Трехмерный статистический подход к улучшению качества изображения для многосрезовой спиральной компьютерной томографии» (PDF) . Медицинская физика . 34 (11): 4526–4544. Bibcode : 2007MedPh..34.4526T . DOI : 10.1118 / 1.2789499 . PMID 18072519 .
^ Канутеску, AA; Данбрак, Р.Л. (2003). «Циклический координатный спуск: алгоритм робототехники для замыкания белковой петли» . Белковая наука . 12 (5): 963–72. DOI : 10.1110 / ps.0242703 . PMC 2323867 . PMID 12717019 .
^ Hsieh, CJ; Чанг, кВт; Lin, CJ; Кирти, СС; Сундарараджан, С. (2008). «Метод двойного координатного спуска для крупномасштабной линейной SVM» (PDF) . Материалы 25-й международной конференции по машинному обучению - ICML '08 . п. 408. DOI : 10,1145 / 1390156,1390208 . ISBN 9781605582054.
^ Hsieh, CJ; Диллон, IS (2011). Методы быстрого координатного спуска с выбором переменных для неотрицательной матричной факторизации (PDF) . Материалы 17-й международной конференции ACM SIGKDD по открытию знаний и интеллектуальному анализу данных - KDD '11. п. 1064. DOI : 10,1145 / 2020408,2020577 . ISBN 9781450308137.
↑ Нестеров, Юрий (2012). «Эффективность методов координатного спуска в задачах оптимизации большого масштаба» (PDF) . SIAM J. Optim . 22 (2): 341–362. CiteSeerX 10.1.1.332.3336 . DOI : 10.1137 / 100802001 .

Бездек, JC; Hathaway, RJ; Ховард, RE; Уилсон, Калифорния; Виндхэм, член парламента (1987), "Анализ локальной сходимости версии сгруппированных переменных координатного спуска", Журнал теории оптимизации и приложений , Kluwer Academic / Plenum Publishers, 54 (3), стр. 471–477, doi : 10.1007 / BF00940196
Бертсекас, Дмитрий П. (1999). Нелинейное программирование, второе издание Athena Scientific, Белмонт, Массачусетс. ISBN 1-886529-00-0 .
Ло, Чжицюань; Ценг, П. (1992), "О сходимости метода координатного спуска для выпуклой дифференцируемой минимизации", Журнал теории оптимизации и приложений , Kluwer Academic / Plenum Publishers, 72 (1), стр. 7–35, doi : 10.1007 / BF00939948 , ЛВП : 1721,1 / 3164.
Ву, Тонгтонг; Ланге, Кеннет (2008), «Алгоритмы координатного спуска для регрессии со штрафом Лассо», Анналы прикладной статистики , Институт математической статистики, 2 (1), стр. 224–244, arXiv : 0803.3876 , doi : 10.1214 / 07-AOAS147.
Ричтарик, Питер; Такач, Мартин (апрель 2011 г.), «Итерационная сложность рандомизированных методов блочно-координатного спуска для минимизации составной функции», Математическое программирование , Springer, 144 (1–2), стр. 1–38, arXiv : 1107.2848 , doi : 10.1007 / s10107-012-0614-z.
Ричтарик, Питер; Такач, Мартин (декабрь 2012 г.), «Методы параллельного спуска координат для оптимизации больших данных», ArXiv: 1212.0873 , arXiv : 1212.0873.

[wright-1] а б в г Райт, Стивен Дж. (2015). «Алгоритмы координатного спуска». Математическое программирование . 151 (1): 3–34. arXiv : 1502.04759 . DOI : 10.1007 / s10107-015-0892-3 .

[2] ttps://www.cs.cmu.edu/~ggordon/10725-F12/slides/25-coord-desc.pdf

[3] Перейти ↑ Spall, JC (2012). «Циклический процесс качелей для оптимизации и идентификации». Журнал теории оптимизации и приложений . 154 (1): 187–208. DOI : 10.1007 / s10957-012-0001-1 .

[4] Zheng, J .; Сакиб, СС; Sauer, K .; Боуман, Калифорния (2000-10-01). «Параллелизуемые байесовские алгоритмы томографии с быстрой гарантированной сходимостью». IEEE Transactions по обработке изображений . 9 (10): 1745–1759. Bibcode : 2000ITIP .... 9.1745Z . CiteSeerX 10.1.1.34.4282 . DOI : 10.1109 / 83.869186 . ISSN 1057-7149 . PMID 18262913 .

[5] Fessler, JA; Ficaro, EP; Клинторн, штат Нью-Хэмпшир; Ланге, К. (1997-04-01). "Алгоритмы восхождения сгруппированных координат для восстановления изображения передачи с штрафным правдоподобием". IEEE Transactions по медицинской визуализации . 16 (2): 166–175. DOI : 10.1109 / 42.563662 . ЛВП : 2027,42 / 86021 . ISSN 0278-0062 . PMID 9101326 .

[6] Ван, Сяо; Сабне, Амит; Киснер, Шерман; Рагхунатан, Ананд; Боуман, Шарль; Мидкифф, Сэмюэл (01.01.2016). Высокопроизводительная реконструкция изображения на основе модели . Материалы 21-го симпозиума ACM SIGPLAN по принципам и практике параллельного программирования . ППоПП '16. Нью-Йорк, Нью-Йорк, США: ACM. С. 2: 1–2: 12. DOI : 10.1145 / 2851141.2851163 . ISBN 9781450340922.

[7] Зауэр, Кен; Боуман, Чарльз (февраль 1993 г.). «Стратегия локального обновления для итеративной реконструкции из прогнозов» (PDF) . Транзакции IEEE по обработке сигналов . 41 (2): 534–548. Bibcode : 1993ITSP ... 41..534S . CiteSeerX 10.1.1.135.6045 . DOI : 10.1109 / 78.193196 .

[8] Ю, Чжоу; Тибо, Жан-Батист; Боуман, Шарль; Зауэр, Кен; Се, Цзян (январь 2011 г.). «Быстрая модельная реконструкция рентгеновской компьютерной томографии с использованием пространственно неоднородной оптимизации ИКД» (PDF) . IEEE Transactions по обработке изображений . 20 (1): 161–175. Bibcode : 2011ITIP ... 20..161Y . DOI : 10.1109 / TIP.2010.2058811 . PMID 20643609 .

[9] Тибо, Жан-Батист; Зауэр, Кен; Боуман, Шарль; Се, Цзян (ноябрь 2007 г.). «Трехмерный статистический подход к улучшению качества изображения для многосрезовой спиральной компьютерной томографии» (PDF) . Медицинская физика . 34 (11): 4526–4544. Bibcode : 2007MedPh..34.4526T . DOI : 10.1118 / 1.2789499 . PMID 18072519 .

[10] Канутеску, AA; Данбрак, Р.Л. (2003). «Циклический координатный спуск: алгоритм робототехники для замыкания белковой петли» . Белковая наука . 12 (5): 963–72. DOI : 10.1110 / ps.0242703 . PMC 2323867 . PMID 12717019 .

[11] Hsieh, CJ; Чанг, кВт; Lin, CJ; Кирти, СС; Сундарараджан, С. (2008). «Метод двойного координатного спуска для крупномасштабной линейной SVM» (PDF) . Материалы 25-й международной конференции по машинному обучению - ICML '08 . п. 408. DOI : 10,1145 / 1390156,1390208 . ISBN 9781605582054.

[12] Hsieh, CJ; Диллон, IS (2011). Методы быстрого координатного спуска с выбором переменных для неотрицательной матричной факторизации (PDF) . Материалы 17-й международной конференции ACM SIGKDD по открытию знаний и интеллектуальному анализу данных - KDD '11. п. 1064. DOI : 10,1145 / 2020408,2020577 . ISBN 9781450308137.

[13] Нестеров, Юрий (2012). «Эффективность методов координатного спуска в задачах оптимизации большого масштаба» (PDF) . SIAM J. Optim . 22 (2): 341–362. CiteSeerX 10.1.1.332.3336 . DOI : 10.1137 / 100802001 .

[1]