Корона граф

Корона граф
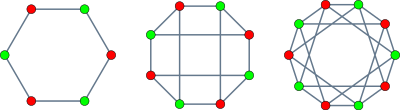Графы короны с шестью, восемью и десятью вершинами
Вершины	2 п
Края	п ( п - 1)
Радиус	${\ displaystyle \ left \ {{\ begin {array} {ll} \ infty & n \ leq 2 \\ 3 & {\ text {else}} \ end {array}} \ right.}$
Диаметр	${\ displaystyle \ left \ {{\ begin {array} {ll} \ infty & n \ leq 2 \\ 3 & {\ text {else}} \ end {array}} \ right.}$
Обхват	${\ displaystyle \ left \ {{\ begin {array} {ll} \ infty & n \ leq 2 \\ 6 & n = 3 \\ 4 & {\ text {else}} \ end {array}} \ right.}$
Хроматическое число	${\ displaystyle \ left \ {{\ begin {array} {ll} 1 & n = 1 \\ 2 & {\ text {else}} \ end {array}} \ right.}$
Характеристики	Дистанционно-транзитивный
Обозначение	${\ Displaystyle S_ {п} ^ {0}}$
Таблица графиков и параметров

В теории графов , разделе математики, граф короны на 2 n вершинах - это неориентированный граф с двумя наборами вершин { u ₁ , u ₂ , ..., u _n } и { v ₁ , v ₂ , ... , v _n } и ребром от u _i до v _j, если i  ≠  j .

Краун график можно рассматривать как полный двудольный граф , из которого ребра паросочетания были удалены, как двудольный двойной крышкой из более полного графа , как тензорное произведение К _п × K ₂ , в качестве дополнения к декартово прямой произведение K _n и K ₂ , или как двудольный граф Кнезера H _{n , 1,} представляющий  подмножества из 1 и ( n - 1) -элементов набора из n элементов, с ребром между двумя подмножествами, если один из другой.

Примеры [ править ]

Граф короны с 6 вершинами образует цикл , а граф с 8 вершинами изоморфен графу куба . В двойной шестерке Шлефли , конфигурации из 12 линий и 30 точек в трехмерном пространстве, двенадцать линий пересекаются друг с другом по образцу графа короны с 12 вершинами.

Свойства [ править ]

Бикликовое покрытие десятивершинного графа короны

Количество ребер в графе короны - это проническое число n ( n  - 1). Его ахроматическое число является п : можно найти полную окраску , выбирая каждую пару { U _я , v _я } в качестве одного из цветовых классов. ^[1] Коронные графы симметричны и дистанционно транзитивны . Архидиакон и др. (2004) описывают разбиение ребер графа короны на циклы равной длины.

Граф короны с 2 n вершинами может быть вложен в четырехмерное евклидово пространство таким образом, что все его ребра имеют единичную длину. Однако это вложение может также разместить некоторые несмежные вершины на единичном расстоянии друг от друга. Вложение, в котором края находятся на единичном расстоянии, а не ребра не на единичном расстоянии, требует как минимум n  - 2 измерений. Этот пример показывает, что для графа могут потребоваться очень разные измерения, которые будут представлены как графы единичных расстояний и как строгие графы единичных расстояний. ^[2]

Минимальное количество полных двудольных подграфов, необходимых для покрытия ребер коронного графа (его двудольный размер или размер минимального бикликового покрытия), равно

${\ Displaystyle \ sigma (п) = \ мин \ влево \ {\, к \ середина п \ leq {\ binom {k} {\ lfloor k / 2 \ rfloor}} \, \ right \},}$

функция, обратная центральному биномиальному коэффициенту . ^[3]

Дополнение граф из 2 п графа -vertex короны является декартово произведением из полных графов K ₂ K _п , или , что эквивалентно 2 ×  н Ладейного графа .${\ Displaystyle \ квадрат}$

Приложения [ править ]

В этикете традиционным правилом размещения гостей за обеденным столом является то, что мужчины и женщины должны чередоваться позы и ни одна супружеская пара не должна сидеть рядом друг с другом. ^[4] Расстановки, удовлетворяющие этому правилу, для группы, состоящей из n супружеских пар, могут быть описаны как гамильтоновы циклы графа короны. Например, расположение вершин, показанное на рисунке, можно интерпретировать как схемы рассадки этого типа, в которых каждый муж и жена сидят как можно дальше друг от друга. Проблема подсчета количества возможных расстановок мест, или почти эквивалентно ^[5] количества гамильтоновых циклов в графе короны, известна в комбинаторике как проблема менажа.; для коронных графов с 6, 8, 10, ... вершинами количество (ориентированных) гамильтоновых циклов равно

2, 12, 312, 9600, 416880, 23879520, 1749363840, ... (последовательность A094047 в OEIS )

Графы короны можно использовать, чтобы показать, что алгоритмы жадной раскраски плохо себя ведут в худшем случае: если вершины графа короны представлены алгоритму в порядке u ₀ , v ₀ , u ₁ , v ₁ и т. Д., То Для жадной раскраски используется n цветов, тогда как оптимальное количество цветов - два. Эта конструкция приписывается Джонсону (1974) ; графы короны иногда называют графами Джонсона с обозначением J _n . ^[6] Фюрер (1995) использует графы короны как часть конструкции, показывающей трудность аппроксимации задач раскраски.

Матушек (1996) использует расстояния в графах короны как пример метрического пространства , которое трудно встроить в нормированное векторное пространство .

Как показывают Miklavič & Potočnik (2003) , коронные графы являются одним из небольшого числа различных типов графов, которые могут встречаться как дистанционно регулярные циркулянтные графы .

Agarwal et al. (1994) описывают многоугольники, у которых есть графы короны как графы видимости ; они используют этот пример, чтобы показать, что представление графов видимости как объединение полных двудольных графов не всегда может быть эффективным с точки зрения пространства.

Граф короны с 2 n вершинами, ребра которого ориентированы от одной стороны двудольного раздела к другой, образует стандартный пример частично упорядоченного множества с порядковой размерностью  n .

Заметки [ править ]

Ссылки [ править ]

• Агарвал, Панкадж К .; Алон, Нога ; Аронов, Борис ; Сури, Субхаш (1994), "Can видимости графики быть представлены компактно?", Дискретные и Вычислительная геометрия , 12 (1): 347-365, DOI : 10.1007 / BF02574385 , МР  1298916.
• Архидиакон, Д .; Дебовский, М .; Dinitz, J .; Гавлас, Х. (2004), "Циклические системы в полном двудольном графе минус однофакторный", Дискретная математика , 284 (1–3): 37–43, DOI : 10.1016 / j.disc.2003.11.021 , MR  2071894.
• Чаудхари, Амитабх; Вишванатан, Сундар (2001), "Аппроксимация алгоритмы для ахроматического числа", журнал алгоритмов , 41 (2): 404-416, CiteSeerX  10.1.1.1.5562 , DOI : 10,1006 / jagm.2001.1192 , МР  1869259.
• де Кан, Доминик ; Грегори, Дэвид А .; Пуллман, Норман Дж. (1981), "Булев ранг матриц нуля или единицы", в Cadogan, Charles C. (ed.), Proc. 3-я Карибская конференция по комбинаторике и вычислениям , факультет математики Вест-Индского университета, стр. 169–173, MR  0657202.
• Эрдеш, Пол ; Симоновиц, Миклош (1980), «О хроматическом числе геометрических графов» (PDF) , Ars Combinatoria , 9 : 229–246, MR  0582295.
• Фюрер, Мартин (1995), "Улучшенные результаты определения твердости для аппроксимации хроматического числа", Proc. 36-я конференция IEEE Symp. Основы информатики и вычислительной техники (FOCS '95) , стр 414-421,. DOI : 10,1109 / SFCS.1995.492572 , ISBN 978-0-8186-7183-8.
• Джонсон, Д.С. (1974), "Наихудшее поведение алгоритмов раскраски графов", Proc. 5-я Юго-Восточная конф. по комбинаторике, теории графов и вычислениям, Utilitas Mathematicae , Winnipeg, pp. 513–527, MR  0389644
• Кубале, М. (2004), Раскраски графиков, Американское математическое общество, ISBN 978-0-8218-3458-9, MR  2074481
• Matoušek, Йиржи (1996), "О искажении необходимого для встраивания конечных метрических пространств в нормированные пространства", Израиль Журнал математики , 93 (1): 333-344, DOI : 10.1007 / BF02761110 , МР  1380650.
• Миклавич, Штефко; Potočnik, Primož (2003), "Дистанционно регулярные циркулянтами", Европейский журнал комбинаторике , 24 (7): 777-784, DOI : 10.1016 / S0195-6698 (03) 00117-3 , MR  2009391.

Внешние ссылки [ править ]

• Вайсштейн, Эрик В. «Граф короны» . MathWorld .