функция Бесселя
Функции Бесселя , впервые определенные математиком Даниэлем Бернулли , а затем обобщенные Фридрихом Бесселем , являются каноническими решениями y ( x ) дифференциального уравнения Бесселя
Наиболее важными являются случаи, когда является целым или полуцелым числом . Функции Бесселя для целых чисел также известны как цилиндрические функции или цилиндрические гармоники , потому что они появляются в решении уравнения Лапласа в цилиндрических координатах . Сферические функции Бесселя с полуцелым числом получаются при решении уравнения Гельмгольца в сферических координатах .


Функция Бесселя является обобщением функции синуса. Его можно интерпретировать как колебание струны с переменной толщиной, переменным натяжением (или обоими условиями одновременно); колебания в среде с переменными свойствами; колебания мембраны диска и др.
Уравнение Бесселя возникает при нахождении сепарабельных решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических или сферических координатах . Поэтому функции Бесселя особенно важны для многих задач распространения волн и статических потенциалов. При решении задач в цилиндрических системах координат получают функции Бесселя целого порядка ( α = n ); в сферических задачах получаются полуцелые порядки ( α = n + 1/2 ) . Например:
Функции Бесселя появляются и в других задачах, таких как обработка сигналов (например, см. FM-синтез звука , окно Кайзера или фильтр Бесселя ).
Поскольку это линейное дифференциальное уравнение второго порядка, должно быть два линейно независимых решения. Однако в зависимости от обстоятельств удобны различные составы этих растворов. Различные варианты приведены в таблице ниже и описаны в следующих разделах.

Функции Бесселя — это радиальная часть форм колебаний круглого
барабана .

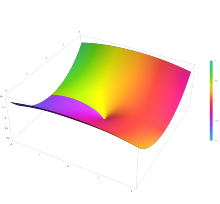
График функции Бесселя первого рода J n(z) с n=0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

График функции Бесселя первого рода
J α ( x ) для целых порядков
α = 0, 1, 2
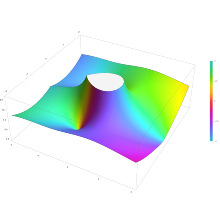
График функции Бесселя второго рода Y n(z) с n=0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

График функции Бесселя второго рода
Y α ( x ) для целых порядков
α = 0, 1, 2
График функции Ганкеля первого рода H n^(1)(z) с n=-0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

График функции Ганкеля второго рода H n^(2)(z) с n=-0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

Модифицированные функции Бесселя первого рода
I α ( x ) для
α = 0, 1, 2, 3
Модифицированные функции Бесселя второго рода
K α ( x ) для
α = 0, 1, 2, 3
График сферической функции Бесселя первого рода jn(z) с n=0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

График сферической функции Бесселя второго рода yn(z) с n=0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D
Сферические функции Бесселя первого рода
j n ( x ) для
n = 0, 1, 2 Сферические функции Бесселя второго рода,
y n ( x ) для
n = 0, 1, 2 График сферической функции Ганкеля первого рода hn^(1)(z) с n=-0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D
График сферической функции Ганкеля второго рода hn^(2)(z) с n=-0,5 в комплексной плоскости от -2-2i до 2+2i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D