Из Википедии, бесплатной энциклопедии
  (Перенаправлено из булевозначной функции )
Перейти к навигации Перейти к поиску
Бинарная схема решения и истина таблица тройной булевой функции
Не путать с двоичной функцией .

В математике и логике , А булева функция является функцией , чьи аргументы , а также сама функция, принимают значения из набора из двух элементов ( как правило , {0,1} или {True, False}). [1] [2] Альтернативное название - функция переключения , особенно часто используется в более ранней литературе по информатике . [3] [4] Булевы функции являются предметом булевой алгебры и теории переключений . [5]

Логическая функция принимает форму , которая называется логической областью и представляет собой неотрицательное целое число, называемое арностью функции. В случае , когда «функция» является постоянным элементом . Функция Логической с несколькими выходами, с представляет собой векторная или вектор- булева функция (ые S-окно в криптографии ). [6]

Существуют разные логические функции с аргументами; равно количеству различных таблиц истинности с записями.

Каждую -арную булеву функцию можно выразить как пропозициональную формулу в переменных , и две пропозициональные формулы логически эквивалентны тогда и только тогда, когда они выражают одну и ту же логическую функцию.

Примеры [ править ]

Диаграмма, отображающая шестнадцать двоичных логических функций
Шестнадцать двоичных булевых функций
См. Также: Таблица истинности

Элементарные симметричные булевы функции ( логические связки или логические элементы ):

  • НЕ , отрицание или дополнение - который получает один ввод и возвращает истину, когда этот ввод ложен («не»).
  • И или соединение - истина, когда все входные данные верны ("оба")
  • ИЛИ или дизъюнкция - истина, когда любой вход истинен ("либо")
  • XOR или исключительная дизъюнкция - истина, когда один из его входов истинен, а другой ложен ("не равно")
  • NAND или Sheffer stroke - истина, если не все входные данные верны ("не оба")
  • ИЛИ или логическое ни - истина, когда ни один из входов не является истиной ("ни один")
  • XNOR или логическое равенство - истина, когда оба входа одинаковы ("равны")

Примером более сложной функции является функция большинства (нечетного числа входов).

Представление [ править ]

Логическая функция, представленная в виде логической схемы

Логическая функция может быть указана разными способами:

  • Таблица истинности : явное перечисление ее значения для всех возможных значений аргументов
    • Диаграмма Маркуанда: значения таблицы истинности, расположенные в двумерной сетке (используется в карте Карно )
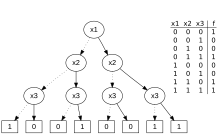
    • Диаграмма двоичных решений , в которой перечислены значения таблицы истинности в нижней части двоичного дерева
    • Диаграмма Венна , изображающая значения таблицы истинности в виде раскраски областей плоскости

Алгебраически, как пропозициональная формула с использованием рудиментарных булевых функций:

  • Нормальная форма отрицания , произвольное сочетание И и ИЛИ аргументов и их дополнений
  • Дизъюнктивная нормальная форма как ИЛИ аргументов и их дополнений
  • Конъюнктивная нормальная форма как ИЛИ аргументов и их дополнений
  • Каноническая нормальная форма , стандартизованная формула, однозначно определяющая функцию:
    • Алгебраическая нормальная форма или многочлен Жегалкина , как исключающее ИЛИ логических операций И ​​аргументов (дополнения не допускаются)
    • Полная (каноническая) дизъюнктивная нормальная форма , логическое ИЛИ, каждое из которых содержит каждый аргумент или дополнение ( minterms )
    • Полная (каноническая) конъюнктивная нормальная форма , логическое И или ИЛИ, каждое из которых содержит каждый аргумент или дополнение ( maxterms )
    • Каноническая форма Блейка , ИЛИ всех простых импликант функции

Булевы формулы также могут отображаться в виде графика:

  • Пропозиционально ориентированный ациклический граф
    • Цифровая принципиальная схема логических вентилей , логическая схема
    • График И-инвертора , использующий только И и НЕ

Для оптимизации электронных схем булевы формулы могут быть минимизированы с помощью алгоритма Куайна – Маккласки или карты Карно .

Анализ [ править ]

Свойства [ править ]

Логическая функция может иметь множество свойств: [7]

  • Константа : всегда истинно или всегда ложно независимо от аргументов.
  • Монотонный : для каждой комбинации значений аргументов изменение аргумента с false на true может привести только к переключению вывода с false на true, а не с true на false.
  • Линейный : для каждой переменной переворачивание значения переменной либо всегда влияет на значение истинности, либо никогда не имеет значения ( функция четности ).
  • Симметричный : значение не зависит от порядка его аргументов.
  • Однократное чтение : может быть выражено с помощью соединения , дизъюнкции и отрицания с одним экземпляром каждой переменной.
  • Сбалансированный : если его таблица истинности содержит равное количество нулей и единиц. Вес Хэмминга функции является число единиц в таблице истинности.
  • Бент : все его производные сбалансированы (спектр автокорреляции равен нулю)
  • Корреляция невосприимчива к m- му порядку: если выход не коррелирован со всеми (линейными) комбинациями не более m аргументов
  • Уклончиво : если оценка функции всегда требует значения всех аргументов
  • Логическая функция является функцией Шеффера, если ее можно использовать для создания (путем композиции) любой произвольной логической функции (см. Функциональную полноту )

Сложность схемы пытается классифицировать булевы функции по размеру или глубине схем, которые могут их вычислить.

Производные функции [ править ]

Булева функция может быть разложена с использованием теоремы Буля о разложении на положительные и отрицательные кофакторы Шеннона ( расширение Шеннона ), которые являются (k-1) -арными функциями, возникающими в результате фиксации одного из аргументов (до нуля или единицы). Общие (k-арные) функции, полученные путем наложения линейного ограничения на набор входных данных (линейное подпространство), называются подфункциями . [8]

Булевы производная функции к одному из аргументов является (к-1) -ичной функцией, верно , когда выход функции является чувствительным к выбранному входному переменному; это XOR двух соответствующих сомножителей. Производная и кофактор используются в разложении Рида – Мюллера . Эту концепцию можно обобщить как k-арную производную в направлении dx, полученную как разность (XOR) функции в x и x + dx. [8]

Криптографический анализ [ править ]

Преобразование Уолша булевой функции - это k-арная целочисленная функция, дающая коэффициенты разложения на линейные функции ( функции Уолша ), аналогичные разложению действительных функций на гармоники с помощью преобразования Фурье . Его квадрат - это спектр мощности или спектр Уолша . Коэффициент Уолша однобитового вектора является мерой корреляции этого бита с выходом булевой функции. Максимальный (по модулю) коэффициент Уолша известен как линейность функции. [8]Наибольшее количество битов (порядок), для которого все коэффициенты Уолша равны 0 (т. Е. Подфункции сбалансированы), называется отказоустойчивостью , а функция называется корреляционной невосприимчивой к этому порядку. [8] Коэффициенты Уолша играют ключевую роль в линейном криптоанализе .

Автокорреляции булевой функции является к-ичных целочисленная функция дает корреляцию между определенным набором изменений входов и функцией Ouput. Для данного битового вектора это связано с весом Хэмминга производной в этом направлении. Максимальный коэффициент автокорреляции (по абсолютной величине) известен как абсолютный показатель . [7] [8] Если все коэффициенты автокорреляции равны 0 (т. Е. Производные сбалансированы) для определенного числа битов, то говорят, что функция удовлетворяет критерию распространения в этом порядке; если все они равны нулю, то функция является бент-функцией . [9] Коэффициенты автокорреляции играют ключевую роль вдифференциальный криптоанализ .

Коэффициенты Уолша булевой функции и ее коэффициенты автокорреляции связаны эквивалентом теоремы Винера – Хинчина , которая утверждает, что автокорреляция и спектр мощности являются парой преобразования Уолша. [8]

Эти концепции можно естественным образом расширить до векторных булевых функций, рассматривая их выходные биты ( координаты ) по отдельности, или более тщательно, рассматривая набор всех линейных функций выходных битов, известных как его компоненты . [6] Набор преобразований Уолша компонентов известен как таблица линейного приближения (LAT) [10] [11] или корреляционная матрица [12] [13] ; он описывает корреляцию между различными линейными комбинациями входных и выходных битов. Набор коэффициентов автокорреляции компонентов представляет собой таблицу автокорреляции [11], связанный преобразованием Уолша компонентов [14] с более широко используемой таблицей распределения различий (DDT) [10] [11], в которой перечислены корреляции между различиями во входных и выходных битах (см. также: S-блок ).

Приложения [ править ]

Логические функции играют основную роль в вопросах теории сложности, а также при разработке процессоров для цифровых компьютеров , где они реализуются в электронных схемах с использованием логических вентилей .

Свойства булевых функций имеют решающее значение в криптографии , особенно при разработке алгоритмов с симметричным ключом (см. Блок подстановки ).

В теории кооперативных игр монотонные булевы функции называются простыми играми (играми с голосованием); это понятие применяется для решения проблем теории социального выбора .

См. Также [ править ]

  • Алгебра множеств
  • Булева алгебра
  • Темы булевой алгебры
  • Булево дифференциальное исчисление
  • Булевозначная функция
  • Модель дерева решений
  • Индикаторная функция
  • Логическая связка
  • Псевдобулева функция
  • Подписанный набор
  • Функция истины
  • Таблица истинности

Ссылки [ править ]

  1. ^ «Булева функция - Математическая энциклопедия» . encyclopediaofmath.org . Источник 2021-05-03 .
  2. ^ Вайсштейн, Эрик В. «Булева функция» . mathworld.wolfram.com . Источник 2021-05-03 .
  3. ^ "функция переключения" . TheFreeDictionary.com . Источник 2021-05-03 .
  4. ^ Дэвис, DW (декабрь 1957 г.). «Функции переключения трех переменных» . Операции IRE на электронных компьютерах . ИС-6 (4): 265–275. DOI : 10.1109 / TEC.1957.5222038 . ISSN 0367-9950 . 
  5. ^ Маккласки, Эдвард Дж. (01.01.2003), «Теория переключения» , Энциклопедия компьютерных наук , Великобритания: John Wiley and Sons Ltd., стр. 1727–1731, ISBN 978-0-470-86412-8, дата обращения 2021-05-03
  6. ^ a b Карлет, Клод. «Векторные булевы функции для криптографии» (PDF) . Парижский университет .
  7. ^ a b «Логические функции - Справочное руководство Sage 9.2: Криптография» . doc.sagemath.org . Проверено 1 мая 2021 .
  8. ^ a b c d e f Таранников Юрий; Королев, Петр; Ботев, Антон (2001). Бойд, Колин (ред.). «Коэффициенты автокорреляции и корреляционная невосприимчивость булевых функций» . Достижения в криптологии - ASIACRYPT 2001 . Конспект лекций по информатике. Берлин, Гейдельберг: Springer. 2248 : 460–479. DOI : 10.1007 / 3-540-45682-1_27 . ISBN 978-3-540-45682-7.
  9. ^ Канто, Анна; Карлет, Клод; Шарпен, Паскаль; Фонтейн, Кэролайн (2000-05-14). «Характеристики распространения и корреляционная невосприимчивость высоконелинейных булевых функций» . Материалы 19-й Международной конференции по теории и применению криптографических методов . EUROCRYPT'00. Брюгге, Бельгия: Springer-Verlag: 507–522. ISBN 978-3-540-67517-4.
  10. ^ a b Хейс, Ховард М. «Учебное пособие по линейному и дифференциальному криптоанализу» (PDF) .
  11. ^ a b c "S-блоки и их алгебраические представления - Справочное руководство Sage 9.2: Криптография" . doc.sagemath.org . Проверено 4 мая 2021 .
  12. ^ Daemen, Джоан; Говертс, Рене; Вандевалле, Джус (1995). Пренил, Барт (ред.). «Корреляционные матрицы» . Быстрое программное шифрование . Конспект лекций по информатике. Берлин, Гейдельберг: Springer: 275–285. DOI : 10.1007 / 3-540-60590-8_21 . ISBN 978-3-540-47809-6.
  13. ^ Daemen, Joan (10 июня 1998). «Глава 5: Распространение и корреляция - Приложение к предложению AES Rijndael» (PDF) . NIST .
  14. ↑ Ниберг, Кайса (1 декабря 2019 г.). "Расширенные таблицы автокорреляции и бумеранга и связи между свойствами нелинейности векторных булевых функций" (PDF) .

Дальнейшее чтение [ править ]

  • Крама, Ив; Хаммер, Питер Л. (2011), Булевы функции: теория, алгоритмы и приложения , Cambridge University Press, DOI : 10.1017 / CBO9780511852008 , ISBN 9780511852008 CS1 maint: обескураженный параметр ( ссылка )
  • "Булева функция" , Энциклопедия математики , EMS Press , 2001 [1994]
  • Янкович, Драган; Станкович, Радомир С .; Морага, Клаудио (ноябрь 2003 г.). «Оптимизация арифметических выражений с использованием свойства двойной полярности» (PDF) . Сербский журнал электротехники . 1 (71–80, номер 1): 71–80. DOI : 10.2298 / SJEE0301071J . Архивировано из оригинального (PDF) 05 марта 2016 года . Проверено 7 июня 2015 .
  • Арнольд, Брэдфорд Генри (1 января 2011 г.). Логика и булева алгебра . Курьерская корпорация. ISBN 978-0-486-48385-6.
  • Мано, ММ; Силетти, доктор медицины (2013), цифровой дизайн , Pearson