Преобразование данных (статистика)

Эта статья поднимает множество проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалить эти сообщения-шаблоны ) Эта статья требует дополнительных ссылок для проверки . Пожалуйста, помогите улучшить эту статью , добавив цитаты из надежных источников . Материал, не полученный от источника, может быть оспорен и удален. Найти источники:  статистика «Преобразование данных»  -  новости  · газеты  · книги  · ученый  · JSTOR ( сентябрь 2014 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения ) Этот раздел lede может быть слишком техническим, чтобы его могло понять большинство читателей . Пожалуйста, помогите улучшить его, чтобы он был понятен неспециалистам , не удаляя технических деталей. ( Август 2015 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения ) ( Узнайте, как и когда удалить этот шаблон сообщения )

Рассеивания , в котором области суверенных государств и зависимых территорий в мире построены на вертикальной оси против их популяций на горизонтальной оси. На верхнем графике используются необработанные данные. На нижнем графике данные о площади и населении были преобразованы с использованием функции логарифма.

В статистических данных , данные преобразования является применением детерминированной математической функции для каждой точки в данном наборе, то есть каждая точка данных г _я заменяется преобразованным значением у _я = е ( г _я ), где F является функцией. Преобразования обычно применяются для того, чтобы данные более точно соответствовали допущениям применяемой процедуры статистического вывода или для улучшения интерпретируемости или внешнего вида графиков .

Почти всегда функция, которая используется для преобразования данных, является обратимой и, как правило, непрерывной . Преобразование обычно применяется к набору сопоставимых измерений. Например, если мы работаем с данными о доходах людей в некоторой денежной единице, обычно значение дохода каждого человека преобразуется с помощью функции логарифма .

Мотивация [ править ]

Рекомендации относительно того, как данные должны быть преобразованы, или следует ли вообще применять преобразование, должны исходить из конкретного статистического анализа, который необходимо выполнить. Например, простой способ построить приблизительный 95% доверительный интервал для среднего значения генеральной совокупности состоит в том, чтобы взять среднее значение выборки плюс или минус две единицы стандартной ошибки . Однако используемый здесь постоянный коэффициент 2 является специфическим для нормального распределения и применим только в том случае, если выборочное среднее изменяется приблизительно нормально. В центральной предельной теореме гласит , что во многих ситуациях, выборочное среднее действительно изменяется , как правило , если размер выборки достаточно большой. Однако, если население существенно искаженои размер выборки самый умеренный, приближение, обеспечиваемое центральной предельной теоремой, может быть плохим, и полученный доверительный интервал, вероятно, будет иметь неверную вероятность охвата . Таким образом, когда есть свидетельства существенного перекоса в данных, принято преобразовывать данные в симметричное распределение ^[1] перед построением доверительного интервала. При желании доверительный интервал можно затем преобразовать обратно к исходной шкале, используя преобразование, обратное преобразованию, которое было применено к данным. ^{[2] [3]}

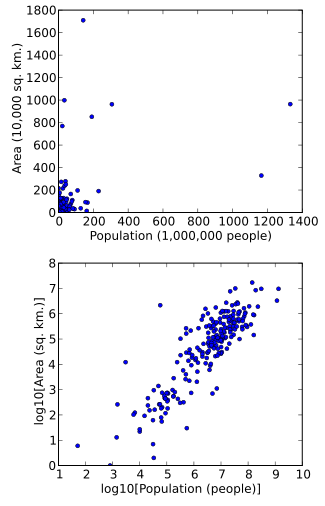
Данные также можно преобразовать, чтобы упростить их визуализацию. Например, предположим, что у нас есть диаграмма рассеяния, на которой точки - это страны мира, а отображаемые значения данных - это площадь суши и население каждой страны. Если график построен с использованием нетрансформированных данных (например, квадратных километров для площади и количества людей для населения), большинство стран будут нанесены на график в виде плотной группы точек в нижнем левом углу графика. Несколько стран с очень большими территориями и / или населением будут рассредоточены по большей части площади графика. Простое изменение масштаба единиц (например, до тысяч квадратных километров или миллионов людей) этого не изменит. Однако после логарифмической трансформации как площади, так и населения, точки будут более равномерно распределены на графике.

Другой причиной применения преобразования данных является улучшение интерпретируемости, даже если не требуется выполнять формальный статистический анализ или визуализацию. Например, предположим, что мы сравниваем автомобили с точки зрения их экономии топлива. Эти данные обычно представлены в виде «километров на литр» или «миль на галлон». Однако, если цель состоит в том, чтобы оценить, сколько дополнительного топлива человек использовал бы в течение одного года при вождении одного автомобиля по сравнению с другим, более естественно работать с данными, преобразованными с помощью обратной функции , давая литры на километр или галлоны. за милю.

В регрессе [ править ]

Преобразование данных может использоваться в качестве лечебной меры, чтобы сделать данные подходящими для моделирования с помощью линейной регрессии, если исходные данные нарушают одно или несколько предположений линейной регрессии. ^[4] Например, простейшие линейные модели регрессий предполагают линейную зависимость между ожидаемым значением из Y (в переменном отклик , чтобы быть предсказана) и каждым независимым переменным (когда другие независимыми переменными удерживаются фиксированными). Если линейность не соблюдается даже приблизительно, иногда можно преобразовать независимые или зависимые переменные в регрессионной модели для улучшения линейности. ^[5]Например, добавление квадратичных функций исходных независимых переменных может привести к линейной зависимости с ожидаемым значением из Y, что приводит к полиномиальной регрессии модели, частный случай линейной регрессии.

Другое предположением линейной регрессии является гомоскедастичностью , то есть дисперсия из ошибок должна быть одинаковой , независимо от значений предикторов. Если это предположение нарушается (т. Е. Если данные гетероскедастичны ), может оказаться возможным найти преобразование только Y или преобразования как X ( переменных-предикторов ), так и Y , так что предположение гомоскедастичности (в дополнение к линейности предположение) верно для преобразованных переменных ^[5], и поэтому к ним может применяться линейная регрессия.

Еще одно применение преобразования данных - решить проблему отсутствия нормальности с точки зрения ошибок. Одномерная нормальность не требуется для оценки параметров регрессии методом наименьших квадратов (см. Теорему Гаусса – Маркова ). Однако доверительные интервалы и тесты гипотез будут иметь лучшие статистические свойства, если переменные демонстрируют многомерную нормальность . Преобразования, которые стабилизируют дисперсию членов ошибки (т. Е. Те, которые обращаются к гетероскедатичности), часто также помогают сделать условия ошибки приблизительно нормальными. ^{[5] [6]}

Примеры [ править ]

Уравнение:${\ displaystyle Y = a + bX}$

Значение: увеличение X на единицу связано с увеличением Y в среднем на b единиц.

Уравнение:             (Из потенцируя обе части уравнения: )${\ Displaystyle \ журнал (Y) = а + bX}$${\displaystyle Y=e^{a}e^{bX}}$

Значение: увеличение X на единицу связано со средним увеличением на b единиц , или, что эквивалентно, Y увеличивается в среднем на мультипликативный коэффициент . В иллюстративных целях, если бы вместо натурального логарифма в приведенном выше преобразовании использовался логарифм с основанием 10 и те же символы ( a и b ) использовались для обозначения коэффициентов регрессии, то увеличение на единицу X привело бы к увеличению Y в раз. в среднем. Если бы b было 1, то это означает 10-кратное увеличение Y для увеличения X на единицу.${\displaystyle \log(Y)}$${\displaystyle e^{b}\!}$${\displaystyle 10^{b}}$

Уравнение:${\displaystyle Y=a+b\log(X)}$

Значение: k-кратное увеличение X связано со средним увеличением единиц в Y. Для наглядности, если в приведенном выше преобразовании использовался логарифм по основанию 10 вместо натурального логарифма и использовались те же символы ( a и b ) чтобы обозначить коэффициенты регрессии, то десятикратное увеличение X приведет к среднему увеличению единиц в Y${\displaystyle b\times \log(k)}$${\displaystyle b\times \log _{10}(10)=b}$

Уравнение:       (Из потенцируя обе части уравнения: )${\displaystyle \log(Y)=a+b\log(X)}$${\displaystyle Y=e^{a}X^{b}}$

Значение: увеличение X в k раз связано с мультипликативным увеличением Y в среднем. Таким образом, если X удвоится, это приведет к изменению Y на мультипликативный коэффициент . ^[7]${\displaystyle k^{b}}$${\displaystyle 2^{b}\!}$

Альтернатива [ править ]

Обобщенные линейные модели (GLM) обеспечивают гибкое обобщение обычной линейной регрессии, которое позволяет использовать переменные отклика, которые имеют модели распределения ошибок, отличные от нормального распределения. GLM позволяют связать линейную модель с переменной отклика через функцию связи и позволяют величине дисперсии каждого измерения быть функцией его прогнозируемого значения. ^{[8] [9]}

Общие случаи [ править ]

Преобразования логарифма и квадратного корня обычно используются для положительных данных, а мультипликативное обратное (обратное) преобразование может использоваться для ненулевых данных. Преобразование мощности - это семейство преобразований, параметризованное неотрицательным значением λ, которое включает в себя логарифм, квадратный корень и мультипликативную обратную величину как особые случаи. Чтобы подойти к преобразованию данных систематически, можно использовать статистическую оценку.методы для оценки параметра λ в преобразовании мощности, тем самым идентифицируя преобразование, которое является приблизительно наиболее подходящим в данной настройке. Поскольку семейство степенных преобразований также включает в себя преобразование идентичности, этот подход также может указать, лучше ли анализировать данные без преобразования. В регрессионном анализе этот подход известен как метод Бокса – Кокса .

Обратное преобразование, некоторые преобразования мощности, такие как преобразование Йео – Джонсона, и некоторые другие преобразования, такие как применение обратного гиперболического синуса , могут быть осмысленно применены к данным, которые включают как положительные, так и отрицательные значения ^[10] (преобразование мощности обратимо по все действительные числа, если λ - нечетное целое число). Однако, когда наблюдаются как отрицательные, так и положительные значения, иногда обычно начинают с добавления константы ко всем значениям, создавая набор неотрицательных данных, к которым может быть применено любое преобразование мощности. ^[3]

Обычная ситуация, когда применяется преобразование данных, - это когда интересующее значение колеблется в пределах нескольких порядков . Многие физические и социальные явления демонстрируют такое поведение - доходы, популяции видов, размеры галактик и количество осадков, и это лишь некоторые из них. Преобразования мощности, в частности логарифм, часто можно использовать для создания симметрии в таких данных. Часто предпочитают логарифм, потому что его результат легко интерпретировать в терминах «кратных изменений».

Логарифм также оказывает полезное влияние на отношения. Если мы сравниваем положительные величины X и Y с использованием отношения X  /  Y , то, если X  <  Y , соотношение находится в интервале (0,1), тогда как если X  >  Y , соотношение находится в полупрямой (1 , ∞), где отношение 1 соответствует равенству. В анализе, где X и Y обрабатываются симметрично, логарифм log ( X  /  Y ) равен нулю в случае равенства, и он обладает тем свойством, что если X в K раз больше, чем Y, логарифмическое отношение равноудалено от нуля, как в ситуации, когда Y в K раз больше, чем X (логарифмические отношения равны log ( K ) и -log ( K ) в этих двух ситуациях).

Если значения естественным образом ограничены диапазоном от 0 до 1, не включая конечные точки, тогда может быть подходящим логит-преобразование : это дает значения в диапазоне (−∞, ∞).

Превращение в нормальность [ править ]

1. Не всегда необходимо или желательно преобразовывать набор данных, чтобы он напоминал нормальное распределение. Однако, если требуется симметрия или нормальность, их часто можно вызвать с помощью одного из степенных преобразований.

2. Лингвистическая степенная функция распределяется по закону Ципфа-Мандельброта . Распределение является чрезвычайно резким и лептокуртичным , поэтому исследователям пришлось отказаться от статистики для решения, например, проблем с установлением авторства . Тем не менее, использование гауссовой статистики вполне возможно при применении преобразования данных. ^[11]

3. Чтобы оценить, была ли достигнута нормальность после преобразования, можно использовать любой из стандартных тестов на нормальность . Графический подход обычно более информативен, чем формальный статистический тест, и, следовательно, нормальный график квантилей обычно используется для оценки соответствия набора данных нормальной совокупности. В качестве альтернативы также были предложены практические правила, основанные на асимметрии и эксцессе выборки . ^{[12] [13]}

Переход к равномерному или произвольному распределению [ править ]

Если мы наблюдаем набор из n значений X ₁ , ..., X _n без связей (т. Е. Существует n различных значений), мы можем заменить X _i преобразованным значением Y _i = k , где k определено таким образом, что X _i - k- ^{е по} величине среди всех значений X. Это называется ранг преобразование , ^[14] и создает данные с идеальной подгонкой к равномерному распределению . У этого подхода есть популяционный аналог.

Использование вероятностей интегрального преобразования , если Х является любой случайной величиной , а Р представляет собой интегральную функцию распределения по X , то до тех пор , как Р обратим, случайная величина U = F ( X ) следует равномерное распределение на единичный интервал [0 , 1].

От равномерного распределения мы можем перейти к любому распределению с обратимой кумулятивной функцией распределения. Если G - обратимая кумулятивная функция распределения, а U - равномерно распределенная случайная величина, то случайная величина G ^-1 ( U ) имеет G в качестве кумулятивной функции распределения.

Если сложить их вместе, если X - любая случайная величина, F - обратимая кумулятивная функция распределения X , а G - обратимая кумулятивная функция распределения, то случайная величина G ⁻¹ ( F ( X )) имеет G в качестве кумулятивной функции распределения. .

Преобразования, стабилизирующие дисперсию [ править ]

Многие типы статистических данных демонстрируют «отношение дисперсии к среднему», что означает, что изменчивость различна для значений данных с разными ожидаемыми значениями . Например, при сравнении различных групп населения в мире разница в доходе имеет тенденцию увеличиваться со средним доходом. Если мы рассмотрим несколько небольших территориальных единиц (например, округа в Соединенных Штатах) и получим среднее значение и дисперсию доходов в каждом округе, обычно округа с более высоким средним доходом также имеют более высокие отклонения.

Дисперсия стабилизирующих преобразований целей , чтобы удалить дисперсию-на-среднего отношение, так что дисперсия становится постоянная относительно среднего. Примерами преобразований, стабилизирующих дисперсию, являются преобразование Фишера для выборочного коэффициента корреляции, преобразование квадратного корня или преобразование Анскомба для данных Пуассона (данные подсчета), преобразование Бокса – Кокса для регрессионного анализа и преобразование квадратного корня арксинуса или угловое преобразование для пропорции ( биномиальные данные). Хотя обычно используется для статистического анализа пропорциональных данных, преобразование квадратного корня арксинуса не рекомендуется, посколькулогистическая регрессия или логит-преобразование более подходят для биномиальных или небиномиальных пропорций, соответственно, особенно из-за уменьшения ошибки типа II . ^{[15] [3]}

Преобразования для многомерных данных [ править ]

Одномерные функции могут применяться точечно к многомерным данным для изменения их предельных распределений. Также возможно изменить некоторые атрибуты многомерного распределения, используя соответствующим образом сконструированное преобразование. Например, при работе с временными рядами и другими типами последовательных данных обычно различают данные для улучшения стационарности . Если данные, сгенерированные случайным вектором X , наблюдаются как векторы X _i наблюдений с ковариационной матрицей Σ, для декорреляции данных можно использовать линейное преобразование . Для этого используется разложение Холецкого, чтобы выразить Σ = A А ' . Тогда преобразованный вектор Y _i = A ⁻¹ X _i имеет единичную матрицу в качестве своей ковариационной матрицы.

См. Также [ править ]

• Arcsin
• Функциональная инженерия
• Logit
• Нелинейная регрессия # Преобразование
• Коэффициент корреляции Пирсона
• Преобразование мощности (Бокс – Кокс)

Ссылки [ править ]

Внешние ссылки [ править ]

• Преобразования журналов для асимметричных и широких распределений - обсуждение преобразований журнала и «знакового логарифма» (глава из «Практическая наука о данных с R»).