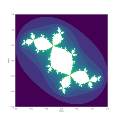
Кролик дуади

Кролик Дуади является любым из различной конкретной заполненной Жюлиа , связанной с параметром вблизи центра периода 3 почки Мандельброта набора для комплексного квадратичного отображения .

• 

  цвета показывают итерации

• 

  Уровни серого указывают на скорость сходимости к бесконечности или к привлекательному циклу.

• 

  границы наборов уровней

• 

  толстый кролик

• 

  с позвоночником

• 

  внешние лучи попадают в фиксированную точку${\ Displaystyle \ альфа _ {с} \,}$ .

• 

  Возмущенный кролик ^[1]

• 

  Возмущенный кролик зум

Имя [ редактировать ]

Кролик Дуади или кролик Дуади назван в честь французского математика Адриана Дуади . ^[2]

Жир кролик кролик или пухлый имеет гр в корне 1 / 3- конечности от множества Мандельброта . Он имеет параболическую фиксированную точку с 3 лепестками . ^[3]

Формы комплексного квадратичного отображения [ править ]

Есть две общие формы для комплексного квадратичного отображения . Первая, также называемая сложной логистической картой , записывается как${\ Displaystyle {\ mathcal {M}}}$

${\displaystyle z_{n+1}={\mathcal {M}}z_{n}=\gamma z_{n}\left(1-z_{n}\right),}$

где - комплексная переменная и - комплексный параметр. Вторая распространенная форма - это${\displaystyle z}$${\displaystyle \gamma }$

${\displaystyle w_{n+1}={\mathcal {M}}w_{n}=w_{n}^{2}-\mu .}$

Вот комплексная переменная и комплексный параметр. Переменные и связаны уравнением${\displaystyle w}$${\displaystyle \mu }$${\displaystyle z}$${\displaystyle w}$

${\displaystyle z=-{\frac {w}{\gamma }}+{\frac {1}{2}},}$

а параметры и связаны уравнениями${\displaystyle \gamma }$${\displaystyle \mu }$

${\displaystyle \mu =\left({\frac {\gamma -1}{2}}\right)^{2}-{\frac {1}{4}}\quad ,\quad \gamma =1\pm {\sqrt {1+4\mu }}.}$

Обратите внимание, что это инвариантно относительно замены .${\displaystyle \mu }$${\displaystyle \gamma \to 2-\gamma }$

Мандельброт и заполненные множества Жюлиа [ править ]

Есть две плоскости, связанные с . Одна из них, (или ) плоскость, будет называться плоскостью отображения , поскольку отправляет эту плоскость в себя. Другой, плоскость (или ), мы будем называть плоскостью управления.${\displaystyle {\mathcal {M}}}$${\displaystyle z}$${\displaystyle w}$${\displaystyle {\mathcal {M}}}$${\displaystyle \gamma }$${\displaystyle \mu }$

Характер того, что происходит в плоскости отображения при многократном применении, зависит от того, где (или ) находится в плоскости управления. Заполнена Жюлиа состоит из всех точек плоскости отображения, образа остаются ограниченными при неограниченно повторных применениях . Множество Мандельброта состоит из тех точек , в контрольной плоскости, что связано заполненный Жюлиа в отображении плоскости связно.${\displaystyle {\mathcal {M}}}$${\displaystyle \gamma }$${\displaystyle \mu }$${\displaystyle {\mathcal {M}}}$

На рисунке 1 показано множество Мандельброта, когда является управляющим параметром, а на рисунке 2 показано множество Мандельброта, когда является управляющим параметром. Поскольку и являются аффинными преобразованиями друг друга (линейное преобразование плюс перенос), заполненные множества Жюлиа выглядят почти одинаково в плоскостях или .${\displaystyle \gamma }$${\displaystyle \mu }$${\displaystyle z}$${\displaystyle w}$${\displaystyle z}$${\displaystyle w}$

Рисунок 2: Набор Мандельброта на плоскости.${\displaystyle \mu }$

Кролик Дуади [ править ]

^{[ требуется разъяснение ]}

Кролик Дуади в экспоненциальной семье

Кролика Дуади проще всего описать с помощью набора Мандельброта, как показано на рисунке 1 (выше). На этом рисунке набор Мандельброта, по крайней мере, если смотреть с расстояния, выглядит как два соединенных спиной к спине единичных дисков с отростками. Рассмотрим ростки в положениях 1 и 5 часов на правом диске или ростки в положениях 7 и 11 часов на левом диске. Когда он находится внутри одного из этих четырех отростков, связанный заполненный набор Джулии на плоскости отображения является кроликом Дуади. Для этих значений можно показать, что имеется и еще одна точка как неустойчивые (отталкивающие) фиксированные точки и как притягивающая фиксированная точка. Кроме того, на карте есть три притягивающие неподвижные точки. Кролик Дуади состоит из трех притягивающих неподвижных точек.${\displaystyle \gamma }$${\displaystyle \gamma }$${\displaystyle {\mathcal {M}}}$${\displaystyle z=0}$${\displaystyle z=\infty }$${\displaystyle {\mathcal {M}}^{3}}$${\displaystyle z_{1}}$, И и их бассейны притяжения.${\displaystyle z_{2}}$${\displaystyle z_{3}}$

Например, на рис. 3 кролик Дуади показан в плоскости, когда точка в пятичасовом ростке правого диска. Для этого значения карта имеет фиксированные точки отталкивания и . Три притягивающие фиксированные точки (также называемые фиксированными точками периода три) имеют положения${\displaystyle z}$${\displaystyle \gamma =\gamma _{D}=2.55268-0.959456i}$${\displaystyle \gamma }$${\displaystyle {\mathcal {M}}}$${\displaystyle z=0}$${\displaystyle z=.656747-.129015i}$${\displaystyle {\mathcal {M}}^{3}}$

${\displaystyle z^{1}=0.499997032420304-(1.221880225696050\times 10^{-6})i{\;}{\;}{\mathrm {(red)} },}$

${\displaystyle z^{2}=0.638169999974373-(0.239864000011495)i{\;}{\;}{\mathrm {(green)} },}$

${\displaystyle z^{3}=0.799901291393262-(0.107547238170383)i{\;}{\;}{\mathrm {(yellow)} }.}$

Красный, зеленый, желтый и точки лежат в бассейнах , и из , соответственно. Белые точки лежат в бассейне с .${\displaystyle B(z^{1})}$${\displaystyle B(z^{2})}$${\displaystyle B(z^{3})}$${\displaystyle {\mathcal {M}}^{3}}$${\displaystyle B(\infty )}$${\displaystyle {\mathcal {M}}}$

Действие на эти неподвижные точки задается соотношениями${\displaystyle {\mathcal {M}}}$

${\displaystyle {\mathcal {M}}z^{1}=z^{2},}$

${\displaystyle {\mathcal {M}}z^{2}=z^{3},}$

${\displaystyle {\mathcal {M}}z^{3}=z^{1}.}$

Этим соотношениям соответствуют результаты

${\displaystyle {\mathcal {M}}B(z^{1})=B(z^{2}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {red} }\subseteq {\mathrm {green} },}$

${\displaystyle {\mathcal {M}}B(z^{2})=B(z^{3}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {green} }\subseteq {\mathrm {yellow} },}$

${\displaystyle {\mathcal {M}}B(z^{3})=B(z^{1}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {yellow} }\subseteq {\mathrm {red} }.}$

Обратите внимание на чудесную фрактальную структуру на границах бассейна.

Рисунок 3: кролик Дуади для или .${\displaystyle \gamma =2.55268-0.959456i}$${\displaystyle \mu =0.122565-0.744864i}$

В качестве второго примера на рисунке 4 показан кролик Дуади, когда точка в одиннадцатичасовом ростке на левом диске. (Как отмечалось ранее, инвариантен относительно этого преобразования.) Кролик теперь сидит на странице более симметрично. Фиксированные точки периода три расположены в${\displaystyle \gamma =2-\gamma _{D}=-.55268+.959456i}$${\displaystyle \mu }$

${\displaystyle z^{1}=0.500003730675024+(6.968273875812428\times 10^{-6})i{\;}{\;}({\mathrm {red} }),}$

${\displaystyle z^{2}=-0.138169999969259+(0.239864000061970)i{\;}{\;}({\mathrm {green} }),}$

${\displaystyle z^{3}=-0.238618870661709-(0.264884797354373)i{\;}{\;}({\mathrm {yellow} }),}$

Собственно отталкивающие неподвижные точки расположены в точках и . Три главных лепестка слева, которые содержат фиксированные точки с периодом три , и , встречаются в фиксированной точке , а их двойники справа встречаются в этой точке . Можно показать, что влияние на точки около начала координат состоит из вращения против часовой стрелки вокруг начала координат или почти с последующим масштабированием (растяжением) с коэффициентом .${\displaystyle {\mathcal {M}}}$${\displaystyle z=0}$${\displaystyle z=1.450795+0.7825835i}$${\displaystyle z^{1}}$${\displaystyle z^{2}}$${\displaystyle z^{3}}$${\displaystyle z=0}$${\displaystyle z=1}$${\displaystyle {\mathcal {M}}}$${\displaystyle \arg(\gamma )}$${\displaystyle 120^{\circ }}$${\displaystyle |\gamma |=1.1072538}$

Рисунок 4: кролик Дуади для или .${\displaystyle \gamma =-0.55268+0.959456i}$${\displaystyle \mu =0.122565-0.744864i}$

См. Также [ править ]

• Кривая дракона
• Кольцо Германа
• Диск Зигеля
• Проблема скрученного кролика ^{[4] [ почему? ]}

Ссылки [ править ]

Внешние ссылки [ править ]

• Вайсштейн, Эрик В. "Фрактал кролика Дуади" . MathWorld .
• Драгт, А. http://www.physics.umd.edu/dsat/dsatliemethods.html . Методы Ли для нелинейной динамики с приложениями к физике ускорителей .

Эта статья включает материал из Douady Rabbit на PlanetMath , который находится под лицензией Creative Commons Attribution / Share-Alike License .