Взвешивание обратных расстояний

Обратное расстояние весового ( IDW ) представляет собой тип детерминированного метода для многомерной интерполяции с известным рассеянным множеством точек. Присвоенные значения неизвестным точкам вычисляются со средневзвешенным значением значений, доступных в известных точках.

Название, данное этому типу методов, было мотивировано примененным средневзвешенным значением , поскольку при присвоении весов он обращается к обратному расстоянию до каждой известной точки («степень близости»).

Определение проблемы [ править ]

Ожидаемый результат - дискретное присвоение неизвестной функции в исследуемой области:${\ displaystyle u}$

${\ displaystyle u (x): x \ to \ mathbb {R}, \ quad x \ in \ mathbf {D} \ subset \ mathbb {R} ^ {n},}$

где исследуемый регион.${\ displaystyle \ mathbf {D}}$

Набор известных точек данных можно описать как список кортежей :${\ displaystyle N}$

${\ displaystyle [(x_ {1}, u_ {1}), (x_ {2}, u_ {2}), ..., (x_ {N}, u_ {N})].}$

Функция должна быть «плавной» (непрерывной и однократно дифференцируемой), а точнее ( ) и соответствовать интуитивным ожиданиям пользователя в отношении исследуемого явления. Кроме того, функция должна подходить для компьютерного приложения по разумной цене (в настоящее время базовая реализация, вероятно, будет использовать параллельные ресурсы ).${\ Displaystyle и (х_ {я}) = и_ {я}}$

Метод Шепарда [ править ]

Историческая справка [ править ]

В Гарвардской лаборатории компьютерной графики и пространственного анализа с 1965 года собрались разные ученые, чтобы переосмыслить, среди прочего, то, что мы сейчас называем географическими информационными системами . ^[1]

Движущая сила лаборатории, Говард Фишер, задумал улучшенную программу компьютерного картографирования, которую он назвал SYMAP, которую с самого начала Фишер хотел улучшить в интерполяции. Он показал первокурсникам Гарвардского колледжа свою работу над SYMAP, и многие из них участвовали в лабораторных мероприятиях. Один первокурсник, Дональд Шепард, решил пересмотреть интерполяцию в SYMAP, результатом чего стала его знаменитая статья 1968 года ^[2].

На алгоритм Шепарда также повлиял теоретический подход Уильяма Варнца и других сотрудников лаборатории, которые работали с пространственным анализом. Он провел ряд экспериментов с показателем расстояния, выбрав что-то более близкое к модели гравитации (показатель -2). Шепард реализовал не только базовое взвешивание обратных расстояний, но также разрешил интерполяцию барьеров (проницаемых и абсолютных).

В то время над интерполяцией работали другие исследовательские центры, в частности Университет Канзаса и их программа SURFACE II. Тем не менее, возможности SYMAP были самыми современными, даже несмотря на то, что они были запрограммированы студентом.

Основная форма [ править ]

Интерполяция Шепарда для различных параметров мощности p по разрозненным точкам на поверхности${\displaystyle z=\exp(-x^{2}-y^{2})}$

Общая форма поиска интерполированного значения в заданной точке на основе выборок для использования IDW - это интерполирующая функция:${\displaystyle u}$${\displaystyle x}$${\displaystyle u_{i}=u(x_{i})}$${\displaystyle i=1,2,...,N}$

${\displaystyle u(\mathbf {x} )={\begin{cases}{\dfrac {\sum _{i=1}^{N}{w_{i}(\mathbf {x} )u_{i}}}{\sum _{i=1}^{N}{w_{i}(\mathbf {x} )}}},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})\neq 0{\text{ for all }}i,\\u_{i},&{\text{if }}d(\mathbf {x} ,\mathbf {x} _{i})=0{\text{ for some }}i,\end{cases}}}$

где

${\displaystyle w_{i}(\mathbf {x} )={\frac {1}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}}$

является простой весовой функцией IDW, как определено Шепардом, ^[2] x обозначает интерполированную (произвольную) точку, x _i является интерполирующей (известной) точкой, является заданным расстоянием ( метрическим оператором) от известной точки x _i до неизвестная точка x , N - общее количество известных точек, используемых при интерполяции, и является положительным вещественным числом, называемым параметром мощности.${\displaystyle d}$${\displaystyle p}$

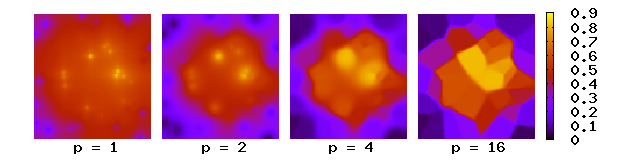
Здесь вес уменьшается по мере увеличения расстояния от интерполированных точек. Большие значения присваивают большее влияние значениям, ближайшим к интерполированной точке, в результате чего получается мозаика плиток ( диаграмма Вороного ) с почти постоянным интерполированным значением для больших значений p . Для двух измерений параметры мощности приводят к тому, что в интерполированных значениях преобладают удаленные точки, поскольку при плотности точек данных и соседних точек между расстояниями до , суммарный вес приблизительно равен${\displaystyle p}$${\displaystyle p\leq 2}$${\displaystyle \rho }$${\displaystyle r_{0}}$${\displaystyle R}$

${\displaystyle \sum _{j}w_{j}\approx \int _{r_{0}}^{R}{\frac {2\pi r\rho \,dr}{r^{p}}}=2\pi \rho \int _{r_{0}}^{R}r^{1-p}\,dr,}$

который расходится при и . Для размеров M то же самое справедливо и для . Для выбора значения p можно учитывать желаемую степень сглаживания при интерполяции, плотность и распределение интерполируемых отсчетов, а также максимальное расстояние, на котором отдельному отсчету разрешено влиять на окружающие.${\displaystyle R\rightarrow \infty }$${\displaystyle p\leq 2}$${\displaystyle p\leq M}$

Метод Шепарда является следствием минимизации функционала, связанного с мерой отклонений между наборами интерполируемых точек { x , u } и i наборами интерполированных точек { x _i , u _i }, определяемых как:

${\displaystyle \phi (\mathbf {x} ,u)=\left(\sum _{i=0}^{N}{\frac {(u-u_{i})^{2}}{d(\mathbf {x} ,\mathbf {x} _{i})^{p}}}\right)^{\frac {1}{p}},}$

выводится из условия минимизации:

${\displaystyle {\frac {\partial \phi (\mathbf {x} ,u)}{\partial u}}=0.}$

Метод может быть легко распространен на другие размерные пространства, и фактически он является обобщением приближения Лагранжа на многомерные пространства. Модифицированная версия алгоритма, предназначенная для трехвариантной интерполяции, была разработана Робертом Дж. Ренка и доступна в Netlib как алгоритм 661 в библиотеке toms.

Пример в одном измерении [ править ]

Интерполяция Шепарда в одном измерении, по 4 разрозненным точкам и с использованием p = 2

Метрика Лукашика – Кармовского [ править ]

Еще одна модификация метода Шепарда была предложена Лукашиком ^[3] также в приложениях к экспериментальной механике. Предлагаемая весовая функция имела вид

${\displaystyle w_{k}(\mathbf {x} )={\frac {1}{(D_{**}(\mathbf {x} ,\mathbf {x} _{k}))^{\frac {1}{2}}}},}$

где - метрика Лукашика – Кармовского, выбранная также с учетом распределений вероятностей статистической ошибки измерения интерполированных точек.${\displaystyle D_{**}(\mathbf {x} ,\mathbf {x} _{k})}$

Модифицированный метод Шепарда [ править ]

Другая модификация метода Шепарда вычисляет интерполированное значение, используя только ближайших соседей в R- сфере (вместо полной выборки). В этом случае веса немного изменены:

${\displaystyle w_{k}(\mathbf {x} )=\left({\frac {\max(0,R-d(\mathbf {x} ,\mathbf {x} _{k}))}{Rd(\mathbf {x} ,\mathbf {x} _{k})}}\right)^{2}.}$

В сочетании с быстрой структурой пространственного поиска (например, kd-tree ) он становится эффективным методом интерполяции N log N, подходящим для крупномасштабных задач.

Ссылки [ править ]

См. Также [ править ]

• Многомерная интерполяция
• Оценка плотности ядра