Статистика заказов

В статистике , то к - го порядка статистики из статистической выборки равна его к м-наименьшее значение. ^[1] Вместе со статистикой рангов, статистика заказов является одним из самых фундаментальных инструментов непараметрической статистики и вывода .

Важными частными случаями упорядоченной статистики являются минимальное и максимальное значение выборки и (с некоторыми оговорками, обсуждаемыми ниже) медиана выборки и другие квантили выборки .

При использовании теории вероятностей для анализа порядковой статистики случайных выборок из непрерывного распределения , кумулятивная функция распределения используется для сведения анализа к случаю порядковой статистики равномерного распределения .

Обозначения и примеры [ править ]

Например, предположим, что наблюдаются или записываются четыре числа, в результате чего получается выборка размером 4. Если значения выборки равны

6, 9, 3, 8,

статистика заказа будет обозначена

${\ Displaystyle х _ {(1)} = 3, \ \ x _ {(2)} = 6, \ \ x _ {(3)} = 8, \ \ x _ {(4)} = 9, \,}$

где нижний индекс ( i ) в круглых скобках указывает статистику i- го порядка выборки.

Первого порядка статистики (или наименьший порядок статистики ) всегда является минимальной выборки, то есть,

${\ Displaystyle X _ {(1)} = \ мин \ {\, X_ {1}, \ ldots, X_ {n} \, \}}$

где, следуя общепринятому соглашению, мы используем прописные буквы для обозначения случайных величин и строчные буквы (как указано выше) для обозначения их фактических наблюдаемых значений.

Аналогичным образом , для образца размера п , то п - го порядка статистика ( , или по величине статистика порядка ) является максимумом , то есть

${\ Displaystyle X _ {(n)} = \ max \ {\, X_ {1}, \ ldots, X_ {n} \, \}.}$

Диапазон выборки - это разница между максимумом и минимумом. Это функция статистики заказов:

${\ displaystyle {\ rm {Range}} \ {\, X_ {1}, \ ldots, X_ {n} \, \} = X _ {(n)} - X _ {(1)}.}$

Аналогичная важная статистика в исследовательском анализе данных, которая просто связана со статистикой порядка, - это межквартильный диапазон выборки .

Медиана выборки может быть, а может и не быть статистикой порядка, поскольку есть одно среднее значение только тогда, когда число n наблюдений нечетное . Точнее, если n = 2 m +1 для некоторого целого числа m , то медиана выборки является статистикой порядка. С другой стороны, когда п является даже , п = 2 м , и есть две средних значений, и , и образец медиана некоторая функция из двух (обычно в среднем) и , следовательно , не приказ статистики. Аналогичные замечания применимы ко всем квантилям выборки.${\ Displaystyle X _ {(м + 1)}}$${\ Displaystyle X _ {(м)}}$${\ Displaystyle X _ {(м + 1)}}$

Вероятностный анализ [ править ]

Для любых случайных величин X ₁ , X ₂ ..., X _n , порядковые статистики X ₍₁₎ , X ₍₂₎ , ..., X _{( n )} также являются случайными величинами, определяемыми путем сортировки значений ( реализаций ) из X ₁ , ..., X _п в порядке возрастания.

Когда случайные величины X ₁ , X ₂ ..., X _n образуют выборку, они независимы и одинаково распределены . Этот случай рассматривается ниже. Как правило, случайные величины X ₁ , ..., X _n могут возникать в результате выборки из более чем одной совокупности. Тогда они независимы , но не обязательно одинаково распределены, и их совместное распределение вероятностей дается теоремой Бапат-Бега .

С этого момента мы будем предполагать, что рассматриваемые случайные величины являются непрерывными, и, где это удобно, мы также будем предполагать, что они имеют функцию плотности вероятности (PDF), то есть они абсолютно непрерывны . В конце обсуждаются особенности анализа распределений, приписывающих массу точек (в частности, дискретных распределений ).

Кумулятивная функция распределения статистики заказов [ править ]

Для случайной выборки, как указано выше, с кумулятивным распределением , статистика порядка для этой выборки имеет кумулятивное распределение следующим образом ^[2] (где r указывает, какая статистика порядка):${\ Displaystyle F_ {X} (х)}$

${\displaystyle F_{X_{(r)}}(x)=\sum _{j=r}^{n}{\binom {n}{j}}[F_{X}(x)]^{j}[1-F_{X}(x)]^{n-j}}$

соответствующая функция плотности вероятности может быть получена из этого результата, и она оказывается

${\displaystyle f_{X_{(r)}}(x)={\frac {n!}{(r-1)!(n-r)!}}f_{X}(x)[F_{X}(x)]^{r-1}[1-F_{X}(x)]^{n-r}}$.

Более того, есть два особых случая, в которых легко вычислить функции CDF.

${\displaystyle F_{X_{(n)}}(x)={\text{Prob}}(\max\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=[F_{X}(x)]^{n}}$

${\displaystyle F_{X_{(1)}}(x)={\text{Prob}}(\min\{\,X_{1},\ldots ,X_{n}\,\}\leq x)=1-[1-F_{X}(x)]^{n}}$

Что может быть получено путем тщательного рассмотрения вероятностей.

Распределения вероятностей статистики заказов [ править ]

Статистические данные по заказам взяты из равномерного распределения [ править ]

В этом разделе мы покажем, что порядковая статистика равномерного распределения на единичном интервале имеет маргинальные распределения, принадлежащие семейству бета-распределения . Мы также даем простой метод получения совместного распределения любого количества порядковых статистик и, наконец, переводим эти результаты в произвольные непрерывные распределения с помощью cdf .

В этом разделе мы предполагаем, что это случайная выборка, полученная из непрерывного распределения с помощью cdf . Обозначая, мы получаем соответствующую случайную выборку из стандартного равномерного распределения . Обратите внимание, что статистика заказов тоже удовлетворяет .${\displaystyle X_{1},X_{2},\ldots ,X_{n}}$${\displaystyle F_{X}}$${\displaystyle U_{i}=F_{X}(X_{i})}$${\displaystyle U_{1},\ldots ,U_{n}}$${\displaystyle U_{(i)}=F_{X}(X_{(i)})}$

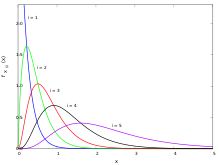
Функция плотности вероятности статистики порядка равна ^[3]${\displaystyle U_{(k)}}$

${\displaystyle f_{U_{(k)}}(u)={n! \over (k-1)!(n-k)!}u^{k-1}(1-u)^{n-k}}$

то есть статистика k- го порядка равномерного распределения является случайной величиной с бета-распределением . ^{[3] [4]}

${\displaystyle U_{(k)}\sim \operatorname {Beta} (k,n+1\mathbf {-} k).}$

Доказательство этих утверждений следующее. Чтобы быть между u и u  +  du , необходимо, чтобы ровно k  - 1 элементов выборки были меньше u , и чтобы хотя бы один был между u и u  + d u . Вероятность того, что в последнем интервале находится более одного, уже есть , поэтому мы должны вычислить вероятность того, что ровно k  - 1, 1 и n  -  k наблюдений попадают в интервалы , и соответственно. Это равно ( подробности см. В мультиномиальном распределении )${\displaystyle U_{(k)}}$${\displaystyle O(du^{2})}$${\displaystyle (0,u)}$${\displaystyle (u,u+du)}$${\displaystyle (u+du,1)}$

${\displaystyle {n! \over (k-1)!(n-k)!}u^{k-1}\cdot du\cdot (1-u-du)^{n-k}}$

и результат следует.

Среднее значение этого распределения равно k / ( n + 1).

Совместное распределение порядковой статистики равномерного распределения [ править ]

Точно так же для i  <  j можно показать , что совместная функция плотности вероятности статистик двух порядков U _{( i )}  <  U _{( j )} равна

${\displaystyle f_{U_{(i)},U_{(j)}}(u,v)=n!{u^{i-1} \over (i-1)!}{(v-u)^{j-i-1} \over (j-i-1)!}{(1-v)^{n-j} \over (n-j)!}}$

что ( с точностью до членов более высокого порядка , чем ) вероятность того, что я  - 1, 1, J  - 1 -  я , 1 и п  -  J выборки элементов падают в интервалах , , , , соответственно.${\displaystyle O(du\,dv)}$${\displaystyle (0,u)}$${\displaystyle (u,u+du)}$${\displaystyle (u+du,v)}$${\displaystyle (v,v+dv)}$${\displaystyle (v+dv,1)}$

Совершенно аналогичным образом рассуждают о выводе совместных распределений более высокого порядка. Удивительно, но совместная плотность статистики n-го порядка оказывается постоянной :

${\displaystyle f_{U_{(1)},U_{(2)},\ldots ,U_{(n)}}(u_{1},u_{2},\ldots ,u_{n})=n!.}$

Один из способов понять это - то, что неупорядоченный образец действительно имеет постоянную плотность, равную 1, и что их n ! разные перестановки выборки, соответствующие одной и той же последовательности порядковых статистик. Это связано с тем, что 1 / n ! объем области .${\displaystyle 0<u_{1}<\cdots <u_{n}<1}$

Используя приведенные выше формулы, можно вывести распределение диапазона статистик порядка, то есть распределение , то есть максимум минус минимум. В более общем плане , для , также имеет бета - распределение:${\displaystyle U_{(n)}-U_{(1)}}$${\displaystyle n\geq k>j\geq 1}$${\displaystyle U_{(k)}-U_{(j)}}$

Из этих формул мы можем вывести ковариацию между статистиками двух порядков:Формула следует из того, что и сравнивая это с где , что является фактическим распределением разницы.${\displaystyle U\sim Beta(k-j,n-(k-j)+1)}$

Статистика заказов, полученная из экспоненциального распределения [ править ]

Для случайных выборок из экспоненциального распределения с параметром λ каждая статистика порядка X _(i) для i = 1,2,3, ..., n имеет распределение${\displaystyle X_{1},X_{2},..,X_{n}}$

${\displaystyle X_{(i)}{\stackrel {d}{=}}{\frac {1}{\lambda }}\left(\sum _{j=1}^{i}{\frac {Z_{j}}{n-j+1}}\right)}$

где Z _j - стандартные экспоненциальные случайные величины iid (т.е. с параметром скорости 1). Этот результат был впервые опубликован Альфредом Реньи. ^{[5] [6]}

Статистика заказов, взятая из распределения Erlang [ править ]

Преобразование Лапласа статистики порядка может быть выбрано из распределения Эрланга с помощью метода подсчета путей ^{[ требуется пояснение ]} . ^[7]

Совместное распределение порядковой статистики абсолютно непрерывного распределения [ править ]

Если F _X является абсолютно непрерывной , она имеет плотность такая , что , и мы можем использовать подстановки${\displaystyle dF_{X}(x)=f_{X}(x)\,dx}$

${\displaystyle u=F_{X}(x)}$

и

${\displaystyle du=f_{X}(x)\,dx}$

чтобы получить следующие функции плотности вероятности для статистики порядка выборки размера n, взятой из распределения X :

${\displaystyle f_{X_{(k)}}(x)={\frac {n!}{(k-1)!(n-k)!}}[F_{X}(x)]^{k-1}[1-F_{X}(x)]^{n-k}f_{X}(x)}$

${\displaystyle f_{X_{(j)},X_{(k)}}(x,y)={\frac {n!}{(j-1)!(k-j-1)!(n-k)!}}[F_{X}(x)]^{j-1}[F_{X}(y)-F_{X}(x)]^{k-1-j}[1-F_{X}(y)]^{n-k}f_{X}(x)f_{X}(y)}$ куда ${\displaystyle x\leq y}$

${\displaystyle f_{X_{(1)},\ldots ,X_{(n)}}(x_{1},\ldots ,x_{n})=n!f_{X}(x_{1})\cdots f_{X}(x_{n})}$ куда ${\displaystyle x_{1}\leq x_{2}\leq \dots \leq x_{n}.}$

Применение: доверительные интервалы для квантилей [ править ]

Интересный вопрос заключается в том, насколько хорошо статистические данные о порядке служат для оценки квантилей основного распределения.

Пример небольшого размера выборки [ править ]

Самый простой случай, который следует рассмотреть, - насколько хорошо медиана выборки оценивает медианную совокупность.

В качестве примера рассмотрим случайную выборку размера 6. В этом случае медиана выборки обычно определяется как средняя точка интервала, ограниченного статистикой 3-го и 4-го порядка. Однако из предыдущего обсуждения мы знаем, что вероятность того, что этот интервал действительно содержит медианную популяцию, равна

${\displaystyle {6 \choose 3}(1/2)^{6}={5 \over 16}\approx 31\%.}$

Хотя медиана выборки, вероятно, является одной из лучших точечных оценок медианы совокупности, не зависящей от распределения , этот пример показывает, что она не особенно хороша в абсолютном выражении. В этом конкретном случае лучшим доверительным интервалом для медианы является интервал, ограниченный статистикой 2-го и 5-го порядка, который содержит медианное значение совокупности с вероятностью

${\displaystyle \left[{6 \choose 2}+{6 \choose 3}+{6 \choose 4}\right](1/2)^{6}={25 \over 32}\approx 78\%.}$

При таком небольшом размере выборки, если кто-то хочет иметь по крайней мере 95% уверенности, можно сказать, что медиана находится между минимумом и максимумом из 6 наблюдений с вероятностью 31/32 или приблизительно 97%. Фактически, размер 6 является наименьшим размером выборки, так что интервал, определяемый минимумом и максимумом, составляет по крайней мере 95% доверительный интервал для медианы совокупности.

Большой размер выборки [ править ]

Для равномерного распределения, поскольку п стремится к бесконечности, то р - ^й пробы квантиль асимптотически нормально распределены , так как она аппроксимируется

${\displaystyle U_{(\lceil np\rceil )}\sim AN\left(p,{\frac {p(1-p)}{n}}\right).}$

Для общего распределения F с непрерывной ненулевой плотностью в F  ⁻¹ ( p ) применяется аналогичная асимптотическая нормальность:

${\displaystyle X_{(\lceil np\rceil )}\sim AN\left(F^{-1}(p),{\frac {p(1-p)}{n[f(F^{-1}(p))]^{2}}}\right)}$

где F является функцией плотности и F  ^-1 является функцией квантиля , связанная с F . Одним из первых, кто упомянул и доказал этот результат, был Фредерик Мостеллер в его основополагающей статье 1946 года. ^[8] Дальнейшие исследования привели в 1960-х годах к представлению Бахадура, которое предоставляет информацию о границах ошибок.

Интересное наблюдение можно сделать в случае, когда распределение является симметричным, а медиана совокупности равна среднему значению совокупности. В этом случае выборочное среднее согласно центральной предельной теореме также асимптотически нормально распределено, но с дисперсией σ ² / n . Этот асимптотический анализ предполагает, что среднее значение превосходит медиану в случаях низкого эксцесса , и наоборот. Например, медиана дает лучшие доверительные интервалы для распределения Лапласа , в то время как среднее работает лучше для X , которые распределены нормально.

Доказательство [ править ]

Можно показать, что

${\displaystyle B(k,n+1-k)\ {\stackrel {\mathrm {d} }{=}}\ {\frac {X}{X+Y}},}$

куда

${\displaystyle X=\sum _{i=1}^{k}Z_{i},\quad Y=\sum _{i=k+1}^{n+1}Z_{i},}$

где Z _i являются независимыми одинаково распределенными экспоненциальными случайными величинами со скоростью 1. Так как X / n и Y / n асимптотически нормально распределены CLT, наши результаты основаны на применении дельта-метода .

Применение: непараметрическая оценка плотности [ править ]

Моменты распределения для статистики первого порядка можно использовать для разработки непараметрической оценки плотности. ^[9] Предположим, мы хотим оценить плотность в точке . Рассмотрим случайные величины , которым присвоена функция распределения . В частности, .${\displaystyle f_{X}}$${\displaystyle x^{*}}$${\displaystyle Y_{i}=|X_{i}-x^{*}|}$${\displaystyle g_{Y}(y)=f_{X}(y+x^{*})+f_{X}(x^{*}-y)}$${\displaystyle f_{X}(x^{*})={\frac {g_{Y}(0)}{2}}}$

Ожидаемое значение статистики первого порядка с учетом общего количества выборок,${\displaystyle Y_{(1)}}$${\displaystyle N}$

${\displaystyle E(Y_{(1)})={\frac {1}{(N+1)g(0)}}+{\frac {1}{(N+1)(N+2)}}\int _{0}^{1}Q''(z)\delta _{N+1}(z)\,dz}$

где - функция квантиля, связанная с распределением , и . Это уравнение в сочетании с методом складывания ножей становится основой для следующего алгоритма оценки плотности:${\displaystyle Q}$${\displaystyle g_{Y}}$${\displaystyle \delta _{N}(z)=(N+1)(1-z)^{N}}$

 Сырьё: образцы. точки оценки плотности. Параметр настройки (обычно 1/3).${\displaystyle N}$${\displaystyle \{x_{l}\}_{l=1}^{M}}$${\displaystyle a\in (0,1)}$ Выход: расчетная плотность в точках оценки.${\displaystyle \{{\hat {f}}_{l}\}_{l=1}^{M}}$

 1: Набор 2: Набор 3: Создать матрицу, содержащую подмножества с выборками в каждом.${\displaystyle m_{N}=round(N^{1-a})}$${\displaystyle s_{N}={\frac {N}{m_{N}}}}$${\displaystyle s_{N}\times m_{N}}$${\displaystyle M_{ij}}$${\displaystyle m_{N}}$${\displaystyle s_{N}}$ 4: Создайте вектор, чтобы удерживать оценки плотности.${\displaystyle {\hat {f}}}$ 5: для  do 6: для do 7: найти ближайшее расстояние до текущей точки в th подмножестве${\displaystyle l=1\to M}$  ${\displaystyle k=1\to m_{N}}$ ${\displaystyle d_{lk}}$${\displaystyle x_{l}}$${\displaystyle k}$ 8: конец для 9: вычислить среднее подмножество расстояний до 10: вычислить оценку плотности в 11: конец для 12: возврат${\displaystyle x_{l}:d_{l}=\sum _{k=1}^{m_{N}}{\frac {d_{lk}}{m_{N}}}}$${\displaystyle x_{l}:{\hat {f}}_{l}={\frac {1}{2(1+s_{N})d_{l}}}}$ ${\displaystyle {\hat {f}}}$

В отличие от параметров настройки на основе полосы пропускания / длины для подходов на основе гистограммы и ядра , параметром настройки для оценки плотности на основе статистики порядка является размер подмножеств выборки. Такая оценка более надежна, чем подходы на основе гистограммы и ядра, например плотности, подобные распределению Коши (в котором отсутствуют конечные моменты), могут быть выведены без необходимости специальных модификаций, таких как полоса пропускания на основе IQR . Это потому, что первый момент статистики заказа всегда существует, если ожидаемое значение базового распределения существует, но обратное не обязательно верно. ^[10]

Работа с дискретными переменными [ править ]

Предположит , являются IID случайных величин из дискретного распределения с функцией распределения и функцией вероятности массовой . Чтобы найти вероятности статистики порядка, сначала нужны три значения, а именно${\displaystyle X_{1},X_{2},...,X_{n}}$${\displaystyle F(x)}$ ${\displaystyle f(x)}$${\displaystyle k^{\text{th}}}$

${\displaystyle p_{1}=P(X<x)=F(x)-f(x),\ p_{2}=P(X=x)=f(x),{\text{ and }}p_{3}=P(X>x)=1-F(x).}$

Кумулятивную функцию распределения статистики заказов можно вычислить, отметив, что${\displaystyle k^{\text{th}}}$

${\displaystyle {\begin{aligned}P(X_{(k)}\leq x)&=P({\text{there are at least }}k{\text{ observations less than or equal to }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}p_{3}^{j}(p_{1}+p_{2})^{n-j}.\end{aligned}}}$

Точно так же дается${\displaystyle P(X_{(k)}<x)}$

${\displaystyle {\begin{aligned}P(X_{(k)}<x)&=P({\text{there are at least }}k{\text{ observations less than }}x),\\&=P({\text{there are at most }}n-k{\text{ observations greater than or equal to }}x),\\&=\sum _{j=0}^{n-k}{n \choose j}(p_{2}+p_{3})^{j}(p_{1})^{n-j}.\end{aligned}}}$

Обратите внимание, что функция массы вероятности - это просто разность этих значений, то есть${\displaystyle X_{k}}$

${\displaystyle {\begin{aligned}P(X_{(k)}=x)&=P(X_{(k)}\leq x)-P(X_{(k)}<x),\\&=\sum _{j=0}^{n-k}{n \choose j}\left(p_{3}^{j}(p_{1}+p_{2})^{n-j}-(p_{2}+p_{3})^{j}(p_{1})^{n-j}\right),\\&=\sum _{j=0}^{n-k}{n \choose j}\left((1-F(x))^{j}(F(x))^{n-j}-(1-F(x)+f(x))^{j}(F(x)-f(x))^{n-j}\right).\end{aligned}}}$

Вычисление статистики заказов [ править ]

Задача вычисления k- го наименьшего (или наибольшего) элемента списка называется проблемой выбора и решается с помощью алгоритма выбора. Хотя эта проблема сложна для очень больших списков, были созданы сложные алгоритмы выбора, которые могут решить эту проблему во времени, пропорциональном количеству элементов в списке, даже если список полностью неупорядочен. Если данные хранятся в определенных специализированных структурах данных, это время можно уменьшить до O (log n ). Во многих приложениях требуется вся статистика заказов, и в этом случае можно использовать алгоритм сортировки, а затраченное время равно O ( n log n ).

См. Также [ править ]

• Rankit
• Коробчатый сюжет
• Сопутствующие (статистика)
• Распределение Фишера – Типпета
• Теорема Бапата – Бега для статистики порядка независимых, но не обязательно одинаково распределенных случайных величин
• Полином Бернштейна
• L-оценка - линейные комбинации статистик заказов
• Распределение по рангам
• Алгоритм выбора

Примеры статистики заказов [ править ]

• Максимум и минимум выборки
• Квантиль
• Процентиль
• Дециль
• Квартиль
• Медиана

Эта статья включает в себя список общих ссылок , но он остается в значительной степени непроверенным, поскольку в нем отсутствует достаточное количество соответствующих встроенных ссылок . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Декабрь 2010 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

Ссылки [ править ]

Внешние ссылки [ править ]

• Статистика заказа на PlanetMath . Проверено 02 февраля 2005 г.
• Вайсштейн, Эрик В. «Статистика порядка» . MathWorld . Проверено 02 февраля 2005 г.
• Статистика динамического заказа исходного кода C ++