Коробчатый сюжет

Рис. 1. Ящичковая диаграмма данных эксперимента Майкельсона – Морли.

В описательных статистиках , коробка участок или boxplot является способом графический изображающими групп числовых данных через их квартиль . Box участки также могут иметь линии , простирающиеся от коробки ( усов ) , указывающей изменчивости за пределами верхней и нижней квартили, следовательно , термины коробчатых и усы-сюжет и коробчатой и усы-схему . Выбросы могут быть нанесены на график как отдельные точки. Ящичные диаграммы не являются параметрическими : они отображают вариации в выборках статистической совокупности без каких-либо предположений относительно основного статистического распределения.(хотя коробчатая диаграмма Тьюки предполагает симметрию усов и нормальность их длины). Расстояние между различными частями прямоугольника указывает на степень дисперсии (разброса) и асимметрии данных и показывает выбросы . В дополнение к самим точкам они позволяют визуально оценить различные L-оценки , в частности межквартильный размах , середину , размах , средний диапазон и трисредний . Коробчатые диаграммы можно рисовать как по горизонтали, так и по вертикали. Коробчатые диаграммы получили свое название от прямоугольника посередине.

История коробчатого сюжета [ править ]

Полоса дальности была представлена Мэри Элеонор Спир в 1952 году ^[1] и снова в 1969 году. ^[2] График ящика и усов был впервые представлен в 1970 году Джоном Тьюки , который позже опубликовал на эту тему в 1977 году ^[3].

Элементы коробчатой графики [ править ]

Рис. 2. Коробчатая диаграмма с усами от минимума до максимума.

Рис. 3. Та же коробчатая диаграмма с усами с максимальным IQR 1,5.

Коробчатая диаграмма - это стандартизированный способ отображения набора данных на основе пятизначной сводки : минимум, максимум, медиана выборки, а также первый и третий квартили.

Минимум ( Q ₀ или 0-й процентиль) : самая низкая точка данных без каких-либо выбросов.

Максимум ( Q ₄ или 100-й процентиль) : наибольшая точка данных без каких-либо выбросов.

Медиана ( Q ₂ или 50-й процентиль) : среднее значение набора данных.

Первый квартиль ( Q ₁ или 25-й процентиль) : также известный как нижний квартиль q _n (0,25), это медиана нижней половины набора данных.

Третий квартиль ( Q ₃ или 75-й процентиль) : также известный как верхний квартиль q _n (0,75), является медианным значением верхней половины набора данных. ^[4]

Важным элементом, используемым для построения прямоугольной диаграммы путем определения минимальных и максимальных значений данных, которые возможны, но не являются частью вышеупомянутой пятизначной сводки, является межквартильный диапазон или IQR, обозначенный ниже:

Межквартильный размах (IQR) : это расстояние между верхним и нижним квартилями.

{\ displaystyle {\ text {IQR}} = Q_ {3} -Q_ {1} = q_ {n} (0,75) -q_ {n} (0,25)}

Коробчатая диаграмма состоит из двух частей, прямоугольника и набора усов, показанных на рисунке 2. Самая низкая точка - это минимум набора данных, а самая высокая точка - максимум набора данных. Прямоугольник проведен от Q ₁ до Q ₃ с горизонтальной линией посередине для обозначения медианы.

Тот же набор данных также может быть представлен в виде прямоугольной диаграммы, показанной на рисунке 3. Сверху верхнего квартиля измеряется расстояние, в 1,5 раза превышающее IQR, и проводится усы до самой большой наблюдаемой точки из набора данных, которая попадает в этот расстояние. Точно так же расстояние, в 1,5 раза превышающее IQR, измеряется ниже нижнего квартиля, а усы протягиваются до нижней наблюдаемой точки из набора данных, которая попадает в это расстояние. Все остальные наблюдаемые точки отображаются как выбросы. ^[5]

Однако усы могут представлять несколько возможных альтернативных значений, среди которых:

минимум и максимум всех данных (как на рисунке 2)
одно стандартное отклонение выше и ниже среднего значения данных
9-й процентиль и 91-й процентиль
2-й процентиль и 98-й процентиль .

Любые данные, не включенные между усами, должны быть нанесены как выброс с точкой, маленьким кружком или звездочкой, но иногда этого не делается.

Некоторые коробчатые диаграммы включают дополнительный символ для представления среднего значения данных. ^[6]^[7]

На некоторых коробчатых диаграммах на каждом усе перед концом наносится перекрестие.

Редко коробчатые диаграммы могут быть представлены вообще без усов.

Из-за этой изменчивости уместно описать соглашение, используемое для усов и выбросов, в подписи к графику.

Необычные процентили 2%, 9%, 91%, 98% иногда используются для штриховки усов и концов усов, чтобы показать семизначную сводку . Если данные распределены нормально , места семи отметок на прямоугольной диаграмме будут равномерно распределены.

Варианты [ править ]

Рис. 4. Диаграммы с четырьмя коробками, с надрезами и без них и переменной шириной

С тех пор, как математик Джон У. Тьюки популяризировал этот тип отображения визуальных данных в 1969 году, было описано несколько вариантов традиционной прямоугольной диаграммы. Двумя наиболее распространенными являются прямоугольные диаграммы переменной ширины и прямоугольные диаграммы с надрезом (см. Рисунок 4).

Графики ящиков переменной ширины иллюстрируют размер каждой группы, данные которой выводятся на график, делая ширину ящика пропорциональной размеру группы. Популярное соглашение - сделать ширину прямоугольника пропорциональной квадратному корню из размера группы. ^[8]

На прямоугольных диаграммах с надрезом применяется «надрез» или сужение прямоугольника вокруг медианы. Вырезы полезны, поскольку предлагают приблизительное представление о значении разницы медиан; если выемки двух прямоугольников не перекрываются, это свидетельствует о статистически значимой разнице между медианами. ^[8] Ширина меток пропорциональна межквартильному диапазону (IQR) выборки и обратно пропорциональна квадратному корню из размера выборки. Однако существует неопределенность относительно наиболее подходящего множителя (поскольку он может варьироваться в зависимости от схожести дисперсий выборок). ^[8] Одно из соглашений - использовать . ^[9] ${\ displaystyle \ pm {\ frac {1.58 {\ text {IQR}}} {\ sqrt {n}}}}$

Скорректированные ящичные диаграммы предназначены для неравномерного распределения . Они полагаются на статистику асимметрии для пары . ^[10] Для среднего значения MC длины верхних и нижних усов соответственно определены как

{\ displaystyle {\ begin {matrix} 1.5 {\ text {IQR}} \ cdot e ^ {3 {\ text {MC}}}, & 1.5 {\ text {IQR}} \ cdot e ^ {- 4 { \ text {MC}}} {\ text {if}} {\ text {MC}} \ geq 0, \\ 1.5 {\ text {IQR}} \ cdot e ^ {4 {\ text {MC}}}, & 1.5 {\ text {IQR}} \ cdot e ^ {- 3 {\ text {MC}}} {\ text {if}} {\ text {MC}} \ leq 0. \ end {matrix}}}

Для симметричных распределений медпара будет равна нулю, и это сводится к диаграмме Тьюки с равными длинами усов для обоих усов. $1.5{\text{ IQR}}$

Другие виды графиков, такие как графики скрипки и бобовые графики, могут показать разницу между одномодальным и мультимодальным распределениями, разницу, которую нельзя увидеть с исходной коробчатой графикой. ^[11]

Примеры [ править ]

Пример без выбросов [ править ]

Рисунок 5. Сгенерированный рисунок прямоугольной диаграммы нашего примера слева без выбросов.

В течение дня в течение дня измерялись почасовые измерения температуры в градусах Фаренгейта. Записанные значения перечислены в следующем порядке: 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.

Ящичковая диаграмма данных может быть создана путем вычисления пяти соответствующих значений: минимума, максимума, медианы, первого квартиля и третьего квартиля.

Минимум - это наименьший номер набора. В этом случае минимальная дневная температура составляет 57 ° F.

Максимум - это наибольшее количество набора. В этом случае максимальная дневная температура составляет 81 ° F.

Медиана - это «средний» номер упорядоченного набора. Это означает, что ровно 50% элементов меньше медианы и 50% элементов больше медианы. Медиана этого заказанного набора составляет 70 ° F.

Значение первого квартиля - это число, обозначающее одну четверть упорядоченного набора. Другими словами, ровно 25% элементов меньше первого квартиля и ровно 75% элементов больше. Значение первого квартиля можно легко определить, найдя «среднее» число между минимумом и медианой. Для почасовой температуры «среднее» число между 57 ° F и 70 ° F составляет 66 ° F.

Значение третьего квартиля - это число, обозначающее три четверти упорядоченного набора. Другими словами, ровно 75% элементов меньше первого квартиля и 25% элементов больше. Значение третьего квартиля можно легко определить, найдя «среднее» число между медианой и максимумом. Для почасовой температуры «среднее» число между 70 ° F и 81 ° F составляет 75 ° F.

Межквартильный размах, или IQR, можно рассчитать:

{\text{IQR}}=Q_{3}-Q_{1}=75^{\circ }F-66^{\circ }F=9^{\circ }F.

Следовательно, $1.5{\text{IQR}}=1.5\cdot 9^{\circ }F=13.5^{\circ }F.$

1.5 IQR выше третьего квартиля:

Q3+1.5{\text{ IQR}}=75^{\circ }F+13.5^{\circ }F=88.5^{\circ }F.

1.5IQR ниже первого квартиля:

Q_{1}-1.5{\text{ IQR}}=66^{\circ }F-13.5^{\circ }F=52.5^{\circ }F.

Верхний ус на прямоугольной диаграмме - это самый большой номер набора данных, меньший, чем 1,5IQR выше третьего квартиля. Здесь 1,5IQR выше третьего квартиля составляет 88,5 ° F, а максимальное - 81 ° F. Следовательно, верхний ус нарисован на максимальном значении 81 ° F.

Точно так же нижний ус на прямоугольной диаграмме - это наименьший номер набора данных, превышающий 1,5IQR ниже первого квартиля. Здесь 1,5IQR ниже первого квартиля составляет 52,5 ° F, а минимальное - 57 ° F. Поэтому нижний ус нарисован на минимальном значении 57 ° F.

Пример с выбросами [ править ]

Рисунок 6. Сгенерированная коробчатая диаграмма нашего примера слева с выбросами.

Выше приведен пример без выбросов. Вот дополнительный пример с выбросами:

Заказанный набор: 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79 , 89.

В этом примере изменяются только первый и последний номер. Медиана, третий квартиль и первый квартиль остаются прежними.

В этом случае максимальное значение составляет 89 ° F, а на 1,5IQR выше третьего квартиля - 88,5 ° F. Максимальное значение превышает 1,5IQR плюс третий квартиль, поэтому максимальное значение является выбросом. Следовательно, верхние усы нарисованы с максимальным значением, меньшим, чем 1,5IQR, над третьим квартилем, который составляет 79 ° F.

Точно так же минимум составляет 52 ° F, а IQR на 1,5 ниже первого квартиля составляет 52,5 ° F. Минимум меньше 1,5IQR минус первый квартиль, поэтому минимум также является выбросом. Следовательно, нижние усы отображаются при наименьшем значении, превышающем 1,5IQR, ниже первого квартиля, который составляет 57 ° F.

В случае больших наборов данных [ править ]

Общее уравнение для вычисления эмпирических квантилей [ править ]

q_{n}(p)=x_{(k)}+\alpha (x_{(k+1)}-x_{(k)})

{\text{with }}k=[p(n+1)]{\text{ and }}\alpha =p(n+1)-k

Используя приведенный выше пример с 24 точками данных, что означает n = 24, можно также вычислить медианное значение, первый и третий квартили математически и визуально.

Медиана : $q_{n}(0.5)=q_{(12)}+(0.5\cdot 25-12)\cdot (x_{(13)}-x_{(12)})=70+(0.5\cdot 25-12)\cdot (70-70)=70$

Первый квартиль : $q_{n}(0.25)=q_{(6)}+(0.25\cdot 25-6)\cdot (x_{(7)}-x_{(6)})=66+(0.25\cdot 25-6)\cdot (66-66)=66$

Третий квартиль : $q_{n}(0.75)=q_{(18)}+(0.75\cdot 25-18)\cdot (x_{(19)}-x_{(18)})=75+(0.75\cdot 25-18)\cdot (75-75)=75$

Визуализация [ править ]

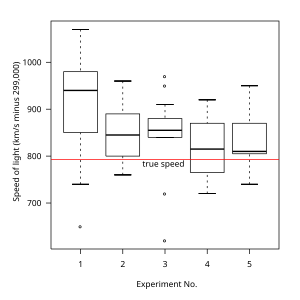
Рис. 7. Коробчатая диаграмма и функция плотности вероятности (pdf) для нормальной N (0,1σ ² ) совокупности

Ящичная диаграмма позволяет быстро графически исследовать один или несколько наборов данных. Ящичные диаграммы могут показаться более примитивными, чем гистограмма или оценка плотности ядра, но у них есть некоторые преимущества. Они занимают меньше места и поэтому особенно полезны для сравнения распределений между несколькими группами или наборами данных (см. Пример на рисунке 1). Выбор количества и ширины интервалов может сильно повлиять на внешний вид гистограммы, а выбор полосы пропускания может сильно повлиять на внешний вид оценки плотности ядра.

Поскольку рассмотрение статистического распределения является более обычным делом, чем просмотр прямоугольной диаграммы, сравнение прямоугольной диаграммы с функцией плотности вероятности (теоретическая гистограмма) для нормального распределения N (0, σ ² ) может быть полезным инструментом для понимания прямоугольной диаграммы. (Рисунок 7).

Рисунок 8. Коробчатые диаграммы, отображающие перекос

См. Также [ править ]

Двумерный коробчатый график
Свечной график
Исследовательский анализ данных
Веерная диаграмма
Пятизначное резюме
Функциональная коробчатая диаграмма
Семизначное резюме

Ссылки [ править ]

↑ Копье, Мэри Элеонора (1952). Графическая статистика . Макгроу Хилл. п. 166.
↑ Копье, Мэри Элеонора. (1969). Практические приемы построения графиков . Нью-Йорк: Макгроу-Хилл. ISBN 0070600104. OCLC 924909765 .
^ Уикхэм, Хэдли; Стрыевский, Лиза. «40 лет коробчатым сюжетам» (PDF) . Проверено 24 декабря 2020 года .
^ Холмс, Александр; Ильловски, Барбара; Дин, Сьюзан. «Вводная бизнес-статистика» . OpenStax .
^ Dekking, FM (2005). Современное введение в вероятность и статистику . Springer. стр. 234 -238. ISBN 1-85233-896-2.
^ Фригге, Майкл; Хоглин, Дэвид С .; Иглевич, Борис (февраль 1989 г.). «Некоторые реализации коробчатого графика». Американский статистик . 43 (1): 50–54. DOI : 10.2307 / 2685173 . JSTOR 2685173 .
^ Мармолехо-Рамос, Ф .; Тиан, С. (2010). «Коробчатая диаграмма смещения. Коробчатая диаграмма, основанная на важной сводной статистике вокруг среднего» . Международный журнал психологических исследований . 3 (1): 37–46. DOI : 10.21500 / 20112084.823 .
^ a b c Макгилл, Роберт; Тьюки, Джон В .; Ларсен, Уэйн А. (февраль 1978 г.). «Вариации коробчатых сюжетов». Американский статистик . 32 (1): 12–16. DOI : 10.2307 / 2683468 . JSTOR 2683468 .
^ «R: Статистика коробчатой диаграммы» . R руководство . Проверено 26 июня 2011 года .
^ Хьюберт, М .; Вандервирен, Э. (2008). «Скорректированный коробчатый график для искаженного распределения». Вычислительная статистика и анализ данных . 52 (12): 5186–5201. CiteSeerX 10.1.1.90.9812 . DOI : 10.1016 / j.csda.2007.11.008 .
^ Уикхэм, Хэдли; Стрыевский, Лиза (2011). «40 лет коробчатым сюжетам» (PDF) .

Дальнейшее чтение [ править ]

Джон У. Тьюки (1977). Исследовательский анализ данных . Эддисон-Уэсли .
Бенджамини, Ю. (1988). «Открывая коробку коробчатого сюжета». Американский статистик . 42 (4): 257–262. DOI : 10.2307 / 2685133 . JSTOR 2685133 .
Rousseeuw, PJ ; Ruts, I .; Тьюки, JW (1999). "Багажник: двумерный коробчатый сюжет". Американский статистик . 53 (4): 382–387. DOI : 10.2307 / 2686061 . JSTOR 2686061 .

Внешние ссылки [ править ]

Викискладе есть медиафайлы по теме коробчатых сюжетов .

Он-лайн калькулятор коробчатых графиков с пояснениями и примерами (есть пример beeswarm)
Beeswarm Boxplot - наложение полосовой диаграммы с колебаниями частоты поверх коробчатой диаграммы
Сложный онлайн-конструктор коробчатых диаграмм с примерами данных - см. Также BoxPlotR: веб-инструмент для создания коробчатых диаграмм Spitzer et al. Nature Methods 11, 121–122 (2014).

[1] Копье, Мэри Элеонора (1952). Графическая статистика . Макгроу Хилл. п. 166.

[2] Копье, Мэри Элеонора. (1969). Практические приемы построения графиков . Нью-Йорк: Макгроу-Хилл. ISBN 0070600104. OCLC 924909765 .

[3] Уикхэм, Хэдли; Стрыевский, Лиза. «40 лет коробчатым сюжетам» (PDF) . Проверено 24 декабря 2020 года .

[4] Холмс, Александр; Ильловски, Барбара; Дин, Сьюзан. «Вводная бизнес-статистика» . OpenStax .

[5] Dekking, FM (2005). Современное введение в вероятность и статистику . Springer. стр. 234 -238. ISBN 1-85233-896-2.

[frigge_hoaglin_iglewicz2-6] Фригге, Майкл; Хоглин, Дэвид С .; Иглевич, Борис (февраль 1989 г.). «Некоторые реализации коробчатого графика». Американский статистик . 43 (1): 50–54. DOI : 10.2307 / 2685173 . JSTOR 2685173 .

[7] Мармолехо-Рамос, Ф .; Тиан, С. (2010). «Коробчатая диаграмма смещения. Коробчатая диаграмма, основанная на важной сводной статистике вокруг среднего» . Международный журнал психологических исследований . 3 (1): 37–46. DOI : 10.21500 / 20112084.823 .

[mcgill_tukey_larsen-8] Макгилл, Роберт; Тьюки, Джон В .; Ларсен, Уэйн А. (февраль 1978 г.). «Вариации коробчатых сюжетов». Американский статистик . 32 (1): 12–16. DOI : 10.2307 / 2683468 . JSTOR 2683468 .

[Rboxplotstats-9] «R: Статистика коробчатой диаграммы» . R руководство . Проверено 26 июня 2011 года .

[Hubert2008-10] Хьюберт, М .; Вандервирен, Э. (2008). «Скорректированный коробчатый график для искаженного распределения». Вычислительная статистика и анализ данных . 52 (12): 5186–5201. CiteSeerX 10.1.1.90.9812 . DOI : 10.1016 / j.csda.2007.11.008 .

[11] Уикхэм, Хэдли; Стрыевский, Лиза (2011). «40 лет коробчатым сюжетам» (PDF) .

[1]