Геометрия расстояния

Геометрия расстояния - это характеристика и исследование наборов точек, основанное только на заданных значениях расстояний между парами элементов. ^{[1] [2] [3]} Говоря более абстрактно, это изучение полуметрических пространств и изометрических преобразований между ними. С этой точки зрения его можно рассматривать как предмет общей топологии . ^[4]

Исторически первым результатом дистанционной геометрии является формула Герона в I веке нашей эры. Современная теория началась в 19 веке с работ Артура Кейли , за которой последовали более обширные разработки в 20 веке Карлом Менгером и другими.

Проблемы возникают Расстояние геометрии всякий раз , когда нужно , чтобы вывести форму конфигурации точек ( относительные позиции ) от расстояния между ними, например, в биологии , ^[4] Датчик сети , ^[5] геодезические , навигации , картографии и физике .

Введение и определения [ править ]

Понятия дистанционной геометрии сначала будут объяснены путем описания двух конкретных проблем.

Проблема гиперболической навигации

Первая проблема: гиперболическая навигация [ править ]

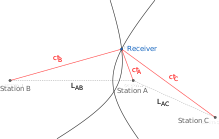
Рассмотрим три наземные радиостанции A, B, C, местоположение которых известно. Радиоприемник находится в неизвестном месте. Время, необходимое для прохождения радиосигнала от станций до приемника, неизвестно, но известны разницы во времени и . По ним можно узнать разницу расстояний и , по которому можно определить положение приемника.${\displaystyle {\displaystyle t_{A},t_{B},t_{C}}}$${\displaystyle {\displaystyle t_{A}-t_{B}}}$${\displaystyle {\displaystyle t_{A}-t_{C}}}$${\displaystyle c({\displaystyle t_{A}-t_{B}})}$${\displaystyle c({\displaystyle t_{A}-t_{C}})}$

Вторая проблема: уменьшение размеров [ править ]

При анализе данных часто дается список данных, представленных в виде векторов , и нужно выяснить, лежат ли они в аффинном подпространстве низкой размерности. Низкоразмерное представление данных имеет множество преимуществ, таких как экономия места для хранения, времени вычислений и лучшего понимания данных.${\displaystyle \mathbf {v} =(x_{1},\cdots ,x_{n})\in \mathbb {R} ^{n}}$

Определения [ править ]

Теперь мы формализуем некоторые определения, которые естественным образом возникают при рассмотрении наших задач.

Полиметрический пробел [ править ]

Учитывая список точек , мы можем произвольно определять расстояние между парами точек списка , . Это определяет полуметрическое пространство : метрическое пространство без неравенства треугольника .${\displaystyle R=\{P_{0},\cdots ,P_{n}\}}$${\displaystyle n\geq 0}$${\displaystyle d_{ij}>0}$${\displaystyle 0\leq i<j\leq n}$

Явный, мы определяем полуметрическое пространство как совокупность непустого снабженный полуметрика таким образом , что для всех ,${\displaystyle R}$${\displaystyle d:R\times R\to [0,\infty )}$${\displaystyle x,y\in R}$

1. Позитивность:   тогда и только тогда, когда   .${\displaystyle d(x,y)=0}$${\displaystyle x=y}$
2. Симметрия: .${\displaystyle d(x,y)=d(y,x)}$

Любое метрическое пространство заведомо полуметрическое. В частности, , то -мерное евклидово пространство , является каноническим метрическим пространством в дистанционной геометрии.${\displaystyle \mathbb {R} ^{k}}$${\displaystyle k}$

Неравенство треугольника опущено в определении, потому что мы не хотим налагать больше ограничений на расстояния, чем простое требование, чтобы они были положительными.${\displaystyle d_{ij}}$

На практике полуметрические пространства естественным образом возникают из-за неточных измерений. Например, при наличии трех точек на линии с , неточное измерение может дать , нарушая неравенство треугольника.${\displaystyle A,B,C}$${\displaystyle d_{AB}=1,d_{BC}=1,d_{AC}=2}$${\displaystyle d_{AB}=0.99,d_{BC}=0.98,d_{AC}=2.00}$

Изометрические вложения [ править ]

Учитывая два полуметрических пространства, , изометрическое вложение из к является карта , которая сохраняет полуметрика, то есть, для всех , .${\displaystyle (R,d),(R',d')}$${\displaystyle R}$${\displaystyle R'}$${\displaystyle f:R\to R'}$${\displaystyle x,y\in R}$${\displaystyle d(x,y)=d'(f(x),f(y))}$

Например, учитывая конечное полуметрическое пространство, определенное выше, изометрическое вложение в определяется точками , такими, что для всех .${\displaystyle (R,d)}$${\textstyle A_{0},A_{1},\ldots ,A_{n}\in {\displaystyle \mathbb {R} ^{k}}}$${\displaystyle d(A_{i},A_{j})=d_{ij}}$${\displaystyle 0\leq i<j\leq n}$

Аффинная независимость [ править ]

Принимая во внимание точки , они определяются как аффинно независимы , если и только если они не могут поместиться в одном мерном аффинном подпространстве , для любого , тогда и только тогда - симплекс они охватывают, имеет положительную -VOLUME, то есть .${\textstyle A_{0},A_{1},\ldots ,A_{n}\in {\displaystyle \mathbb {R} ^{k}}}$${\displaystyle l}$${\displaystyle \mathbb {R} ^{k}}$${\displaystyle l<n}$${\displaystyle n}$${\displaystyle v_{n}}$${\displaystyle n}$${\displaystyle Vol_{n}(v_{n})>0}$

В общем случае, когда они аффинно независимы, поскольку общий n-симплекс невырожден. Например, 3 точки на плоскости, как правило, не коллинеарны, потому что треугольник, который они охватывают, не вырождается в отрезок прямой. Точно так же 4 точки в пространстве, как правило, не компланарны, потому что тетраэдр, который они охватывают, не вырождается в плоский треугольник.${\displaystyle k\geq n}$

Когда , они должны быть аффинно зависимыми. Это можно увидеть, заметив, что любой -симплекс, который может поместиться внутри, должен быть «плоским».${\displaystyle n>k}$${\displaystyle n}$${\displaystyle \mathbb {R} ^{k}}$

Детерминанты Кэли-Менгера [ править ]

Определители Кэли – Менгера , названные в честь Артура Кэли и Карла Менгера, являются определителями матриц расстояний между наборами точек.

Пусть есть n  + 1 точка в полуметрическом пространстве, их определитель Кэли – Менгера определяется формулой${\textstyle A_{0},A_{1},\ldots ,A_{n}}$

${\displaystyle CM(A_{0},\cdots ,A_{n})={\begin{vmatrix}0&d_{01}^{2}&d_{02}^{2}&\cdots &d_{0n}^{2}&1\\d_{01}^{2}&0&d_{12}^{2}&\cdots &d_{1n}^{2}&1\\d_{02}^{2}&d_{12}^{2}&0&\cdots &d_{2n}^{2}&1\\\vdots &\vdots &\vdots &\ddots &\vdots &\vdots \\d_{0n}^{2}&d_{1n}^{2}&d_{2n}^{2}&\cdots &0&1\\1&1&1&\cdots &1&0\end{vmatrix}}}$

Если , то они составляют вершины (возможно, вырожденного ) n-симплекса в . Можно показать, что ^[6] n-мерный объем симплекса удовлетворяет${\textstyle A_{0},A_{1},\ldots ,A_{n}\in {\displaystyle \mathbb {R} ^{k}}}$${\displaystyle {\displaystyle v_{n}}}$${\displaystyle \mathbb {R} ^{k}}$${\displaystyle {\displaystyle v_{n}}}$

${\displaystyle Vol_{n}(v_{n})^{2}={\frac {(-1)^{n+1}}{(n!)^{2}2^{n}}}CM(A_{0},\cdots ,A_{n})}$.

Обратите внимание, что в случае , мы имеем , что означает, что «0-мерный объем» 0-симплекса равен 1, то есть в 0-симплексе есть 1 точка.${\displaystyle n=0}$${\displaystyle Vol_{0}(v_{0})=1}$

${\textstyle A_{0},A_{1},\ldots ,A_{n}}$аффинно независимы тогда и только тогда , когда . Таким образом, определители Кэли – Менгера предоставляют вычислительный способ доказательства аффинной независимости.${\displaystyle Vol_{n}(v_{n})>0}$${\displaystyle (-1)^{n+1}CM(A_{0},\cdots ,A_{n})>0}$

Если , то точки должны быть аффинно зависимыми, таким образом . В статье Кэли 1841 года изучается частный случай , то есть любые 5 точек в 3-мерном пространстве должны иметь .${\displaystyle k<n}$${\displaystyle CM(A_{0},\cdots ,A_{n})=0}$${\displaystyle k=3,n=4}$${\displaystyle A_{0},\cdots ,A_{4}}$${\displaystyle CM(A_{0},\cdots ,A_{4})=0}$

История [ править ]

Первым результатом дистанционной геометрии является формула Герона из I века нашей эры, которая дает площадь треугольника из расстояний между его тремя вершинами. Формула Брахмагупты из 7 века нашей эры обобщает ее на циклические четырехугольники . Тарталья из 16-го века нашей эры обобщил его, чтобы дать объем тетраэдра, исходя из расстояний между его четырьмя вершинами.

Современная теория дистанционной геометрии началась с Автора Кэли и Карла Менгера . ^[7] Кэли опубликовал определитель Кэли в 1841 г. ^[8], который является частным случаем общего определителя Кэли – Менгера. Менгер доказал в 1928 году характеристическую теорему для всех полуметрических пространств, изометрически вложимых в n- мерное евклидово пространство . ^{[9] [10]} В 1931 году Менгер использовал отношения расстояния, чтобы дать аксиоматическую трактовку евклидовой геометрии. ^[11]${\displaystyle \mathbb {R} ^{n}}$

В книге Леонарда Блюменталя ^[12] дается общий обзор дистанционной геометрии на уровне выпускников, большая часть которой впервые рассматривается на английском языке, когда она была опубликована.

Теорема Менгера о характеризации [ править ]

Менгер доказал следующую характеризационную теорему полуметрических пространств: ^[2]

Полиметрическое пространство изометрически вложимо в -мерное евклидово пространство , но не входит ни в какое , если и только если:${\displaystyle (R,d)}$${\displaystyle n}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathbb {R} ^{m}}$${\displaystyle 0\leq m<n}$

1. ${\displaystyle R}$содержит -точечное подмножество , изометрическое с аффинно независимым -точечным подмножеством ;${\displaystyle (n+1)}$${\displaystyle S}$${\displaystyle (n+1)}$${\displaystyle \mathbb {R} ^{n}}$
2. Любое подмножество точек, полученное добавлением любых двух дополнительных точек в , конгруэнтно подмножеству точек в .${\displaystyle (n+3)}$${\displaystyle S'}$${\displaystyle R}$${\displaystyle S}$${\displaystyle (n+3)}$${\displaystyle \mathbb {R} ^{n}}$

Доказательство этой теоремы в несколько ослабленном виде (для метрических пространств вместо полуметрических) содержится в ^[13].

Характеристика через детерминанты Кэли-Менгера [ править ]

В книге Блюметала доказаны следующие результаты. ^[12]

Встраивание точек в ${\displaystyle n+1}$${\displaystyle \mathbb {R} ^{n}}$[ править ]

Учитывая полуметрику пространства , с , а , , изометрическое вложение INTO определяется , таким образом, что для всех .${\displaystyle (S,d)}$${\displaystyle S=\{P_{0},\cdots ,P_{n}\}}$${\displaystyle d(P_{i},P_{j})=d_{ij}\geq 0}$${\displaystyle 0\leq i<j\leq n}$${\displaystyle (S,d)}$${\displaystyle \mathbb {R} ^{n}}$${\textstyle A_{0},A_{1},\ldots ,A_{n}\in {\displaystyle \mathbb {R} ^{n}}}$${\displaystyle d(A_{i},A_{j})=d_{ij}}$${\displaystyle 0\leq i<j\leq n}$

Снова возникает вопрос, существует ли такое изометрическое вложение для .${\displaystyle (S,d)}$

Необходимое условие легко увидеть: для всех , пусть будет к симплекс образован , то${\displaystyle k=1,\cdots ,n}$${\displaystyle v_{k}}$${\textstyle A_{0},A_{1},\ldots ,A_{k}}$

${\displaystyle (-1)^{k+1}CM(P_{0},\cdots ,P_{k})=(-1)^{k+1}CM(A_{0},\cdots ,A_{k})=2^{k}(k!)^{k}Vol_{k}(v_{k})^{2}\geq 0}$

Верно и обратное. То есть, если для всех ,${\displaystyle k=1,\cdots ,n}$

${\displaystyle (-1)^{k+1}CM(P_{0},\cdots ,P_{k})\geq 0}$,

тогда такое вложение существует.

Далее, такое вложение единственно с точностью до изометрии в . То есть, для любых двух изометрических вложений, определенных с помощью , и , существует (не обязательно уникальная) изометрия , такая что для всех . Они уникальны тогда и только тогда , когда аффинно независимы.${\displaystyle \mathbb {R} ^{n}}$${\textstyle A_{0},A_{1},\ldots ,A_{n}}$${\textstyle A'_{0},A'_{1},\ldots ,A'_{n}}$${\displaystyle T:\mathbb {R} ^{n}\to \mathbb {R} ^{n}}$${\displaystyle T(A_{k})=A'_{k}}$${\displaystyle k=0,\cdots ,n}$${\displaystyle T}$${\displaystyle CM(P_{0},\cdots ,P_{n})\neq 0}$${\textstyle A_{0},A_{1},\ldots ,A_{n}}$

Встраивание и точки ${\displaystyle n+2}$${\displaystyle n+3}$[ править ]

Если точки могут быть вложены в as , то, кроме указанных выше условий, дополнительное необходимое условие состоит в том, что -симплекс, образованный , должен иметь безразмерный объем. То есть .${\displaystyle n+2}$${\displaystyle P_{0},\cdots ,P_{n+1}}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle A_{0},\cdots ,A_{n+1}}$${\displaystyle (n+1)}$${\textstyle A_{0},A_{1},\ldots ,A_{n+1}}$${\displaystyle (n+1)}$${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+1})=0}$

Верно и обратное. То есть, если для всех ,${\displaystyle k=1,\cdots ,n}$

${\displaystyle (-1)^{k+1}CM(P_{0},\cdots ,P_{k})\geq 0}$,

и

${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+1})=0}$,

тогда такое вложение существует.

Для вложения точек в необходимые и достаточные условия аналогичны:${\displaystyle n+3}$${\displaystyle \mathbb {R} ^{n}}$

1. Для всех , ;${\displaystyle k=1,\cdots ,n}$${\displaystyle (-1)^{k+1}CM(P_{0},\cdots ,P_{k})\geq 0}$
2. ${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+1})=0}$;
3. ${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+2})=0}$;
4. ${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+1},P_{n+2})=0}$.

Встраивание произвольного количества точек [ править ]

В общем, случая оказалось достаточно.${\displaystyle n+3}$

В целом, учитывая полуметрика пространство , оно может быть изометрически вложено в тогда и только тогда , когда существует такое , что для всех , и для любого ,${\displaystyle (R,d)}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle P_{0},\cdots ,P_{n}\in R}$${\displaystyle k=1,\cdots ,n}$${\displaystyle (-1)^{k+1}CM(P_{0},\cdots ,P_{k})\geq 0}$${\displaystyle P_{n+1},P_{n+2}\in R}$

1. ${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+1})=0}$;
2. ${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+2})=0}$;
3. ${\displaystyle CM(P_{0},\cdots ,P_{n},P_{n+1},P_{n+2})=0}$.

И такое вложение уникально с точностью до изометрии в .${\displaystyle \mathbb {R} ^{n}}$

Далее, если , то он не может быть изометрически вложен ни в какую . И такое вложение уникально с точностью до единственной изометрии в .${\displaystyle CM(P_{0},\cdots ,P_{n})\neq 0}$${\displaystyle \mathbb {R} ^{m},m<n}$${\displaystyle \mathbb {R} ^{n}}$

Таким образом, определители Кэли – Менгера дают конкретный способ вычислить, может ли полуметрическое пространство быть вложено в какое-то конечное пространство , и если да, то в какое минимальное пространство .${\displaystyle \mathbb {R} ^{n}}$${\displaystyle n}$${\displaystyle n}$

Приложения [ править ]

Есть много применений дистанционной геометрии. ^[3]

В телекоммуникационных сетях, таких как GPS , известны положения некоторых датчиков (которые называются якорями), а также известны некоторые расстояния между датчиками: проблема состоит в том, чтобы идентифицировать положения для всех датчиков. ^[5] Гиперболическая навигация - это одна из технологий, предшествующих GPS, которая использует геометрию расстояния для определения местоположения судов в зависимости от времени, которое требуется сигналам для достижения якорей.

В химии много применений. ^{[4] [12]} Такие методы, как ЯМР, могут измерять расстояния между парами атомов данной молекулы, и проблема состоит в том, чтобы вывести трехмерную форму молекулы на основе этих расстояний.

Некоторые программные пакеты для приложений:

• ДГСОЛ . Решает задачи геометрии на больших расстояниях при моделировании макромолекул .
• Xplor-NIH . На основе X-PLOR для определения структуры молекул на основе данных экспериментов ЯМР. Он решает проблемы дистанционной геометрии с помощью эвристических методов (таких как Simulated Annealing ) и методов локального поиска (таких как Conjugate Gradient Minimization ).
• ТИНКЕР . Молекулярное моделирование и дизайн. Он может решать задачи геометрии расстояния.
• SNLSDPclique . Код MATLAB для определения местоположения датчиков в сети датчиков на основе расстояний между датчиками.

См. Также [ править ]

• Матрица евклидовых расстояний
• Многомерное масштабирование (статистический метод, используемый, когда расстояния измеряются со случайными ошибками)
• Метрическое пространство
• Формула Тартальи
• Триангуляция
• Трилатерация

Ссылки [ править ]