Клотоида является кривой, кривизна изменяется линейно с его длиной кривой (кривизна кругового кривого равна обратной величиной радиуса). Эйлера спирали также часто называют СПИРОС , клотоидами или спирали Корня .
Спирали Эйлера находят применение в дифракционных вычислениях. Они также широко используются в качестве переходных кривых в железнодорожном и дорожном строительстве для соединения и перехода геометрии между касательной и круговой кривой. Аналогичное применение также можно найти в фотонных интегральных схемах . Принцип линейного изменения кривизны переходной кривой между касательной и круговой кривой определяет геометрию спирали Эйлера:
- Его кривизна начинается с нуля на прямом участке (касательной) и линейно увеличивается с длиной кривой.
- Там, где спираль Эйлера встречается с круговой кривой, ее кривизна становится равной кривизне последней.
Приложения [ править ]
Кривая перехода трека [ править ]

Чтобы двигаться по круговой траектории, объект должен подвергаться центростремительному ускорению (например: Луна вращается вокруг Земли из-за силы тяжести; автомобиль поворачивает свои передние колеса внутрь, чтобы создать центростремительную силу). Если транспортное средство, движущееся по прямой траектории, внезапно перейдет на тангенциальную круговую траекторию, это потребует внезапного переключения центростремительного ускорения в точке касания с нуля на требуемое значение; Этого было бы трудно достичь (представьте себе водителя, который мгновенно переводит рулевое колесо из прямого положения в поворотное, и автомобиль фактически делает это), оказывая механическую нагрузку на детали автомобиля и вызывая сильный дискомфорт (из-за бокового рывка ).
На ранних железных дорогах это мгновенное приложение поперечной силы не было проблемой, поскольку использовались низкие скорости и повороты с широким радиусом (поперечные силы на пассажиров и поперечный раскачивание были небольшими и допустимыми). По мере того как скорость рельсовых транспортных средств с годами увеличивалась, стало очевидно, что необходим сервитут, так что центростремительное ускорение увеличивается линейно с пройденным расстоянием. Учитывая выражение центростремительного ускоренияv 2/р, очевидным решением является создание кривой сервитута, кривизна которой 1/р, увеличивается линейно с пройденным расстоянием. Эта геометрия представляет собой спираль Эйлера.
Не зная о решении геометрии Леонарда Эйлера , Ренкин процитировал кубическую кривую (полиномиальная кривая степени 3), которая является приближением спирали Эйлера для небольших угловых изменений таким же образом, как парабола является приближением к круговой кривой. изгиб.
Мари Альфред Корню (а позже и несколько инженеров-строителей) также независимо решила исчисление спирали Эйлера. Спирали Эйлера в настоящее время широко используются в железнодорожном и автомобильном строительстве для обеспечения перехода или облегчения между касательной и горизонтальной круговой кривой.
Оптика [ править ]
Спираль Корню может использоваться для описания дифракционной картины. [1] Рассмотрим плоскую волну с амплитудой вектора E 0 e - jkz, которая дифрагирует на « острие » высотой h над x = 0 в плоскости z = 0 . Тогда поле дифрагированной волны можно выразить как
,
где Fr ( x ) - интегральная функция Френеля, которая образует спираль Корню на комплексной плоскости.
Итак, чтобы упростить расчет затухания плоской волны, когда она дифрагируется от острия ножа, можно использовать диаграмму спирали Корню, представив величины Fr ( a ) - Fr ( b ) как физические расстояния между представленными точками. на Fr ( a ) и Fr ( b ) для соответствующих a и b . Это облегчает грубое вычисление затухания плоской волны на острие высотой h в месте ( x , z ) за острием.
Интегрированная оптика [ править ]
Изгибы с непрерывно изменяющимся радиусом кривизны, следующие по спирали Эйлера, также используются для уменьшения потерь в фотонных интегральных схемах , либо в одномодовых волноводах , [2] [3] для сглаживания резких изменений кривизны и связи с модами излучения, либо в многомодовых волноводах , [4] , чтобы подавить связь с модами более высокого порядка и обеспечить эффективную одномодовую работу. Новаторское и очень элегантное применение спирали Эйлера к волноводам было сделано еще в 1957 году [5] с полым металлическим волноводом.для микроволн. Идея заключалась в том, чтобы использовать тот факт, что прямой металлический волновод можно физически согнуть, чтобы естественным образом принять форму постепенного изгиба, напоминающую спираль Эйлера.
Автогонки [ править ]
Писатель автоспорта Адам Бруйяр продемонстрировал использование спирали Эйлера для оптимизации гоночной трассы на участке входа в поворот. [6]
Типографика и цифровая векторная графика [ править ]
Raph Levien выпустил Spiro в качестве инструментария для дизайна кривых, особенно дизайна шрифтов, в 2007 году [7] [8] под свободной лицензией. Этот набор инструментов был довольно быстро реализован впоследствии в инструменте дизайна шрифтов Fontforge и в программе цифрового векторного рисования Inkscape .
Проекция карты [ править ]
Вырезание сферы по спирали шириной 1/Nи выравнивание получившейся формы дает спираль Эйлера, когда n стремится к бесконечности. [9] Если сфера является земным шаром , это создает проекцию карты , искажение которой стремится к нулю, когда n стремится к бесконечности. [10]
Формы усов [ править ]
Естественные формы вибрисс ( усов ) таинственной подушечки крысы хорошо аппроксимируются кусочками спирали Эйлера. Когда все эти части одной крысы собраны вместе, они охватывают интервал, простирающийся от одной спиральной области спирали Эйлера до другой. [11]
Формулировка [ править ]
Символы [ править ]
р Радиус кривизны R c Радиус круговой кривой на конце спирали θ Угол кривой от начала спирали (бесконечное R ) до определенной точки на спирали. Это также можно измерить как угол между начальной касательной и касательной в соответствующей точке.
θ с Угол полной спиральной кривой L , с Длина, измеренная по спиральной кривой от исходного положения L s , s o Длина спиральной кривой
| Вывод |
|---|
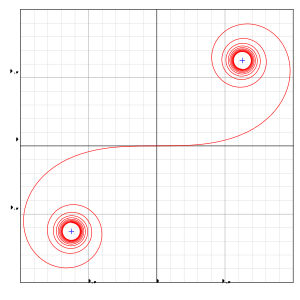
График справа иллюстрирует спираль Эйлера, используемую в качестве кривой сервитута (перехода) между двумя заданными кривыми, в данном случае прямой линией (отрицательная ось x ) и окружностью. Спираль начинается в начале координат в положительном направлении x и постепенно поворачивается против часовой стрелки, касаясь круга. Спираль представляет собой небольшой сегмент вышеупомянутой двухконцевой спирали Эйлера в первом квадранте.
|
Расширение интеграла Френеля [ править ]
Если a = 1 , что имеет место для нормализованной кривой Эйлера, то декартовы координаты задаются интегралами Френеля (или интегралами Эйлера):
Нормализация и заключение [ править ]
Для данной кривой Эйлера с:
или же
тогда
куда
Таким образом, процесс получения решения ( x , y ) спирали Эйлера можно описать как:
- Преобразуйте L исходной спирали Эйлера путем умножения с множителем a на L ' нормализованной спирали Эйлера;
- Найдите ( x ′, y ′) из интегралов Френеля; и
- Преобразуйте ( x ′, y ′) в ( x , y ) путем увеличения (денормализации) с фактором1/а. Обратите внимание, что1/а> 1 .
В процессе нормализации
потом
Обычно нормализация уменьшает L ' до небольшого значения (менее 1) и приводит к хорошим характеристикам сходимости интеграла Френеля, управляемому всего несколькими членами (ценой повышенной числовой нестабильности расчета, особенно для больших значений θ ). .
Иллюстрация [ править ]
Данный:
потом
и
Мы уменьшаем спираль Эйлера на √60 000 , то есть 100√ 6 , чтобы нормированная клотоидачто имеет:
и
Два угла θ s одинаковы. Таким образом, это подтверждает, что исходная и нормализованная спирали Эйлера геометрически подобны. Геометрическое место нормализованной кривой может быть определено с помощью интеграла Френеля, а геометрическое место исходной спирали Эйлера может быть получено путем увеличения или денормализации.
Другие свойства нормализованных спиралей Эйлера [ править ]
Нормализованные спирали Эйлера можно выразить как:
или выражается в виде степенного ряда :
Нормализованная спираль Эйлера в пределе сходится к одной точке, которую можно выразить как:
Нормализованные спирали Эйлера обладают следующими свойствами:
и
Обратите внимание, что 2 R c L s = 1 также означает1/R c= 2 L s , что согласуется с последним математическим утверждением.
Код для создания спирали Эйлера [ править ]
Следующий код SageMath создает второй график выше. Первые четыре строки выражают компонент спирали Эйлера. Функции Френеля найти не удалось. Вместо этого приняты интегралы двух расширенных рядов Тейлора. Остающийся код выражает, соответственно, касательную и окружность, включая вычисление координат центра.
var ( 'L' )p = интеграл ( taylor ( cos ( L ^ 2 ), L , 0 , 12 ), L ) q = интеграл ( taylor ( sin ( L ^ 2 ), L , 0 , 12 ), L ) r1 = параметрический_площадь ([ p , q ], ( L , 0 , 1 ), color = 'красный' ) r2 = строка ([( - 1.0 , 0 ), ( 0 , 0 )], rgbcolor = 'blue' ) х1 = р . сабвуферы ( L = 1 ) у1 = д . сабвуферы ( L = 1 ) R = 0,5 х2 = х1 - R * грех ( 1.0 ) у2 = у1 + R * cos ( 1,0 ) r3 = круг (( x2 , y2 ), R , rgbcolor = 'зеленый' ) показать ( r1 + r2 + r3 , aspect_ratio = 1 , axes = false ) Ниже приведен код на языке Wolfram Language для спирали Эйлера (или визуализация непосредственно в WolframAlpha ):
ParametricPlot [{ Sqrt [ Pi ] FresnelC [ t / Sqrt [ Pi ]], Sqrt [ Pi ] FresnelS [ t / Sqrt [ Pi ]]}, { t , -10 , 10 }]) В качестве альтернативы тот же результат может быть получен путем непосредственного решения дифференциального уравнения: [12]
ParametricPlot [ Вычислите [{ x [ s ], y [ s ]} /. DSolve [{ x ' [ s ] == Cos [ t [ s ]], y ' [ s ] == Sin [ t [ s ]], t ' [ s ] == s , x [ 0 ] == 0 , y [ 0 ] == 0 , t [ 0 ] == 0 }, { x , y , t }, s ]], { s , -10 , 10 }] Ниже приведен код Xcas для компонента спирали Эйлера:
plotparam ([int (cos (u ^ 2), u, 0, t), int (sin (u ^ 2), u, 0, t)], t, -4,4)
Ниже приведен код SageMath для полной двусторонней спирали Эйлера:
s = var ( 's' ) parametric_plot (( лямбда - ы : numerical_integral ( сов ( х ** 2 ), 0 , ев ) [ 0 ], лямбда - ы : numerical_integral ( грех ( х ** 2 ), 0 , ев ) [ 0 ]), ( - 3 * пи / 2 , 3 * пи / 2 )) Ниже приведен код JavaScript для рисования спирали Эйлера на элементе холста :
функция drawEulerSpiral ( холст , T , N , масштаб ) { ctx = canvas . getContext ( "2d" ); var dx , dy , t = 0 , prev = { x : 0 , y : 0 }, current ; var dt = T / N ; ctx . beginPath (); пока (N - ) { dx = Math . cos ( t * t ) * dt ; dy = Математика . грех ( т * т ) * дт ; t + = dt ; текущий = { x : пред . x + dx , y : пред . y + dy }; ctx . lineTo ( текущий. x * масштаб , ток . y * масштаб ); пред = текущий ; } ctx . ход (); } drawEulerSpiral ( document . getElementById ( "myCanvas" ), 10 , 10000 , 100 )Ниже приведен код логотипа (языка программирования) для рисования спирали Эйлера с использованием спрайта черепахи.
rt 90 repeat 720 [ fd 10 lt repcount ]См. Также [ править ]
- Архимедова спираль
- Интеграл Френеля
- Геометрический дизайн дорог
- Список спиралей
- Кривая перехода трека
Ссылки [ править ]
Заметки [ править ]
- ^ Юджин Хехт (1998). Оптика (3-е изд.). Эддисон-Уэсли. п. 491. ISBN. 978-0-201-30425-1.
- ^ Кохтоку, М .; и другие. (7 июля 2005 г.). «Новые методы изготовления волноводов для ПЛК следующего поколения» (PDF) . Технический обзор NTT . 3 (7): 37–41 . Проверено 24 января 2017 года .
- ^ Ли, G .; и другие. (11 мая 2012 г.). «Маршрутизация оптических волноводов SOI со сверхнизкими потерями и высокой плотностью для межсоединений макрочипов» . Оптика Экспресс . 20 (11): 12035–12039. DOI : 10,1364 / OE.20.012035 . PMID 22714189 .
- ^ Черчи, М .; и другие. (18 июля 2013 г.). «Резкое уменьшение размеров изгибов волновода на кремниевой фотонной платформе микронного масштаба». Оптика Экспресс . 21 (15): 17814–17823. arXiv : 1301.2197 . DOI : 10,1364 / OE.21.017814 . PMID 23938654 .
- ↑ Унгер, HG (сентябрь 1957 г.). «Изгибы нормальной моды для круговых электрических волн». Технический журнал Bell System . 36 (5): 1292–1307. DOI : 10.1002 / j.1538-7305.1957.tb01509.x .
- ^ Разработка, Paradigm Shift Driver; Бруйяр, Адам (18 марта 2016 г.). Идеальный поворот: пошаговое руководство для водителя по поиску оптимальной линии с помощью физики гонок . Книги о смене парадигмы автоспорта. ISBN 9780997382426.
- ^ http://levien.com/spiro/
- ^ http://www.typophile.com/node/33531
- ^ Бартольди, Лоран; Энрикес, Андре (2012). «Апельсиновые корки и интегралы Френеля». Математический интеллигент . 34 (3): 1–3. arXiv : 1202.3033 . DOI : 10.1007 / s00283-012-9304-1 . ISSN 0343-6993 .
- ^ "Странная проекция карты (Спираль Эйлера) - Numberphile" .
- ^ Старостин, Е.Л .; и другие. (15 января 2020 г.). "Спираль Эйлера крысиных усов" . Наука продвигается . 6 (3): eaax5145. DOI : 10.1126 / sciadv.aax5145 .
- Перейти ↑ Wolfram Research (1991). «DSolve - документация на языке Wolfram Language» . reference.wolfram.com .
Источники [ править ]
Дальнейшее чтение [ править ]
- Келлог, Норман Бенджамин (1907). Кривая перехода или Кривая регулировки (3-е изд.). Нью-Йорк: Макгроу.
- Вайсштейн, Эрик В. "Спираль Корню" . MathWorld .
- Р. Нэйв , Спираль Корню , Гиперфизика (2002) (Использует πt² / 2 вместо t².)
- Милтон Абрамовиц и Ирен А. Стегун, ред. Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Дувр, 1972 г. (см. Главу 7)
- "Петли для американских горок" . Проверено 12 ноября 2010 .
Внешние ссылки [ править ]
- Спираль Эйлера на 2-мерных математических кривых
- Интерактивный пример с JSXGraph
- Спиральная картографическая проекция Эйлера







![{\ displaystyle {\ begin {align} x & = \ int _ {0} ^ {L} \ cos \ theta \, ds \\ & = \ int _ {0} ^ {L} \ cos \ left [\ left ( как \ right) ^ {2} \ right] \, ds \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d6894160310c2dad25fe5df9c196adf90b4a66)


![{\ displaystyle {\ begin {align} x & = {\ frac {1} {a}} \ int _ {0} ^ {L '} \ cos \ left (s ^ {2} \ right) \, ds \\ y & = \ int _ {0} ^ {L} \ sin \ theta \, ds \\ & = \ int _ {0} ^ {L} \ sin \ left [\ left (как \ right) ^ {2} \ right] \, ds \\ & = {\ frac {1} {a}} \ int _ {0} ^ {L '} \ sin \ left ({s} ^ {2} \ right) \, ds \ end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d084f4ee394a4410eaeddb9ea46f180f255ba1eb)

















