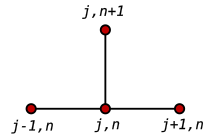
Метод конечных разностей
В численном анализе конечно - разностные методы ( FDM ) представляют собой класс численных методов для решения дифференциальных уравнений путем аппроксимации производных с конечными разностями . И пространственная область, и временной интервал (если применимо) дискретизируются или разбиваются на конечное число шагов, а значение решения в этих дискретных точках аппроксимируется путем решения алгебраических уравнений, содержащих конечные разности и значения из соседних точек.
Методы конечных разностей преобразуют обыкновенные дифференциальные уравнения (ODE) или уравнения в частных производных (PDE), которые могут быть нелинейными , в систему линейных уравнений , которые можно решить методами матричной алгебры. Современные компьютеры могут эффективно выполнять эти вычисления линейной алгебры , что, наряду с их относительной простотой реализации, привело к широкому использованию FDM в современном численном анализе. [1] На сегодняшний день FDM являются одним из наиболее распространенных подходов к численному решению PDE, наряду с методами конечных элементов . [1]
Во-первых, если предположить, что функция, производные которой должны быть аппроксимированы, ведет себя правильно, по теореме Тейлора мы можем создать разложение в ряд Тейлора
где н ! обозначает факториал n , а R n ( x ) является остаточным членом, обозначающим разницу между полиномом Тейлора степени n и исходной функцией. Мы получим приближение для первой производной функции «f», сначала усекая полином Тейлора:
Предполагая, что это достаточно мало, приближение первой производной от «f»:
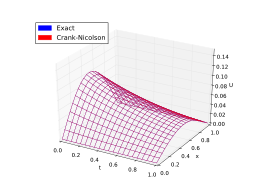
Погрешность решения метода определяется как разница между аппроксимацией и точным аналитическим решением. Двумя источниками ошибок в методах конечных разностей являются ошибка округления, потеря точности из-за компьютерного округления десятичных величин, и ошибка усечения или ошибка дискретизации , разница между точным решением исходного дифференциального уравнения и точной величиной, предполагающей совершенная арифметика (то есть без округления).