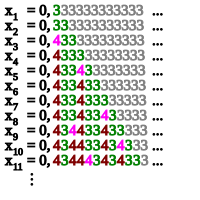
В теории вычислимости , последовательность Шпекера является вычислимой , монотонно возрастающая , ограниченная последовательность из рациональных чисел , чьи супремумом не вычислимая вещественное число . Первый пример такой последовательности был построен Эрнстом Спекером (1949).
Существование последовательностей Спекера имеет последствия для вычислимого анализа . Тот факт, что такие последовательности существуют, означает, что набор всех вычислимых действительных чисел не удовлетворяет принципу наименьшей верхней границы реального анализа, даже при рассмотрении только вычислимых последовательностей. Обычный способ решить эту проблему - рассматривать только последовательности, которые сопровождаются модулем сходимости ; никакая последовательность Шпекера не имеет вычислимого модуля сходимости. В более общем смысле последовательность Шпекера называется рекурсивным контрпримером к принципу наименьшей верхней границы, т. Е. Конструкцией, которая показывает, что эта теорема неверна при ограничении вычислимыми действительными числами.
Принцип наименьшей верхней границы также был проанализирован в программе обратной математики , где была определена точная сила этого принципа. В терминологии этой программы принцип наименьшей верхней границы эквивалентен ACA 0 над RCA 0 . Фактически, доказательство прямой импликации, т. Е. Того, что принцип наименьшей верхней границы влечет ACA 0 , легко получается из хрестоматийного доказательства (см. Simpson, 1999) невычислимости супремума в принципе наименьшей верхней границы.
Строительство [ править ]
Следующая конструкция описана Кушнером (1984). Пусть A - любое рекурсивно перечислимое множество натуральных чисел , которое не является разрешимым , и пусть ( a i ) - вычислимое перечисление A без повторений. Определите последовательность ( q n ) рациональных чисел с помощью правила
Ясно, что каждое q n неотрицательно и рационально, а последовательность q n строго возрастает. Более того, поскольку a i не имеет повторений, можно оценить каждое q n по ряду
Таким образом, последовательность ( q n ) ограничена сверху числом 1. Классически это означает, что q n имеет верхнюю грань x .
Показано, что x не вычислимое действительное число. Доказательство использует частный факт о вычислимых действительных числах. Если бы x был вычислимым, то существовала бы вычислимая функция r ( n ) такая, что | q j - q i | <1 / n для всех i , j > r ( n ). Чтобы вычислить r , сравните двоичное расширение x с двоичным расширением q i для все больших и больших значений i . Определение q iзаставляет одну двоичную цифру переходить от 0 до 1 каждый раз, когда i увеличивается на 1. Таким образом, будет некоторое n, где достаточно большой начальный сегмент x уже был определен q n, чтобы никакие дополнительные двоичные цифры в этом сегменте никогда не могли быть включен, что приводит к оценке расстояния между q i и q j для i , j > n .
Если какой - либо такая функция г , был вычислимы, это привело бы к процедуре принятия решения для A , следующим образом . Учитывая входной k , вычислите r (2 k +1 ). Если бы k появилось в последовательности ( a i ), это привело бы к увеличению последовательности ( q i ) на 2 - k -1 , но этого не может произойти, если все элементы ( q i ) находятся в пределах 2 - k - 1 друг друга. Таким образом, если к собирается быть перечислены в виде I, он должен быть пронумерован для значения i меньше r (2 k +1 ). Это оставляет конечное число возможных мест, где можно было бы перечислить k . Чтобы завершить процедуру принятия решения, проверьте их эффективным образом и верните 0 или 1 в зависимости от того, найдено ли k .
См. Также [ править ]
Ссылки [ править ]
- Дуглас Бриджес и Фред Ричман. Разновидности конструктивной математики, Оксфорд, 1987.
- Б. А. Кушнер (1984), Лекции по конструктивному математическому анализу , Американское математическое общество, Переводы математических монографий т. 60.
- Якоб Г. Симонсен (2005), «Повторение последовательностей Шпекера», Mathematical Logic Quarterly , т. 51, стр. 532–540. DOI : 10.1002 / malq.200410048
- С. Симпсон (1999), Подсистемы арифметики второго порядка , Springer.
- Э. Спекер (1949), "Nicht konstruktiv beweisbare Sätze der Analysis", Журнал символической логики , т. 14, стр. 145–158.

