Центрированный многоугольный номер

В центрированных многоугольных числах представляют собой класс серии из фигурных номеров , каждый из которых образован центральной точки, в окружении полигональных слоев с постоянным числом сторон. Каждая сторона многоугольного слоя содержит на одну точку больше, чем сторона в предыдущем слое, поэтому, начиная со второго многоугольного слоя, каждый слой с центрированным k -угольным числом содержит на k точек больше, чем предыдущий слой.

Примеры [ править ]

Каждый элемент в последовательности кратен предыдущему треугольному числу плюс 1. Это можно формализовать уравнением, где a - количество сторон многоугольника, а x - порядковый номер, начиная с нуля для начального 1. Для Например, центрированные квадратные числа в четыре раза больше треугольных чисел плюс 1 или эквивалентно . ${\displaystyle {\frac {ax(x+1)}{2}}+1}$${\displaystyle {\frac {4x(x+1)}{2}}+1}$

Эти серии состоят из

• центрированные треугольные числа 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, ... ( OEIS :  A005448 )
• квадратные числа с центрированием 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, ... ( OEIS :  A001844 )
• пятиугольные числа с центрированием 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, ... ( OEIS :  A005891 )
• центрированные шестиугольные числа 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, ... ( OEIS :  A003215 ), которые являются точной разницей последовательных кубов, т.е. x ³ - ( х - 1) ³
• центрированные семиугольные числа 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, ... ( OEIS :  A069099 )
• центрированные восьмиугольные числа 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, ... ( OEIS :  A016754 ), которые являются в точности нечетными квадратами
• центрированные неугольные числа 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, ... ( OEIS :  A060544 ), которые включают все четные совершенные числа, кроме 6
• центрированные десятиугольные числа 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, ... ( OEIS :  A062786 )
• шестигранные числа по центру: 1, 12, 34, 67, 111, 166, 232, 309, 397, 496, 606, 727, ... ( OEIS :  A069125 )
• центрированные двенадцатиугольные числа 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, ... ( OEIS :  A003154 ), которые также являются звездными числами

и так далее.

На следующих диаграммах показано несколько примеров центрированных многоугольных чисел и их геометрическое построение. Сравните эти диаграммы с диаграммами в многоугольном числе .

центрированное треугольное число	число в центре квадрата	центрированное пятиугольное число	центрированное шестиугольное число

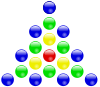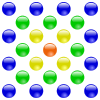Центрированные квадратные числа [ править ]

Центрированные шестиугольные числа [ править ]

Формула [ править ]

Как видно из приведенных выше диаграмм, n- е центральное k -угольное число может быть получено путем размещения k копий ( n -1) -го треугольного числа вокруг центральной точки; следовательно, n- е центральное k -угольное число может быть математически представлено как

${\displaystyle C_{k,n}={\frac {kn}{2}}(n-1)+1.}$

Разность n -го и ( n +1) -го последовательных центрированных k -угольных чисел равна k (2 n +1).

П -х по центру K -gonal число равно п -му регулярный K -gonal числа плюс ( п -1) ² .

Как и в случае с правильными многоугольными числами, первое центрированное k -угольное число равно 1. Таким образом, для любого k , 1 одновременно является k -угольным и центрированным k -угольным. Следующее число, которое должно быть как k -угольным, так и центрированным k -угольным, можно найти по формуле:

${\displaystyle {\frac {k^{2}}{2}}(k-1)+1}$

что говорит нам, что 10 одновременно является треугольным и центрированным треугольником, 25 - квадратным и центрированным квадратом и т. д.

В то время как простое число p не может быть многоугольным числом (за исключением тривиального случая, т. Е. Каждое p является вторым p -угольным числом), многие центрированные многоугольные числа являются простыми числами. Фактически, если k ≥ 3, k ≠ 8, k ≠ 9, то существует бесконечно много центрированных k -угольных чисел, которые являются простыми числами (в предположении гипотезы Буняковского ). (Поскольку все центрированные восьмиугольные числа также являются квадратными числами , а все центрированные неугольные числа также являются треугольными числами (и не равно 3), поэтому оба они не могут быть простыми числами)

Sum of Reciprocals [ править ]

Сумма из обратных для центрированного K -gonal чисел ^[1]

${\displaystyle {\frac {2\pi }{k{\sqrt {1-{\frac {8}{k}}}}}}\tan \left({\frac {\pi }{2}}{\sqrt {1-{\frac {8}{k}}}}\right)}$, если k ≠ 8

${\displaystyle {\frac {\pi ^{2}}{8}}}$, если k = 8

Ссылки [ править ]

• Нил Слоан и Саймон Плафф (1995).Энциклопедия целочисленных последовательностей. Сан-Диего: Academic Press.: Рис. M3826
• Вайсштейн, Эрик В. "Центрированное многоугольное число" . MathWorld .
• Ф. Тэпсон (1999). Оксфордский словарь изучения математики (2-е изд.). Издательство Оксфордского университета. С. 88–89. ISBN 0-19-914-567-9.