Дополнение (теория множеств)

… Тогда дополнение к A - это все остальное.

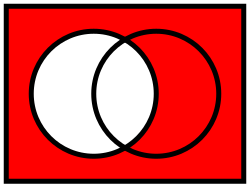
В теории множеств , то дополнение из множества A , часто обозначают A ^с (или А ' ), ^{[1] [2]} являются элементы не в A . ^[3]

Когда все рассматриваемые множества считаются подмножества данного множества U , то абсолютное дополнение в A есть множество элементов U , но не в A .

Относительное дополнение в А относительно множества В , называемый также множество различий в B и A , написанный B \ , есть множество элементов в B , но не в A . ^[1]

Абсолютное дополнение [ править ]

Абсолютное дополнение в А (левый круг) в U : .${\displaystyle A^{c}=U\setminus A}$

Определение [ править ]

Если A - это набор, то абсолютное дополнение к A (или просто дополнение к A ) - это набор элементов, не входящих в A (внутри большего набора, который неявно определен). Другими словами, пусть U - множество, содержащее все изучаемые элементы; если нет необходимости упоминать U , либо потому, что он был ранее указан, либо потому, что он очевиден и уникален, то абсолютное дополнение к A является относительным дополнением к A в U : ^[4]

${\displaystyle A^{c}=U-A}$.

Или формально:

${\displaystyle A^{c}=\{x\in U\mid x\notin A\}.}$

Абсолютное дополнение к A обычно обозначается A ^c . ^[1] Другие обозначения включают в себя , , ^[3] , и . ^[5]${\displaystyle {\overline {A}}}$ ${\displaystyle A'}$ ${\displaystyle \complement _{U}A}$${\displaystyle \complement A}$

Примеры [ править ]

• Предположим, что вселенная - это набор целых чисел . Если A - это набор нечетных чисел, то дополнение к A - это набор четных чисел. Если B - это набор, кратный 3, то дополнение к B - это набор чисел, конгруэнтных 1 или 2 по модулю 3 (или, проще говоря, целым числам, не кратным 3).
• Предположим, что Вселенная представляет собой стандартную колоду из 52 карт . Если набор A - масть пик, то дополнение к A - это объединение мастей треф, бубен и червей. Если набор B является объединением мастей треф и бубен, то набор B является объединением мастей червей и пиков.

Свойства [ править ]

Пусть и B два множества во вселенной U . Следующие идентичности отражают важные свойства абсолютных дополнений:

Законы Де Моргана : ^[6]

• ${\displaystyle \left(A\cup B\right)^{c}=A^{c}\cap B^{c}.}$
• ${\displaystyle \left(A\cap B\right)^{c}=A^{c}\cup B^{c}.}$

Дополняющие законы: ^[6]

• ${\displaystyle A\cup A^{c}=U.}$
• ${\displaystyle A\cap A^{c}=\varnothing .}$
• ${\displaystyle \varnothing ^{c}=U.}$
• ${\displaystyle U^{c}=\varnothing .}$
• ${\displaystyle {\text{If }}A\subseteq B{\text{, then }}B^{c}\subseteq A^{c}.}$

  (это следует из эквивалентности условного выражения и его контрпозитива ).

Закон инволюции или двойного дополнения:

• ${\displaystyle \left(A^{c}\right)^{c}=A.}$

Отношения между относительными и абсолютными дополнениями:

• ${\displaystyle A\setminus B=A\cap B^{c}.}$
• ${\displaystyle (A\setminus B)^{c}=A^{c}\cup B=A^{c}\cup (B\cap A).}$

Связь с установленной разницей:

• ${\displaystyle A^{c}\setminus B^{c}=B\setminus A.}$

Первые два закона дополняют приведенные выше , показывают , что если не является пустым, собственное подмножество из U , то { , ^с } представляет собой разбиение на U .

Относительное дополнение [ править ]

Определение [ править ]

Если и B являются множествами, то относительное дополнение из A в B , ^[6] также называют разницу набор из B и A , ^[7] представляет собой набор элементов в B , но не в A .

Относительное дополнение в А (левый круг) в B (правый круг):${\displaystyle B\cap A^{c}=B\setminus A}$

Относительное дополнение A в B обозначается B ∖ A в соответствии со стандартом ISO 31-11 . Это иногда пишется B - A , ^[1] , но это обозначение является неоднозначным, как и в некоторых контекстах это может быть интерпретировано как множество всех элементов Ь - , где б берется из B и из A .

Формально:

${\displaystyle B\setminus A=\{x\in B\mid x\notin A\}.}$

Примеры [ править ]

• ${\displaystyle \{1,2,3\}\setminus \{2,3,4\}=\{1\}}$.
• ${\displaystyle \{2,3,4\}\setminus \{1,2,3\}=\{4\}}$.
• Если - множество действительных чисел и - множество рациональных чисел , то - множество иррациональных чисел .${\displaystyle \mathbb {R} }$${\displaystyle \mathbb {Q} }$${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$

Свойства [ править ]

Пусть A , B и C - три множества. Следующие идентичности отражают примечательные свойства относительных дополнений:

• ${\displaystyle C\setminus (A\cap B)=(C\setminus A)\cup (C\setminus B)}$.
• ${\displaystyle C\setminus (A\cup B)=(C\setminus A)\cap (C\setminus B)}$.
• ${\displaystyle C\setminus (B\setminus A)=(C\cap A)\cup (C\setminus B)}$,

  с важным частным случаем, демонстрирующим, что пересечение может быть выражено только с помощью операции относительного дополнения.${\displaystyle C\setminus (C\setminus A)=(C\cap A)}$

• ${\displaystyle (B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A)}$.
• ${\displaystyle (B\setminus A)\cup C=(B\cup C)\setminus (A\setminus C)}$.
• ${\displaystyle A\setminus A=\emptyset }$.
• ${\displaystyle \emptyset \setminus A=\emptyset }$.
• ${\displaystyle A\setminus \emptyset =A}$.
• ${\displaystyle A\setminus U=\emptyset }$.

Дополнительное отношение [ править ]

Бинарное отношение R определяется как подмножество произведение множеств Х × Y . Дополняют друг друга отношение есть множество дополнение R в X × Y . Дополнение отношения R можно записать${\displaystyle {\bar {R}}}$

${\displaystyle {\bar {R}}\ =\ (X\times Y)\setminus R.}$

Здесь, R часто рассматривается в качестве логической матрицы с рядами , представляющие элементы X , а столбцы элементов Y . Истина aRb соответствует 1 в строке a , столбце b . Создание дополнительного отношения к R соответствует переключению всех единиц на 0 и 0 на 1 для логической матрицы дополнения.

Вместе с составом отношений и обратных связей , взаимодополняющих отношений и алгеброй множеств являются элементарными операциями по исчислению отношений .

Обозначение LaTeX [ править ]

В языке набора LaTeX команда \setminus^[8] обычно используется для визуализации установленного символа различия, который похож на символ обратной косой черты . При рендеринге \setminusкоманда выглядит идентично \backslash, за исключением того, что перед ней и за косой чертой немного больше места, как в последовательности LaTeX \mathbin{\backslash}. Вариант \smallsetminusдоступен в пакете amssymb.

На языках программирования [ править ]

Некоторые языки программирования имеют наборы встроенных структур данных . Такая структура данных ведет себя как конечный набор , то есть она состоит из конечного числа данных, которые не упорядочены специально и, таким образом, могут рассматриваться как элементы набора. В некоторых случаях элементы не обязательно должны быть разными, и структура данных кодирует мультимножества, а не наборы. В этих языках программирования есть операторы или функции для вычисления дополнительных и установленных различий.

Эти операторы могут обычно применяться также к структурам данных, которые на самом деле не являются математическими наборами, такими как упорядоченные списки или массивы . Отсюда следует, что некоторые языки программирования могут иметь вызываемую функцию set_difference, даже если у них нет никакой структуры данных для наборов.

См. Также [ править ]

• Алгебра множеств
• Пересечение (теория множеств)
• Список установленных идентичностей и отношений
• Наивная теория множеств
• Симметричная разница
• Союз (теория множеств)

Примечания [ править ]

Ссылки [ править ]

• Бурбаки, Н. (1970). Теория ансамблей (на французском языке). Пэрис: Германн. ISBN 978-3-540-34034-8.
• Девлин, Кейт Дж. (1979). Основы современной теории множеств . Universitext. Springer . ISBN 0-387-90441-7. Zbl  0407.04003 .
• Халмос, Пол Р. (1960). Теория наивных множеств . Университетская серия по математике. Компания ван Ностранд. Zbl  0087.04403 .

Внешние ссылки [ править ]

• Вайсштейн, Эрик В. «Дополнение» . MathWorld .
• Вайсштейн, Эрик В. «Дополнительный набор» . MathWorld .