Диаграмма Кокстера – Дынкина

Диаграммы Кокстера – Дынкина для фундаментальных конечных групп Кокстера

Диаграммы Кокстера – Дынкина для фундаментальных аффинных групп Кокстера

В геометрии , A - схема Кокстера-Дынкина (или Косетер - схема , граф Кокстера ) представляет собой график , с числовым программным помеченными ребрами ( так называемых ветвями ) , представляющих собой пространственные отношения между коллекцией зеркал (или отражающими гиперплоскостями ). Он описывает калейдоскопическую конструкцию: каждый «узел» графа представляет собой зеркало ( фасет домена ), а метка, прикрепленная к ветви, кодирует порядок двугранного угла между двумя зеркалами (на гребне домена), то есть величина, на которую можно умножить угол между отражающими плоскостями, чтобы получить 180 градусов. Непомеченная ветвь неявно представляет третий порядок (60 градусов).

Каждая диаграмма представляет группу Кокстера , а группы Кокстера классифицируются по соответствующим диаграммам.

Диаграммы Дынкина являются тесно связанными объектами, которые отличаются от диаграмм Кокстера в двух отношениях: во-первых, ветви с меткой «4» и выше являются направленными , а диаграммы Кокстера - неориентированными ; во-вторых, диаграммы Дынкина должны удовлетворять дополнительному ( кристаллографическому ) ограничению, а именно, что единственными разрешенными метками ветвлений являются 2, 3, 4 и 6. Диаграммы Дынкина соответствуют и используются для классификации корневых систем и, следовательно, полупростых алгебр Ли . ^[1]

Описание [ править ]

Ветви диаграммы Кокстера – Дынкина помечены рациональным числом p , представляющим двугранный угол 180 ° / p . Когда $p = 2,$ угол равен 90 ° и зеркала не взаимодействуют друг с другом, поэтому ветвь на диаграмме можно не указывать. Если ветка не помечена, предполагается, что она имеет $p = 3$ , что соответствует углу 60 °. Два параллельных зеркала имеют ответвление, отмеченное знаком «∞». В принципе, n зеркал можно представить в виде полного графа, в котором все n ( $n - 1) / 2$ ветви нарисованы. На практике почти все интересные конфигурации зеркал включают ряд прямых углов, поэтому соответствующие ветви опускаются.

Диаграммы могут быть помечены их графической структурой. Первыми формами, изученными Людвигом Шлефли, являются ортосхемы, которые имеют линейные графы, порождающие правильные многогранники и правильные соты . Плагиосхемы - это симплексы, представленные графами ветвления, а циклохемы - это симплексы, представленные циклическими графами.

Матрица Шлефли [ править ]

Каждой диаграмме Кокстера соответствует матрица Шлефли (названная так в честь Людвига Шлефли ) с матричными элементами $a i, j = a j, i = -2cos (π / p),$ где p - порядок ветвления между парами зеркал. Как матрицу косинусов , она также называется матрицей Грамиана в честь Йоргена Педерсена Грама . Все матрицы Шлефли группы Кокстера симметричны, потому что их корневые векторы нормированы. Она тесно связана с матрицей Картана , используемой в аналогичных, но ориентированных диаграммах Дынкина. в ограниченных случаях p = 2, 3, 4 и 6, которые в общем случае НЕ симметричны.

Определитель матрицы Шлефли, называемый шлефлианом , и его знак определяют, является ли группа конечной (положительной), аффинной (нулевой), неопределенной (отрицательной). Это правило называется критерием Шлефли . ^[2]

Собственные значения матрицы Шлефли определяют, имеет ли группа Кокстера конечный тип (все положительные), аффинный тип (все неотрицательные, хотя бы одно из них равно нулю) или неопределенный тип (в противном случае). Неопределенный тип иногда дополнительно подразделяется, например, на гиперболические и другие группы Кокстера. Однако существует несколько неэквивалентных определений гиперболических групп Кокстера. Мы используем следующее определение: группа Кокстера со связной диаграммой является гиперболической, если она не имеет ни конечного, ни аффинного типа, но каждая собственная связная поддиаграмма имеет конечный или аффинный тип. Гиперболическая группа Кокстера компактна, если все подгруппы конечны (т. Е. Имеют положительные детерминанты) ипаракомпакт, если все его подгруппы конечны или аффинны (т. е. имеют неотрицательные детерминанты).

Конечные и аффинные группы также называются эллиптическими и параболическими соответственно. Гиперболические группы также называются Ланнером в честь Ф. Ланнера, который перечислил компактные гиперболические группы в 1950 г. ^[3], и Кошуля (или квази-Ланнера) для паракомпактных групп.

Группы Коксетеров 2-го ранга [ править ]

Для ранга 2 тип группы Кокстера полностью определяется определителем матрицы Шлефли, поскольку это просто произведение собственных значений: конечный тип (положительный определитель), аффинный тип (нулевой определитель) или гиперболический (отрицательный определитель) . Коксетер использует эквивалентную скобку, в которой перечислены последовательности порядков ветвления вместо графических диаграмм узел-ветвь. Рациональные решения [p / q],, также существуют с gcd (p, q) = 1, которые определяют перекрывающиеся фундаментальные области. Например, 3/2, 4/3, 5/2, 5/3, 5/4. и 6/5.

Тип	Конечный					Аффинный	Гиперболический
Геометрия					...
Coxeter	[]	[2]	[3]	[4]	[п]	[∞]	[∞]	[iπ / λ]
Приказ	2	4	6	8	2 шт.	∞
Зеркальные линии раскрашены в соответствии с узлами диаграммы Кокстера. Фундаментальные области окрашены попеременно.

Диаграммы групп Кокстера ранга 2
Заказать p	Группа	Диаграмма Кокстера		Матрица Шлефли
Заказать p	Группа	Диаграмма Кокстера		${\ displaystyle \ left [{\ begin {matrix} 2 & a_ {12} \\ a_ {21} & 2 \ end {matrix}} \ right]}$	Определитель (4-а ₂₁ * а ₁₂ )
Конечное (определитель> 0)
2	Я ₂ (2) = А ₁ хА ₁		[2]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & 0 \\ 0 & 2 \ end {smallmatrix}} \ right]}$	4
3	Я ₂ (3) = А ₂		[3]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & -1 \\ - 1 & 2 \ end {smallmatrix}} \ right]}$	3
3/2			[3/2]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & 1 \\ 1 & 2 \ end {smallmatrix}} \ right]}$	3
4	Я ₂ (4) = В ₂		[4]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & - {\ sqrt {2}} \\ - {\ sqrt {2}} & 2 \ end {smallmatrix}} \ right]}$	2
4/3			[4/3]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & {\ sqrt {2}} \\ {\ sqrt {2}} & 2 \ end {smallmatrix}} \ right]}$	2
5	I ₂ (5) = H ₂		[5]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & - \ phi \\ - \ phi & 2 \ end {smallmatrix}} \ right]}$	${\ displaystyle (5 - {\ sqrt {5}}) / 2}$ ~ 1,38196601125
5/4			[5/4]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & \ phi \\\ phi & 2 \ end {smallmatrix}} \ right]}$	${\ displaystyle (5 - {\ sqrt {5}}) / 2}$ ~ 1,38196601125
5/2			[5/2]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & 1- \ phi \\ 1- \ phi & 2 \ end {smallmatrix}} \ right]}$	${\ displaystyle (5 + {\ sqrt {5}}) / 2}$ ~ 3,61803398875
5/3			[5/3]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & \ phi -1 \\\ phi -1 & 2 \ end {smallmatrix}} \ right]}$	${\ displaystyle (5 + {\ sqrt {5}}) / 2}$ ~ 3,61803398875
6	I ₂ (6) = G ₂		[6]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & - {\ sqrt {3}} \\ - {\ sqrt {3}} & 2 \ end {smallmatrix}} \ right]}$	1
6/5			[6/5]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & {\ sqrt {3}} \\ {\ sqrt {3}} & 2 \ end {smallmatrix}} \ right]}$	1
8	Я ₂ (8)		[8]	${\ displaystyle \ left [{\ begin {smallmatrix} 2 & - {\ sqrt {2 + {\ sqrt {2}}}} \\ - {\ sqrt {2 + {\ sqrt {2}}}} & 2 \ end {smallmatrix}} \ right]}$	$2-{\sqrt {2}}$ ~ 0,58578643763
10	Я ₂ (10)		[10]	$\left[{\begin{smallmatrix}2&-{\sqrt {(5+{\sqrt {5}})/2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{smallmatrix}}\right]$	$(3-{\sqrt {5}})/2$ ~ 0,38196601125
12	Я ₂ (12)		[12]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {3}}}}\\-{\sqrt {2+{\sqrt {3}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {3}}$ ~ 0,26794919243
п	I ₂ (p)		[п]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /p)$
Аффинный (детерминант = 0)
∞	I ₂ (∞) = = ${\tilde {I}}_{1}$ ${\tilde {A}}_{1}$		[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
Гиперболический (детерминант≤0)
∞			[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
∞			[iπ / λ]	$\left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]$	$-4\sinh ^{2}(2\lambda )\leq 0$

Геометрические визуализации [ править ]

Диаграмму Кокстера – Дынкина можно рассматривать как графическое описание фундаментальной области зеркал. Зеркало представляет собой гиперплоскость в заданном сферическом, евклидовом или гиперболическом пространстве. (В 2D-пространстве зеркало - это линия, а в 3D-пространстве - это плоскость).

Эти визуализации показывают фундаментальные области для двумерных и трехмерных евклидовых групп и двумерных сферических групп. Для каждого из них диаграмма Кокстера может быть выведена путем идентификации зеркал гиперплоскости и маркировки их связности, игнорируя двугранные углы в 90 градусов (порядок 2).

Группы Кокстера на евклидовой плоскости с эквивалентными диаграммами. Отражения помечены как узлы графа R 1, R 2 и т. Д. И окрашены в соответствии с порядком их отражения. Отражения под углом 90 градусов неактивны и поэтому не отображаются на диаграмме. Параллельные зеркала соединяются ветвью с обозначением ∞. Призматическая группа x показана как удвоение , но также может быть создана как прямоугольные области путем удвоения треугольников. Это удвоение треугольника. ${\tilde {I}}_{1}$ ${\tilde {I}}_{1}$ ${\tilde {C}}_{2}$ ${\tilde {G}}_{2}$ ${\tilde {A}}_{2}$ ${\tilde {G}}_{2}$
Многие группы Кокстера в гиперболической плоскости могут быть расширены из евклидовых случаев как серии гиперболических решений.
Группы Кокстера в трехмерном пространстве с диаграммами. Зеркала (грани треугольника) помечены противоположной вершиной 0..3. Ветки раскрашены в порядке их отражения. заполняет 1/48 куба. заполняет 1/24 куба. заполняет 1/12 куба. ${\tilde {C}}_{3}$ ${\tilde {B}}_{3}$ ${\tilde {A}}_{3}$	Группы Кокстера на сфере с эквивалентными диаграммами. Одна фундаментальная область обведена желтым. Вершины домена (и ветви графа) окрашены в соответствии с порядком их отражения.

Конечные группы Кокстера [ править ]

Смотрите также семейства многогранников для получения таблицы однородных многогранников конечных узлов, связанных с этими группами.

Для одних и тех же групп даны три разных символа - буква / цифра, набор чисел в скобках и диаграмма Кокстера.
Разветвленные группы D _n представляют собой половину или альтернативную версию регулярных групп C _n .
Раздвоенные группы D _n и E _n также помечаются верхним индексом [3 ^{a , b , c} ], где a , b , c - номера сегментов в каждой из трех ветвей.

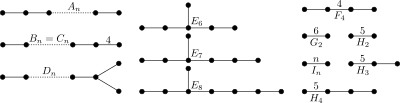
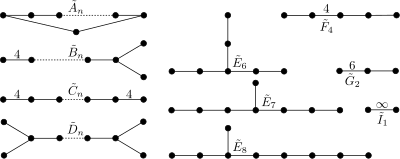
Связные конечные диаграммы Кокстера – Дынкина (ранги с 1 по 9)
Классифицировать	Простые группы Ли			Исключительные группы Ли
Классифицировать	${A}_{1+}$	${B}_{2+}$	${D}_{2+}$	E 3 − 8 {\displaystyle {E}_{3-8}}	F 3 − 4 {\displaystyle {F}_{3-4}}	G 2 {\displaystyle {G}_{2}}	${H}_{2-4}$	${I}_{2}(p)$
1	A ₁ = []
2	A ₂ = [3]	B ₂ = [4]	D ₂ = A ₁ A ₁			G ₂ = [6]	H ₂ = [5]	I ₂ [p]
3	A ₃ = [3 ² ]	B ₃ = [3,4]	D ₃ = A ₃	Е ₃ = А ₂ А ₁	F ₃ = B ₃		H ₃
4	A ₄ = [3 ³ ]	B ₄ = [3 ² , 4]	D ₄ = [3 ^1,1,1 ]	Е ₄ = А ₄	П ₄		H ₄
5	A ₅ = [3 ⁴ ]	B ₅ = [3 ³ , 4]	D ₅ = [3 ^2,1,1 ]	E ₅ = D ₅
6	A ₆ = [3 ⁵ ]	B ₆ = [3 ⁴ , 4]	D ₆ = [3 ^3,1,1 ]	E ₆ = [3 ^2,2,1 ]
7	A ₇ = [3 ⁶ ]	B ₇ = [3 ⁵ , 4]	D ₇ = [3 ^4,1,1 ]	E ₇ = [3 ^3,2,1 ]
8	A ₈ = [3 ⁷ ]	B ₈ = [3 ⁶ , 4]	D ₈ = [3 ^5,1,1 ]	E ₈ = [3 ^4,2,1 ]
9	A ₉ = [3 ⁸ ]	B ₉ = [3 ⁷ , 4]	D ₉ = [3 ^6,1,1 ]
10+	..	..	..	..

Приложение с однородными многогранниками [ править ]

При построении однородных многогранников узлы помечаются кольцом как активные , если образующая точка находится вне зеркала, создавая новое ребро между образующей точкой и ее зеркальным отображением. Узел без кольца представляет собой неактивное зеркало, которое не генерирует новых точек. Кольцо без узла называется отверстием .

Два ортогональных зеркала можно использовать для создания квадрата,

, видно здесь с красной точкой генератора и 3 виртуальными копиями через зеркала. В этом ортогональном случае генератор должен находиться вне обоих зеркал, чтобы создать интерьер. Кольцевая разметка предполагает, что активные кольца имеют генераторы на одинаковом расстоянии от всех зеркал, в то время как прямоугольник также может представлять неоднородное решение.

Диаграммы Кокстера – Дынкина могут явно перечислить почти все классы однородных многогранников и однородных мозаик . Каждый однородный многогранник с чистой отражательной симметрией (все, кроме нескольких частных случаев, имеют чистую отражательную симметрию) может быть представлен диаграммой Кокстера – Дынкина с перестановками разметок . Каждый однородный многогранник может быть сгенерирован с использованием таких зеркал и одной точки генератора: зеркальные изображения создают новые точки как отражения, затем края многогранника могут быть определены между точками и точкой зеркального отображения. Лицагенерируются повторным отражением кромки, в конечном итоге оборачивающейся вокруг исходного генератора; окончательная форма, как и любые грани более высокого измерения, аналогично создаются отражением лица, ограничивающим область.

Чтобы указать генерирующую вершину, один или несколько узлов помечаются кольцами, что означает, что вершина не находится на зеркале (ах), представленном кольцевым узлом (ами). (Если отмечены два или более зеркала, вершина находится на одинаковом расстоянии от них.) Зеркало активно (создает отражения) только по отношению к точкам, не находящимся на нем. Для представления многогранника диаграмме необходим хотя бы один активный узел. Несвязанная диаграмма (подгруппы, разделенные ветвями второго порядка или ортогональными зеркалами) требует по крайней мере одного активного узла в каждом подграфе.

Все правильные многогранники , представленные символом Шлефли { $p, q, r, ...$ }, могут иметь свои фундаментальные области, представленные набором из n зеркал с соответствующей диаграммой Кокстера – Дынкина, состоящей из линий узлов и ветвей, помеченных $p, q, r, ...,$ с окольцованным первым узлом.

Равномерные многогранники с одним кольцом соответствуют образующим в углах симплекса фундаментальной области. Два кольца соответствуют краям симплекса и имеют степень свободы, причем только средняя точка является однородным решением для равных длин ребер. Как правило, точки образующих k -кольцев находятся на (k-1) -гранях симплекса, и если все узлы окружены кольцами, точка образующих находится внутри симплекса.

Частный случай однородных многогранников с неотражающей симметрией представлен вторичной разметкой, в которой удаляется центральная точка кольцевого узла (так называемая дыра ). Эти формы представляют собой чередования ^{[ требуется пояснение ]} многогранников с отражающей симметрией, подразумевая, что альтернативные узлы удаляются ^{[ необходимо пояснение ]} . Полученный многогранник будет иметь подсимметрию исходной группы Кокстера . Усеченное чередование называется пренебрежительным .

Один узел представляет собой одно зеркало. Это называется группой A ₁ . Если обведено кружком, образуется сегмент линии, перпендикулярный зеркалу, представленный как {}.
Два незакрепленных узла представляют собой два перпендикулярных зеркала. Если оба узла обведены кружком, можно создать прямоугольник или квадрат, если точка находится на одинаковом расстоянии от обоих зеркал.
Два узла, присоединенные ветвью порядка n, могут создать n -угольник, если точка находится на одном зеркале, и 2 n -угольник, если точка находится вне обоих зеркал. Это образует группу I ₁ (n).
Два параллельных зеркала могут представлять собой группу бесконечных многоугольников I ₁ (∞), также называемую Ĩ ₁ .
Три зеркала в треугольнике образуют изображения, видимые в традиционном калейдоскопе, и могут быть представлены тремя узлами, соединенными в треугольник. В повторяющихся примерах ветви будут обозначены как (3 3 3), (2 4 4), (2 3 6), хотя последние два могут быть нарисованы в виде линии ( две ветви игнорируются). Это создаст однородные мозаики .
Три зеркала могут образовывать однородные многогранники ; включение рациональных чисел дает набор треугольников Шварца .
Три зеркала, одно из которых перпендикулярно двум другим, могут образовывать однородные призмы .

Внутри общего треугольника имеется 7 отражающих однородных конструкций, основанных на 7 положениях топологического генератора в основной области. Каждое активное зеркало формирует край, два активных зеркала имеют генераторы на сторонах домена, а три активных зеркала имеют генератор внутри. Одна или две степени свободы могут быть решены для уникального положения для равных длин ребер результирующего многогранника или мозаики.

Пример 7 генераторов с октаэдрической симметрией , треугольник фундаментальной области (4 3 2), с 8-м поколением курноса в качестве чередования

Двойники однородных многогранников иногда помечаются перпендикулярной косой чертой, заменяющей кольцевые узлы, и косой чертой для узловых отверстий курносых. Например,представляет собой прямоугольник (как два активных ортогональных зеркала), апредставляет собой двойной многоугольник , ромб .

Примеры многогранников и мозаик [ править ]

Например, у группы B ₃ Coxeter есть диаграмма:. Это также называется октаэдрической симметрией .

Есть 7 выпуклых однородных многогранников, которые могут быть построены из этой группы симметрий, и 3 из ее альтернирующих подсимметрий, каждый из которых имеет однозначно размеченную диаграмму Кокстера – Дынкина. Символ Wythoff представляет собой частный случай диаграммы Кокстера для графов ранга 3, с указанием всех трех порядков ветвлений, а не подавления ветвей порядка 2. Символ Wythoff может обрабатывать курносую форму, но не общие чередования, когда все узлы не обведены.

Однородные октаэдрические многогранники
Симметрия : [4,3], (* 432)							[4,3] ⁺ (432)	[1 ⁺ , 4,3] = [3,3] (* 332)		[3 ⁺ , 4] (3 * 2)
{4,3}	т {4,3}	г {4,3} г {3 ^1,1 }	т {3,4} т {3 ^1,1 }	{3,4} {3 ^1,1 }	rr {4,3} s ₂ {3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	ч 2 {4,3} т {3,3}	с {3,4} с {3 ^1,1 }

		знак равно	знак равно	знак равно				знак равно или же	знак равно или же	знак равно

Двойники к однородным многогранникам
V4 3	V3.8 2	В (3,4) 2	V4.6 2	V3 4	V3.4 3	V4.6.8	V3 4 .4	V3 3	V3.6 2	V3 5

Те же конструкции могут быть сделаны на разъединенных (ортогональных) кокстеровские группы , таких как единые призмы , и их можно увидеть более ясно , как замощения dihedrons и hosohedrons на сфере, как эта [6] × [] или [6,2] семья:

Однородные шестиугольные двугранные сферические многогранники
Симметрия : [6,2] , (* 622)							[6,2] ⁺ , (622)	[6,2 ⁺ ], (2 * 3)


{6,2}	т {6,2}	г {6,2}	т {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	с {2,6}
Двойники к униформе

V6 2	V12 2	V6 2	V4.4.6	V2 6	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Для сравнения, [6,3], семейство производит параллельный набор из 7 однородных мозаик евклидовой плоскости и их двойственных мозаик. Снова есть 3 чередования и полусимметричная версия.

Однородные шестиугольные / треугольные мозаики v т е
Симметрия : [6,3], (* 632)							[6,3] ⁺ (632)	[6,3 ⁺ ] (3 * 3)
{6,3}	т {6,3}	г {6,3}	т {3,6}	{3,6}	рр {6,3}	tr {6,3}	sr {6,3}	с {3,6}


6 3	3,12 2	(3,6) 2	6.6.6	3 6	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Униформа двойников

V6 3	Версия 3.12 2	В (3,6) 2	V6 3	V3 6	V3.4.6.4	V.4.6.12	V3 4 .6	V3 6

В гиперболической плоскости [7,3], семейство производит параллельный набор однородных мозаик и их двойственных мозаик. Есть только 1 чередование ( пренебрежение ), так как все порядки ветвления нечетные. Многие другие гиперболические семейства однородных мозаик можно увидеть на однородных мозаиках на гиперболической плоскости .

Равномерная семиугольная / треугольная мозаика v т е
Симметрия: [7,3], (* 732)							[7,3] ⁺ , (732)


{7,3}	т {7,3}	г {7,3}	т {3,7}	{3,7}	рр {7,3}	tr {7,3}	sr {7,3}
Униформа двойников


V7 3	V3.14.14	V3.7.3.7	V6.6.7	V3 7	V3.4.7.4	V4.6.14	V3.3.3.3.7

Аффинные группы Кокстера [ править ]

Семейства выпуклых равномерных евклидовых мозаик определяются аффинными группами Кокстера . Эти группы идентичны конечным группам с включением одного добавленного узла. В названиях букв они обозначаются одной и той же буквой со знаком «~» над буквой. Индекс относится к конечной группе, поэтому ранг является индексом плюс 1. ( Эрнст Witt символов для аффинных групп даны как и )

${\tilde {A}}_{n-1}$ : диаграммы этого типа являются циклами. (Также P _n )
${\tilde {C}}_{n-1}$ связана с семейством регулярных мозаик гиперкуба { $4, 3, ...., 4$ }. (Также R _n )
${\tilde {B}}_{n-1}$ связаны с C одним удаленным зеркалом. (Также S _n )
${\tilde {D}}_{n-1}$ связаны с C двумя удаленными зеркалами. (Также Q _n )
${\tilde {E}}_{6}$ , , . (Также T ₇ , T ₈ , T ₉ ) ${\tilde {E}}_{7}$ ${\tilde {E}}_{8}$
${\tilde {F}}_{4}$ образует обычную мозаику {3,4,3,3}. (Также U ₅ )
${\tilde {G}}_{2}$ образует 30-60-90 фундаментальных областей треугольника. (Также V ₃ )
${\tilde {I}}_{1}$ это два параллельных зеркала. (= = ) (Также W ₂ ) ${\tilde {A}}_{1}$ ${\tilde {C}}_{1}$

Составные группы также можно определить как ортогональные проекты. Наиболее частое использование , например , ${\tilde {A}}_{1}$ ${\tilde {A}}_{1}^{2}$ представляет квадратные или прямоугольные домены шахматной доски в евклидовой плоскости. И ${\tilde {A}}_{1}{\tilde {G}}_{2}$ представляет собой фундаментальные области треугольной призмы в трехмерном евклидовом пространстве.

Аффинные графы Кокстера до (от 2 до 10 узлов)
Классифицировать	${\tilde {A}}_{1+}$ (P ₂₊ )	${\tilde {B}}_{3+}$ (S ₄₊ )	${\tilde {C}}_{1+}$ (R ₂₊ )	${\tilde {D}}_{4+}$ (Q ₅₊ )	${\tilde {E}}_{n}$ (Т _{n + 1} ) / (U ₅ ) / (V ₃ ) ${\tilde {F}}_{4}$ ${\tilde {G}}_{2}$
2	${\tilde {A}}_{1}$ = [∞]		${\tilde {C}}_{1}$ = [∞]
3	${\tilde {A}}_{2}$ = [3 ^[3] ] *		${\tilde {C}}_{2}$ = [4,4] *		${\tilde {G}}_{2}$ = [6,3] *
4	${\tilde {A}}_{3}$ = [3 ^[4] ] *	${\tilde {B}}_{3}$ = [4,3 ^1,1 ] *	${\tilde {C}}_{3}$ = [4,3,4] *	${\tilde {D}}_{3}$ = [3 ^1,1 , 3 ⁻¹ , 3 ^1,1 ] знак равно ${\tilde {A}}_{3}$
5	${\tilde {A}}_{4}$ = [3 ^[5] ] *	${\tilde {B}}_{4}$ = [4,3,3 ^1,1 ] *	${\tilde {C}}_{4}$ = [4,3 ² , 4] *	${\tilde {D}}_{4}$ = [3 ^1,1,1,1 ] *	${\tilde {F}}_{4}$ = [3,4,3,3] *
6	${\tilde {A}}_{5}$ = [3 ^[6] ] *	${\tilde {B}}_{5}$ = [4,3 ² , 3 ^1,1 ] *	${\tilde {C}}_{5}$ = [4,3 ³ , 4] *	${\tilde {D}}_{5}$ = [3 ^1,1 , 3,3 ^1,1 ] *
7	${\tilde {A}}_{6}$ = [3 ^[7] ] *	${\tilde {B}}_{6}$ = [4,3 ³ , 3 ^1,1 ]	${\tilde {C}}_{6}$ = [4,3 ⁴ , 4]	${\tilde {D}}_{6}$ = [3 ^1,1 , 3 ² , 3 ^1,1 ]	${\tilde {E}}_{6}$ = [3 ^2,2,2 ]
8	${\tilde {A}}_{7}$ = [3 ^[8] ] *	${\tilde {B}}_{7}$ = [4,3 ⁴ , 3 ^1,1 ] *	${\tilde {C}}_{7}$ = [4,3 ⁵ , 4]	${\tilde {D}}_{7}$ = [3 ^1,1 , 3 ³ , 3 ^1,1 ] *	${\tilde {E}}_{7}$ = [3 ^3,3,1 ] *
9	${\tilde {A}}_{8}$ = [3 ^[9] ] *	${\tilde {B}}_{8}$ = [4,3 ⁵ , 3 ^1,1 ]	${\tilde {C}}_{8}$ = [4,3 ⁶ , 4]	${\tilde {D}}_{8}$ = [3 ^1,1 , 3 ⁴ , 3 ^1,1 ]	${\tilde {E}}_{8}$ = [3 ^5,2,1 ] *
10	${\tilde {A}}_{9}$ = [3 ^[10] ] *	${\tilde {B}}_{9}$ = [4,3 ⁶ , 3 ^1,1 ]	${\tilde {C}}_{9}$ = [4,3 ⁷ , 4]	${\tilde {D}}_{9}$ = [3 ^1,1 , 3 ⁵ , 3 ^1,1 ]
11	...	...	...	...

Гиперболические группы Кокстера [ править ]

Существует множество бесконечных гиперболических групп Кокстера . Гиперболические группы классифицируются как компактные или нет, причем компактные группы имеют ограниченные фундаментальные области. Компактные симплексные гиперболические группы ( симплексы Ланнера ) существуют с рангом от 3 до 5. Паракомпактные симплексные группы ( симплексы Кошуля ) существуют до ранга 10. Гиперкомпактные ( многогранники Винберга ) группы были исследованы, но не были полностью определены. В 2006 году Олкок доказал, что существует бесконечно много компактных многогранников Винберга размерности до 6 и бесконечно много многогранников Винберга конечного объема для размерности до 19 ^[4], поэтому полное перечисление невозможно. Все эти фундаментальные отражающие области, как симплексы, так и несимплексы, часто называютМногогранники Кокстера или иногда менее точно многогранники Кокстера .

Гиперболические группы в H ²[ править ]

Модель диска Пуанкаре фундаментальных треугольников области
Пример прямоугольных треугольников [p, q]
[3,7]	[3,8]	[3,9]	[3, ∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞, 4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞, ∞]
Пример общих треугольников [(p, q, r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3, ∞)]
[(3,4,4)]	[(3,6,6)]	[(3, ∞, ∞)]	[(6,6,6)]	[(∞, ∞, ∞)]

Двумерные гиперболические треугольные группы существуют как диаграммы Кокстера ранга 3, определяемые треугольником (pqr) для:

{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1.

Существует бесконечно много компактных треугольных гиперболических групп Кокстера, включая линейные и треугольные графы. Линейные графики существуют для прямоугольных треугольников (с r = 2). ^[5]

Компактные гиперболические группы Кокстера

Линейный

Циклический

∞ [p, q],

:
2 (p + q) <pq

...

...

...

∞ [(p, q, r)],

: p + q + r> 9

...

Паракомпактные группы Кокстера ранга 3 существуют как пределы компактных.

Линейные графики	Циклические графы
[p, ∞] [∞, ∞]	[(p, q, ∞)] [(p, ∞, ∞)] [(∞, ∞, ∞)]

Группа арифметических треугольников [ править ]

Группы гиперболических треугольников , которые также являются арифметическими группами, образуют конечное подмножество. Путем компьютерного поиска полный список был определен Кисао Такеучи в его статье 1977 года « Группы арифметических треугольников» . ^[6] Всего 85, компактных 76 и паракомпактных 9.

Правые треугольники (pq 2)

Общие треугольники (pqr)

Компактные группы: (76)

,

Паракомпактные прямоугольные треугольники: (4)

,

Общие треугольники: (39)

,

Паракомпактные общие треугольники: (5)

,

(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30)

(2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18),

(2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30)

(2 6 6), (2 6 8), (2 6 12)

(2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18)

(2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18)

(2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)

(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15)

(3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12)

(4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16)

(5 5 5), (5 5 10), (5 5 15), (5 10 10)

(6 6 6), (6 12 12), (6 24 24)

(7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15)

(3,3 ∞) (3 ∞ ∞)

(4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Гиперболические многоугольники Кокстера над треугольниками [ править ]

Фундаментальные области четырехугольных групп
Домены с идеальными вершинами
или же [∞, 3, ∞] [iπ / λ ₁ , 3, iπ / λ ₂ ] (* 3222)	или же [((3, ∞, 3)), ∞] [((3, iπ / λ ₁ , 3)), iπ / λ ₂ ] (* 3322)	или же [(3, ∞) ^[2] ] [(3, iπ / λ ₁ , 3, iπ / λ ₂ )] (* 3232)	или же [(4, ∞) ^[2] ] [(4, iπ / λ ₁ , 4, iπ / λ ₂ )] (* 4242)	(* 3333)
[iπ / λ ₁ , ∞, iπ / λ ₂ ] (* ∞222)	(* ∞∞22)	[(iπ / λ ₁ , ∞, iπ / λ ₂ , ∞)] (* 2∞2∞)	(* ∞∞∞∞)	(* 4444)

Другие гиперболические калейдоскопы H ² могут быть построены из многоугольников более высокого порядка. Как и группы треугольников, эти калейдоскопы можно идентифицировать по циклической последовательности порядков зеркального пересечения вокруг фундаментальной области, как (abcd ...), или, что эквивалентно, в орбифолдной нотации как * abcd .... Диаграммы Кокстера – Дынкина для этих полигональных калейдоскопов могут можно рассматривать как вырожденные (n-1) - симплексные фундаментальные области с циклическими ветвями порядка a, b, c ..., а оставшиеся n * (n-3) / 2 ветвей помечены как бесконечные (∞), представляющие непересекающиеся зеркала. Единственным негиперболическим примером является евклидова симметрия четырех зеркал в квадрате или прямоугольнике в виде, [∞, 2, ∞] (орбифолд * 2222). Другое представление ветвей для непересекающихся зеркал Винберга дает бесконечные ветви в виде пунктирных или штриховых линий, поэтому эту диаграмму можно представить как, с подавленными по периметру четырьмя ветвями порядка 2.

Например, четырехугольная область (abcd) будет иметь две ветви бесконечного порядка, соединяющие ультрапараллельные зеркала. Самый маленький гиперболический пример:, [∞, 3, ∞] или [iπ / λ ₁ , 3, iπ / λ ₂ ] (орбифолд * 3222), где (λ ₁ , λ ₂ ) - расстояние между ультрапараллельными зеркалами. Альтернативное выражение:, с подавленными по периметру тремя ветвями порядка 2. Аналогично (2 3 2 3) (орбифолд * 3232) можно представить в виде и (3 3 3 3), (orbifold * 3333) можно представить в виде полного графа .

Наивысшая четырехугольная область (∞ ∞ ∞ ∞) представляет собой бесконечный квадрат, представленный полным тетраэдрическим графом с 4 ветвями по периметру в виде идеальных вершин и двумя диагональными ветвями в виде бесконечности (показаны пунктирными линиями) для ультрапараллельных зеркал:.

Компактные (симплексные группы Ланнера) [ править ]

Компактные гиперболические группы называются группами Ланнера в честь Фольке Ланнера, который впервые изучил их в 1950 году. ^[7] Они существуют только как графы ранга 4 и 5. Косетер изучены линейных гиперболических групп Кокстера в его работе 1954 г. Регулярных Сот в гиперболическом пространстве , ^[8] , которые включены две рациональных решений в гиперболическом 4-пространстве : [5 / 2,5,3,3] = и [5,5 / 2,5,3] = .

Ранги 4–5 [ править ]

Фундаментальная область любой из двух бифуркационных групп, [5,3 ^1,1 ] и [5,3,3 ^1,1 ], вдвое больше, чем у соответствующей линейной группы, [5,3,4] и [5 , 3,3,4] соответственно. Имена букв даны Джонсоном как расширенные символы Витта . ^[9]

Компактные гиперболические группы Кокстера
Размер H ^d	Классифицировать	Общее количество	Линейный	Раздвоение	Циклический
H ³	4	9	3: ${\overline {BH}}_{3}$ = [4,3,5]: ${\overline {K}}_{3}$ = [5,3,5]: ${\overline {J}}_{3}$ = [3,5,3]:	${\overline {DH}}_{3}$ = [5,3 ^1,1 ]:	${\widehat {AB}}_{3}$ = [(3 ³ , 4)]: ${\widehat {AH}}_{3}$ = [(3 ³ , 5)]: ${\widehat {BB}}_{3}$ = [(3,4) ^[2] ]: ${\widehat {BH}}_{3}$ = [(3,4,3,5)]: ${\widehat {HH}}_{3}$ = [(3,5) ^[2] ]:
H ⁴	5	5	3: ${\overline {H}}_{4}$ = [3 ³ , 5]: ${\overline {BH}}_{4}$ = [4,3,3,5]: ${\overline {K}}_{4}$ = [5,3,3,5]:	${\overline {DH}}_{4}$ = [5,3,3 ^1,1 ]:	${\widehat {AF}}_{4}$ = [(3 ⁴ , 4)]:

Паракомпакт (симплексные группы Кошуля) [ править ]

Пример апейрогональной мозаики порядка 3 , {∞, 3} с одним зеленым апейрогоном и его описанным орициклом.

Паракомпактные (также называемые некомпактными) гиперболические группы Кокстера содержат аффинные подгруппы и имеют асимптотические симплексные фундаментальные области. Наивысшая паракомпактная гиперболическая группа Кокстера имеет ранг 10. Эти группы названы в честь французского математика Жана-Луи Кошуля . ^[10] Их также называют квазиланнеровскими группами, продолжающими компактные группы Ланнера. Полный список был составлен с помощью компьютерного поиска М. Чейном и опубликован в 1969 г. ^[11]

По Винбергу, все 72 компактных и паракомпактных симплекса, кроме восьми, являются арифметическими. Две из неарифметических групп компактны: и . Остальные шесть неарифметических групп все паракомпактны, с пятью трехмерными группами., , , , и , и одна 5-мерная группа .

Идеальные симплексы [ править ]

Идеальные фундаментальные области

, [(∞, ∞, ∞)] в модели диска Пуанкаре

Есть 5 гиперболических групп Кокстера, выражающих идеальные симплексы , графы, в которых удаление любого одного узла приводит к аффинной группе Кокстера. Таким образом, все вершины этого идеального симплекса находятся на бесконечности. ^[12]

Классифицировать	Идеальная группа	Аффинные подгруппы
3	[(∞, ∞, ∞)]	[∞]
4	[4 ^[4] ]	[4,4]
4	[3 ^[3,3] ]	[3 ^[3] ]
4	[(3,6) ^[2] ]	[3,6]
6	[(3,3,4) ^[2] ]	[4,3,3,4], [3,4,3,3]	,

Ранги 4–10 [ править ]

Бесконечные евклидовы ячейки, такие как гексагональная мозаика , правильно масштабируемая, сходятся к одной идеальной точке на бесконечности, как гексагональные мозаичные соты , {6,3,3}, как показано с этой единственной ячейкой в проекции модели диска Пуанкаре .

Всего существует 58 паракомпактных гиперболических групп Кокстера с рангов с 4 по 10. Все 58 сгруппированы ниже по пяти категориям. Буквенные символы даны Джонсоном как расширенные символы Витта с использованием PQRSTWUV из аффинных символов Витта и добавлением LMNOXYZ. Этим гиперболическим группам для циклохимических схем дается верхняя черта или шляпа. Кронштейн обозначение от Кокстера является линеаризованным представлением группы Кокстера.

Гиперболические паракомпактные группы
Классифицировать	Общее количество	Группы
4	23	${\widehat {BR}}_{3}$ = [(3,3,4,4)]: ${\widehat {CR}}_{3}$ = [(3,4 ³ )]: ${\widehat {RR}}_{3}$ = [4 ^[4] ]: ${\widehat {AV}}_{3}$ = [(3 ³ , 6)]: ${\widehat {BV}}_{3}$ = [(3,4,3,6)]: ${\widehat {HV}}_{3}$ = [(3,5,3,6)]: ${\widehat {VV}}_{3}$ = [(3,6) ^[2] ]:	${\overline {P}}_{3}$ = [3,3 ^[3] ]: ${\overline {BP}}_{3}$ = [4,3 ^[3] ]: ${\overline {HP}}_{3}$ = [5,3 ^[3] ]: ${\overline {VP}}_{3}$ = [6,3 ^[3] ]: ${\overline {DV}}_{3}$ = [6,3 ^1,1 ]: ${\overline {O}}_{3}$ = [3,4 ^1,1 ]: ${\overline {M}}_{3}$ = [4 ^1,1,1 ]:	${\overline {R}}_{3}$ = [3,4,4]: ${\overline {N}}_{3}$ = [4 ³ ]: ${\overline {V}}_{3}$ = [3,3,6]: ${\overline {BV}}_{3}$ = [4,3,6]: ${\overline {HV}}_{3}$ = [5,3,6]: ${\overline {Y}}_{3}$ = [3,6,3]: ${\overline {Z}}_{3}$ = [6,3,6]:	${\overline {DP}}_{3}$ = [3 ^{[] x []} ]: ${\overline {PP}}_{3}$ = [3 ^[3,3] ]:
5	9	${\overline {P}}_{4}$ = [3,3 ^[4] ]: ${\overline {BP}}_{4}$ = [4,3 ^[4] ]: ${\widehat {FR}}_{4}$ = [(3 ² , 4,3,4)]: ${\overline {DP}}_{4}$ = [3 ^{[3] x []} ]:	${\overline {N}}_{4}$ = [4,3, ((4,2,3))]: ${\overline {O}}_{4}$ = [3,4,3 ^1,1 ]: ${\overline {S}}_{4}$ = [4,3 ^2,1 ]:	${\overline {R}}_{4}$ = [(3,4) ² ]:	${\overline {M}}_{4}$ = [4,3 ^1,1,1 ]:
6	12	${\overline {P}}_{5}$ = [3,3 ^[5] ]: ${\widehat {AU}}_{5}$ = [(3 ⁵ , 4)]: ${\widehat {AR}}_{5}$ = [(3,3,4) ^[2] ]:	${\overline {S}}_{5}$ = [4,3,3 ^2,1 ]: ${\overline {O}}_{5}$ = [3,4,3 ^1,1 ]: ${\overline {N}}_{5}$ = [3, (3,4) ^1,1 ]:	${\overline {U}}_{5}$ = [3 ³ , 4,3]: ${\overline {X}}_{5}$ = [3,3,4,3,3]: ${\overline {R}}_{5}$ = [3,4,3,3,4]:	${\overline {Q}}_{5}$ = [3 ^2,1,1,1 ]: ${\overline {M}}_{5}$ = [4,3,3 ^1,1,1 ]: ${\overline {L}}_{5}$ = [3 ^1,1,1,1,1 ]:
7	3	${\overline {P}}_{6}$ = [3,3 ^[6] ]:	${\overline {Q}}_{6}$ = [3 ^1,1 , 3,3 ^2,1 ]:	${\overline {S}}_{6}$ = [4,3 ² , 3 ^2,1 ]:
8	4	${\overline {P}}_{7}$ = [3,3 ^[7] ]:	${\overline {Q}}_{7}$ = [3 ^1,1 , 3 ² , 3 ^2,1 ]:	${\overline {S}}_{7}$ = [4,3 ³ , 3 ^2,1 ]:	${\overline {T}}_{7}$ = [3 ^3,2,2 ]:
9	4	${\overline {P}}_{8}$ = [3,3 ^[8] ]:	${\overline {Q}}_{8}$ = [3 ^1,1 , 3 ³ , 3 ^2,1 ]:	${\overline {S}}_{8}$ = [4,3 ⁴ , 3 ^2,1 ]:	${\overline {T}}_{8}$ = [3 ^4,3,1 ]:
10	4	${\overline {P}}_{9}$ = [3,3 ^[9] ]:	${\overline {Q}}_{9}$ = [3 ^1,1 , 3 ⁴ , 3 ^2,1 ]:	${\overline {S}}_{9}$ = [4,3 ⁵ , 3 ^2,1 ]:	${\overline {T}}_{9}$ = [3 ^6,2,1 ]:

Подгрупповые отношения паракомпактных гиперболических групп [ править ]

Эти деревья представляют собой отношения подгрупп паракомпактных гиперболических групп. Индексы подгрупп на каждом подключении выделены красным цветом. ^[13] Подгруппы индекса 2 представляют собой зеркальное удаление и фундаментальное удвоение домена. Другие могут быть выведены с помощью соизмеримости (целочисленного отношения объемов) для тетраэдрических доменов.

Деревья подгрупп
H ³
H ⁴
H ⁵

Гиперкомпактные группы Кокстера (многогранники Винберга) [ править ]

Точно так же, как гиперболическая плоскость H ² имеет нетреугольные многоугольные области, существуют также многомерные отражающие гиперболические области. Эти несимплексные области можно рассматривать как вырожденные симплексы с непересекающимися зеркалами, заданными бесконечным порядком, или на диаграмме Кокстера такие ветви обозначены пунктирными или штриховыми линиями. Эти несимплексные области называются многогранниками Винберга в честь Эрнеста Винберга за его алгоритм Винберга для поиска несимплексной фундаментальной области гиперболической группы отражений. Геометрически эти фундаментальные области можно классифицировать как четырехугольные пирамиды , призмы или другие многогранники.с краями как пересечение двух зеркал, имеющих двугранные углы как π / n для n = 2,3,4 ...

В симплексной области имеется n +1 зеркал для n-мерного пространства. В не симплексных доменах имеется более n +1 зеркал. Список конечен, но не полностью известен. Вместо этого частичные списки были пронумерованы как n + k зеркал для k как 2, 3 и 4.

Гиперкомпактные группы Кокстера в трехмерном пространстве или выше отличаются от двухмерных групп в одном существенном отношении. Два гиперболических n-угольника с одинаковыми углами в одном и том же циклическом порядке могут иметь разные длины ребер и в общем случае не совпадают . В отличие от многогранников Винберга в трех измерениях или выше полностью определяются двугранными углами. Этот факт основан на теореме о жесткости Мостова , согласно которой две изоморфные группы, порожденные отражениями в H ⁿ для n> = 3, определяют конгруэнтные фундаментальные области (многогранники Винберга).

Многогранники Винберга ранга n + 2 для n-мерного пространства [ править ]

Полный список компактных гиперболических многогранников Винберга с зеркалами ранга n + 2 для n-мерности был перечислен Ф. Эссельманном в 1996 г. ^[14] Частичный список был опубликован в 1974 г. И. М. Каплинской. ^[15]

Полный список паракомпактных решений был опубликован П. Тумаркиным в 2003 г. с размерами от 3 до 17. ^[16]

Самая маленькая паракомпактная форма в H ³ может быть представлена, или [∞, 3,3, ∞], который может быть построен путем зеркального удаления паракомпактной гиперболической группы [3,4,4] как [3,4,1 ⁺ , 4]. Двойная основная область превращается из тетраэдра в четырехугольную пирамиду. Другие пирамиды включают [4,4,1 ⁺ , 4] = [∞, 4,4, ∞], знак равно . Удаление зеркала из некоторых циклических гиперболических графов Кокстера превращается в графы-бабочки: [(3,3,4,1 ⁺ , 4)] = [((3, ∞, 3)), ((3, ∞, 3 ))] или же, [(3,4,4,1 ⁺ , 4)] = [((4, ∞, 3)), ((3, ∞, 4))] или, [(4,4,4,1 ⁺ , 4)] = [((4, ∞, 4)), ((4, ∞, 4))] или.

Другие допустимые паракомпактные графы с фундаментальными областями четырехугольной пирамиды включают:

Измерение	Классифицировать	Графики
H ³	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

Другая подгруппа [1 ⁺ , 4 ^1,1,1 ] = [∞, 4,1 ⁺ , 4, ∞] = [∞ ^[6] ]. знак равно знак равно .^[17]

Многогранники Винберга ранга n + 3 для n-мерного пространства [ править ]

Существует конечное число вырожденных фундаментальных симплексов, которые могут существовать вплоть до 8-мерных. Полный список компактных многогранников Винберга с зеркалами ранга n + 3 для n-мерности был перечислен П. Тумаркиным в 2004 году. Эти группы помечены пунктирными / ломаными линиями для ультрапараллельных ветвей. Полный список некомпактных многогранников Винберга с зеркалами ранга n + 3 и с одной непростой вершиной для n-мерности перечислил Майк Робертс. ^[18]

Для 4-8 измерений группы Кокстера с 7 по 11 ранги считаются как 44, 16, 3, 1 и 1 соответственно. ^[19] Наивысшее было обнаружено Бугаенко в 1984 г. в размерности 8, ранг 11: ^[20]

Размеры	Классифицировать	Случаи	Графики
H ⁴	7	44 год	...
H ⁵	8	16	..
H ⁶	9	3
H ⁷	10	1
H ⁸	11	1

Многогранники Винберга ранга n + 4 для n-мерного пространства [ править ]

Существует конечное число вырожденных фундаментальных симплексов, которые могут существовать вплоть до 8-мерных. Компактные многогранники Винберга с зеркалами ранга n + 4 для n-мерности были исследованы А. Феликсоном и П. Тумаркиным в 2005 г. ^[21]

Лоренцевы группы [ править ]

Регулярные соты с лоренцевыми группами
{3,3,7} просмотр вне модели шара Пуанкаре	{7,3,3} просмотр вне модели шара Пуанкаре

Это показывает лоренцевы группы 5-го ранга, упорядоченные как подгруппы из [6,3,3,3] и [6,3,6,3]. Высокосимметричная группа

, [3 ^[3,3,3] ] - подгруппа индекса 120 в [6,3,3,3].

Лоренцевы группы для симплексных областей могут быть определены как графы за пределами паракомпактных гиперболических форм. Их иногда называют суперидеальными симплексами, и они также связаны с лоренцевой геометрией , названной в честь Хендрика Лоренца в области специальной и общей теории относительности пространства-времени, содержащей одну (или несколько) подобных времени компоненту размерности, чьи собственные точечные произведения отрицательны. . ^[9] Дэнни Калегари называет эти выпуклые кокомпактные группы Кокстера в n-мерном гиперболическом пространстве. ^[22]^[23]

В статье Джорджа Максвелла 1982 года « Сферические упаковки и гиперболические группы отражений» перечислен конечный список лоренцевых рангов от 5 до 11. Он называет их уровнем 2 , что означает, что удаление любой перестановки двух узлов оставляет конечный или евклидов граф. Его перечисление является полным, но не перечисляет графы, которые являются подгруппой другой. Все ветвящиеся группы Кокстера высокого порядка ранга-4 являются лоренцевыми и заканчиваются в пределе полной графической 3- симплексной диаграммой Кокстера-Дынкина с 6 ветвями бесконечного порядка, которые могут быть выражены как [∞ ^[3,3] ]. Ранги 5-11 имеют конечное число групп 186, 66, 36, 13, 10, 8 и 4 лоренцевы группы соответственно. ^[24]Статья Х. Чена и Ж.-П. Лаббе, группы Лоренца-Кокстера и упаковки шариков Бойда-Максвелла пересчитали и опубликовали полный список. ^[25]

Для высших рангов 8-11 полные списки:

Лоренцевы группы Кокстера
Классифицировать	Общее количество	Группы
4	∞	[3,3,7] ... [∞, ∞, ∞]: ... [4,3 ^[3] ] ... [∞, ∞ ^[3] ]:... [5,4 ^1,1 ] ... [∞ ^1,1,1 ]:... ... [(5,4,3,3)] ... [∞ ^[4] ]: ...... ... [4 ^{[] × []} ] ... [∞ ^{[] × []} ]: ... ... [4 ^[3,3] ] ... [∞ ^[3,3] ]
5	186	... [3 ^[3,3,3] ]:...
6	66
7	36	[3 ^1,1,1,1,1,1 ]:...
8	13	[3,3,3 ^[6] ]: [3,3 ^[6] , 3]: [3,3 ^{[2 + 4]} , 3]: [3,3 ^{[1 + 5]} , 3]: [3 ^{[] e × [3]} ]:	[4,3,3,3 ^3,1 ]: [3 ^1,1 , 3,3 ^3,1 ]: [3, (3,3,4) ^1,1 ]: [3 ^2,1 , 3,3 ^2,1 ]:		[4,3,3,3 ^2,2 ]: [3 ^1,1 , 3,3 ^2,2 ]:
9	10	[3,3 ^{[3 + 4]} , 3]: [3,3 ^[9] ]: [3,3 ^{[2 + 5]} , 3]:	[3 ^2,1 , 3 ² , 3 ^2,1 ]:	[3 ^3,1 , 3 ³ , 4]: [3 ^3,1 , 3,3,3 ^1,1 ]:	[3 ^3,3,2 ]: [3 ^2,2,4 ]: [3 ^2,2 , 3 ³ , 4]: [3 ^2,2 , 3,3,3 ^1,1 ]:
10	8	[3,3 ^[8] , 3]: [3,3 ^{[3 + 5]} , 3]: [3,3 ^[9] ]:	[3 ^2,1 , 3 ³ , 3 ^2,1 ]:	[3 ^5,3,1 ]: [3 ^3,1 , 3 ⁴ , 4]: [3 ^3,1 , 3 ³ , 3 ^1,1 ]:	[3 ^4,4,1 ]:
11	4		[3 ^2,1 , 3 ⁴ , 3 ^2,1 ]:	[3 ^2,1 , 3 ⁶ , 4]: [3 ^2,1 , 3 ⁵ , 3 ^1,1 ]:	[3 ^7,2,1 ]:

Очень расширенные диаграммы Кокстера [ править ]

Одно использование включает очень расширенное определение из прямого использования диаграммы Дынкина, которое рассматривает аффинные группы как расширенные , гиперболические группы сверхрасширенными , а третий узел как очень расширенные простые группы. Эти расширения обычно обозначаются показателем степени 1,2 или 3+ для количества расширенных узлов. Эту расширяющуюся серию можно продолжить назад, последовательно удаляя узлы из одной и той же позиции в графе, хотя процесс останавливается после удаления узла ветвления. Е 8 расширенная семья является наиболее часто показан пример расширения в обратном направлении от Е ₃ и вперед Е ₁₁.

Процесс расширения может определять ограниченную серию графов Кокстера, которые прогрессируют от конечного к аффинному и от гиперболического к лоренцеву. Определитель матриц Картана определяет, где ряд изменяется от конечного (положительного) до аффинного (ноль) до гиперболического (отрицательного) и заканчивается лоренцевой группой, содержащей по крайней мере одну гиперболическую подгруппу. ^[26] Некристалографические группы H _n образуют расширенную серию, в которой H ₄ расширяется как компактная гиперболическая группа и сверх-расширяется до лоренцевой группы.

Определители матрицы Шлефли по рангу следующие: ^[27]

det (A ₁ⁿ = [2 ^n-1 ]) = 2 ⁿ (Конечное для всех n)
det (A _n = [3 ^n-1 ]) = n + 1 (Конечное для всех n)
det (B _n = [4,3 ^n-2 ]) = 2 (Конечное для всех n)
det (D _n = [3 ^n-3,1,1 ]) = 4 (Конечное для всех n)

Детерминанты матрицы Шлефли в исключительных рядах:

det ( E n = [3 ^n-3,2,1 ]) = 9-n (Конечное для E ₃ (= A ₂ A ₁ ), E ₄ (= A ₄ ), E ₅ (= D ₅ ), E 6 , E 7 и E 8 , аффинные в E 9 ( ), гиперболические в E ₁₀ ) ${\tilde {E}}_{8}$
det ([3 ^n-4,3,1 ]) = 2 (8-n) (Конечное для n = от 4 до 7, affine ( ) и гиперболическое при n = 8.) ${\tilde {E}}_{7}$
det ([3 ^n-4,2,2 ]) = 3 (7-n) (Конечное для n = от 4 до 6, affine ( ) и гиперболическое при n = 7.) ${\tilde {E}}_{6}$
det (F _n = [3,4,3 ^n-3 ]) = 5-n (Конечное для F ₃ (= B ₃ ) до F 4 , аффинное в F 5 ( ), гиперболическое в F ₆ ) ${\tilde {F}}_{4}$
det (G _n = [6,3 ^n-2 ]) = 3-n (конечный для G 2 , аффинный в G ₃ ( ), гиперболический в G ₄ ) ${\tilde {G}}_{2}$

Меньшая расширенная серия
Конечный	$A_{2}$	$C_{2}$	G 2 {\displaystyle G_{2}}	$A_{3}$	$B_{3}$	$C_{3}$	$H_{4}$
Ранг n	[3 ^[3] , 3 ^n-3 ]	[4,4,3 ^п-3 ]	G _n = [6,3 ^n-2 ]	[3 ^[4] , 3 ^n-4 ]	[4,3 ^{1, n-3} ]	[4,3,4,3 ^п-4 ]	H _n = [5,3 ^n-2 ]
2	[3] A ₂	[4] C ₂	[6] G ₂		[2] A ₁²	[4] C ₂	[5] H ₂
3	[3 ^[3] ] A ₂⁺ = ${\tilde {A}}_{2}$	[4,4] C ₂⁺ = ${\tilde {C}}_{2}$	[6,3] G ₂⁺ = ${\tilde {G}}_{2}$	[3,3] = A ₃	[4,3] B ₃	[4,3] C ₃	[5,3] H ₃
4	[3 ^[3] , 3] A ₂⁺⁺ = ${\overline {P}}_{3}$	[4,4,3] C ₂⁺⁺ = ${\overline {R}}_{3}$	[6,3,3] G ₂⁺⁺ = ${\overline {V}}_{3}$	[3 ^[4] ] A ₃⁺ = ${\tilde {A}}_{3}$	[4,3 ^1,1 ] B ₃⁺ = ${\tilde {B}}_{3}$	[4,3,4] C ₃⁺ = ${\tilde {C}}_{3}$	[5,3,3] H ₄
5	[3 ^[3] , 3,3] A ₂⁺⁺⁺	[4,4,3,3] C ₂⁺⁺⁺	[6,3,3,3] G ₂⁺⁺⁺	[3 ^[4] , 3] A ₃⁺⁺ = ${\overline {P}}_{4}$	[4,3 ^2,1 ] B ₃⁺⁺ = ${\overline {S}}_{4}$	[4,3,4,3] C ₃⁺⁺ = ${\overline {R}}_{4}$	[5,3 ³ ] H ₅ = ${\overline {H}}_{4}$
6				[3 ^[4] , 3,3] А ₃⁺⁺⁺	[4,3 ^3,1 ] В ₃⁺⁺⁺	[4,3,4,3,3] C ₃⁺⁺⁺	[5,3 ⁴ ] H ₆
Дет (М _п )	3 (3- н )	2 (3- н )	3- п	4 (4- н )	2 (4- н )

Средняя расширенная серия
Конечный	$A_{4}$	$B_{4}$	$C_{4}$	$D_{4}$	F 4 {\displaystyle F_{4}}	$A_{5}$	$B_{5}$	$D_{5}$
Ранг n	[3 ^[5] , 3 ^n-5 ]	[4,3,3 ^п-4,1 ]	[4,3,3,4,3 ^п-5 ]	[3 ^п-4,1,1,1 ]	[3,4,3 ^п-3 ]	[3 ^[6] , 3 ^n-6 ]	[4,3,3,3 ^п-5,1 ]	[3 ^1,1 , 3,3 ^n-5,1 ]
3		[4,3 ^−1,1 ] B ₂ A ₁	[4,3] B ₃	[3 ^−1,1,1,1 ] A ₁³	[3,4] В ₃		[4,3,3] C ₃
4	[3 ³ ] A ₄	[4,3,3] В ₄	[4,3,3] C ₄	[3 ^0,1,1,1 ] D ₄	[3,4,3] Ж ₄		[4,3,3,3 ^−1,1 ] B ₃ A ₁	[3 ^1,1 , 3,3 ^−1,1 ] A ₃ A ₁
5	[3 ^[5] ] A ₄⁺ = ${\tilde {A}}_{4}$	[4,3,3 ^1,1 ] B ₄⁺ = ${\tilde {B}}_{4}$	[4,3,3,4] C ₄⁺ = ${\tilde {C}}_{4}$	[3 ^1,1,1,1 ] D ₄⁺ = ${\tilde {D}}_{4}$	[3,4,3,3] F ₄⁺ = ${\tilde {F}}_{4}$	[3 ⁴ ] A ₅	[4,3,3,3,3] В ₅	[3 ^1,1 , 3,3] D ₅
6	[3 ^[5] , 3] A ₄⁺⁺ = ${\overline {P}}_{5}$	[4,3,3 ^2,1 ] B ₄⁺⁺ = ${\overline {S}}_{5}$	[4,3,3,4,3] C ₄⁺⁺ = ${\overline {R}}_{5}$	[3 ^2,1,1,1 ] D ₄⁺⁺ = ${\overline {Q}}_{5}$	[3,4,3 ³ ] F ₄⁺⁺ = ${\overline {U}}_{5}$	[3 ^[6] ] A ₅⁺ = ${\tilde {A}}_{5}$	[4,3,3,3 ^1,1 ] B ₅⁺ = ${\tilde {B}}_{5}$	[3 ^1,1 , 3,3 ^1,1 ] D ₅⁺ = ${\tilde {D}}_{5}$
7	[3 ^[5] , 3,3] A ₄⁺⁺⁺	[4,3,3 ^3,1 ] В ₄⁺⁺⁺	[4,3,3,4,3,3] C ₄⁺⁺⁺	[3 ^3,1,1,1 ] D ₄⁺⁺⁺	[3,4,3 ⁴ ] F ₄⁺⁺⁺	[3 ^[6] , 3] A ₅⁺⁺ = ${\overline {P}}_{6}$	[4,3,3,3 ^2,1 ] B ₅⁺⁺ = ${\overline {S}}_{6}$	[3 ^1,1 , 3,3 ^2,1 ] D ₅⁺⁺ = ${\overline {Q}}_{6}$
8						[3 ^[6] , 3,3] A ₅⁺⁺⁺	[4,3,3,3 ^3,1 ] В ₅⁺⁺⁺	[3 ^1,1 , 3,3 ^3,1 ] D ₅⁺⁺⁺
Дет (М _п )	5 (5- н )	2 (5- н )		4 (5- н )	5- н	6 (6- н )	4 (6- н )

Некоторые высшие расширенные серии
Конечный	$A_{6}$	$B_{6}$	$D_{6}$	$E_{6}$	$A_{7}$	$B_{7}$	$D_{7}$	$E_{7}$	E 8 {\displaystyle E_{8}}
Ранг n	[3 ^[7] , 3 ^n-7 ]	[4,3 ³ , 3 ^n-6,1 ]	[3 ^1,1 , 3,3,3 ^п-6,1 ]	[3 ^п-5,2,2 ]	[3 ^[8] , 3 ^n-8 ]	[4,3 ⁴ , 3 ^n-7,1 ]	[3 ^1,1 , 3,3,3,3 ^п-7,1 ]	[3 ^п-5,3,1 ]	E _n = [3 ^n-4,2,1 ]
3									[3 ^−1,2,1 ] E ₃ = A ₂ A ₁
4				[3 ^−1,2,2 ] А ₂²				[3 ^−1,3,1 ] A ₃ A ₁	[3 ^0,2,1 ] E ₄ = A ₄
5		[4,3,3,3,3 ^−1,1 ] B ₄ A ₁	[3 ^1,1 , 3,3,3 ^−1,1 ] D ₄ A ₁	[3 ^0,2,2 ] А ₅				[3 ^0,3,1 ] A ₅	[3 ^1,2,1 ] E ₅ = D ₅
6	[3 ⁵ ] A ₆	[4,3 ⁴ ] В ₆	[3 ^1,1 , 3,3,3] D ₆	[3 ^1,2,2 ] E ₆		[4,3,3,3,3,3 ^−1,1 ] B ₅ A ₁	[3 ^1,1 , 3,3,3,3 ^−1,1 ] D ₅ A ₁	[3 ^1,3,1 ] D ₆	[3 ^2,2,1 ] E ₆ *
7	[3 ^[7] ] A ₆⁺ = ${\tilde {A}}_{6}$	[4,3 ³ , 3 ^1,1 ] B ₆⁺ = ${\tilde {B}}_{6}$	[3 ^1,1 , 3,3,3 ^1,1 ] D ₆⁺ = ${\tilde {D}}_{6}$	[3 ^2,2,2 ] E ₆⁺ = ${\tilde {E}}_{6}$	[3 ⁶ ] A ₇	[4,3 ⁵ ] В ₇	[3 ^1,1 , 3,3,3,3 ^0,1 ] D ₇	[3 ^2,3,1 ] E ₇ *	[3 ^3,2,1 ] E ₇ *
8	[3 ^[7] , 3] A ₆⁺⁺ = ${\overline {P}}_{7}$	[4,3 ³ , 3 ^2,1 ] B ₆⁺⁺ = ${\overline {S}}_{7}$	[3 ^1,1 , 3,3,3 ^2,1 ] D ₆⁺⁺ = ${\overline {Q}}_{7}$	[3 ^3,2,2 ] E ₆⁺⁺ = ${\overline {T}}_{7}$	[3 ^[8] ] A ₇⁺ = * ${\tilde {A}}_{7}$	[4,3 ⁴ , 3 ^1,1 ] B ₇⁺ = * ${\tilde {B}}_{7}$	[3 ^1,1 , 3,3,3,3 ^1,1 ] D ₇⁺ = * ${\tilde {D}}_{7}$	[3 ^3,3,1 ] E ₇⁺ = * ${\tilde {E}}_{7}$	[3 ^4,2,1 ] E ₈ *
9	[3 ^[7] , 3,3] A ₆⁺⁺⁺	[4,3 ³ , 3 ^3,1 ] B ₆⁺⁺⁺	[3 ^1,1 , 3,3,3 ^3,1 ] D ₆⁺⁺⁺	[3 ^4,2,2 ] E ₆⁺⁺⁺	[3 ^[8] , 3] A ₇⁺⁺ = * ${\overline {P}}_{8}$	[4,3 ⁴ , 3 ^2,1 ] B ₇⁺⁺ = * ${\overline {S}}_{8}$	[3 ^1,1 , 3,3,3,3 ^2,1 ] D ₇⁺⁺ = * ${\overline {Q}}_{8}$	[3 ^4,3,1 ] E ₇⁺⁺ = * ${\overline {T}}_{8}$	[3 ^5,2,1 ] E ₉ = E ₈⁺ = * ${\tilde {E}}_{8}$
10					[3 ^[8] , 3,3] A ₇⁺⁺⁺ *	[4,3 ⁴ , 3 ^3,1 ] B ₇⁺⁺⁺ *	[3 ^1,1 , 3,3,3,3 ^3,1 ] D ₇⁺⁺⁺ *	[3 ^5,3,1 ] E ₇⁺⁺⁺ *	[3 ^6,2,1 ] E ₁₀ = E ₈⁺⁺ = * ${\overline {T}}_{9}$
11									[3 ^7,2,1 ] E ₁₁ = E ₈⁺⁺⁺ *
Дет (М _п )	7 (7- н )	2 (7- н )	4 (7- н )	3 (7- н )	8 (8- н )	2 (8- н )	4 (8- н )	2 (8- н )	9- н

Геометрическое складывание [ править ]

Конечные и аффинные складки ^[28]
ф _А : А _Г -> А _{Г '} для конечных типов
Γ	Γ '	Описание складывания	Диаграммы Кокстера – Дынкина
I ₂ ( ч )	Γ (h)	Двугранная складка
B _n	А _2н	(Я, с _п )
B _n	Д _{п + 1} , А _2n-1	(A ₃ , + / - ε)
П ₄	E ₆	(A ₃ , ± ε)
H ₄	E ₈	(A ₄ , ± ε)
H ₃	D ₆
H ₂	А ₄
G ₂	А ₅	(A ₅ , ± ε)
G ₂	D ₄	(D ₄ , ± ε)
φ: A _Γ⁺ -> A _{Γ '}⁺ для аффинных типов
${\tilde {A}}_{n-1}$	${\tilde {A}}_{kn-1}$	Локально тривиально
${\tilde {B}}_{n}$	${\tilde {D}}_{2n+1}$	(Я, с _п )
${\tilde {B}}_{n}$	${\tilde {D}}_{n+1}$ , ${\tilde {D}}_{2n}$	(A ₃ , ± ε)
${\tilde {C}}_{n}$	${\tilde {B}}_{n+1}$ , ${\tilde {C}}_{2n}$	(A ₃ , ± ε)
${\tilde {C}}_{n}$	${\tilde {C}}_{2n+1}$	(Я, с _п )
${\tilde {C}}_{n}$	${\tilde {A}}_{2n+1}$	(I, s _n ) & (I, s ₀ )
	${\tilde {A}}_{2n}$	(A ₃ , ε) & (I, s ₀ )
	${\tilde {A}}_{2n-1}$	(A ₃ , ε) и (A ₃ , ε ')
${\tilde {C}}_{n}$	${\tilde {D}}_{n+2}$	(A ₃ , -ε) и (A ₃ , -ε ')
${\tilde {C}}_{2}$	${\tilde {D}}_{5}$	(I, s ₁ )
${\tilde {F}}_{4}$	${\tilde {E}}_{6}$ , ${\tilde {E}}_{7}$	(A ₃ , ± ε)
${\tilde {G}}_{2}$	${\tilde {D}}_{6}$ , ${\tilde {E}}_{7}$	(A ₅ , ± ε)
	${\tilde {B}}_{3}$ , ${\tilde {F}}_{4}$	(B ₃ , ± ε)
	${\tilde {D}}_{4}$ , ${\tilde {E}}_{6}$	(D ₄ , ± ε)

Диаграмма Кокстера – Дынкина (конечная, аффинная или гиперболическая) (с простыми шнурами), имеющая симметрию (удовлетворяющую одному условию, приведенному ниже), может быть факторно дифференцирована по симметрии, давая новую, как правило, диаграмму с множеством шнуров, с процессом, называемым " складной ". ^[29]^[30]

Например, при сворачивании D ₄ в G ₂ край в G ₂ указывает от класса 3 внешних узлов (валентность 1) к классу центрального узла (валентность 3). И E ₈ складывается в 2 копии H ₄ , вторая копия масштабируется на τ . ^[31]

Геометрически это соответствует ортогональных проекций на однородных многогранников и мозаик. Примечательно, что любую конечную диаграмму Кокстера – Дынкина с простыми шнурами можно свернуть до I ₂ ( h ), где h - число Кокстера , которое геометрически соответствует проекции на плоскость Кокстера .

Несколько гиперболических складок

Сложные размышления [ править ]

Диаграммы Кокстера – Дынкина были расширены на комплексное пространство , C ^n, где узлы являются унитарными отражениями с периодом больше 2. Узлы помечаются индексом, который, если он подавлен, предполагается равным 2 для обычного реального отражения. Кокстер записывает комплексную группу p [q] r как диаграмму. ^[32]

Одномерный регулярный комплексный многогранник в представлен в виде $\mathbb {C} ^{1}$ , имеющий p вершин. Его реальное представление - правильный многоугольник { p }. Его симметрия _p [] или, заказ p . Унитарный оператор генераторрассматривается как поворот на 2π / p радиан против часовой стрелки , а $\mathbb {R} ^{2}$ край создается последовательным применением одного унитарного отражения. Генератор унитарного отражения для 1-многогранника с p вершинами равен $e$ $2π$ $i$ $/$ $p$ $= cos (2π /$ $p$ $) +$ $i$ $sin (2π /$ $p$ $)$ . Когда p = 2, генератор e ^πⁱ = –1, то же самое, что и точечное отражение в реальной плоскости.

В более высоком многограннике _p {} илипредставляет собой элемент p- кромки с 2-гранью, {} или, представляющий собой обычное реальное ребро между двумя вершинами.

Правильные комплексные 1-многогранники
Сложные 1-многогранники, , представленные на плоскости Аргана в виде правильных многоугольников для p = 2, 3, 4, 5 и 6 с черными вершинами. Центроид p вершин показан красным цветом. Стороны многоугольников представляют одно приложение генератора симметрии, сопоставляя каждую вершину со следующей копией против часовой стрелки. Эти полигональные стороны не краевые элементы многогранника, как комплекс 1-многогранник может не иметь края (часто это сложный край) и содержит только элементы вершин.

12 неприводимых групп Шепарда с их отношениями индексов подгрупп. ^[33] Подгруппы индекса 2 связаны удалением реального отражения:
_p [2 q ] ₂ -> _p [ q ] _p , index 2.
_p [4] _q -> _p [ q ] _p , index q .

_p [4]₂ подгруппы: p = 2,3,4 ...
_p [4]₂ -> [ p ], индекс p
_p [4]₂ ->_p [] ×_p [], индекс 2

Aa регулярные сложные многоугольники в , имеет вид _р { д } _г или Кокстер диаграмму $\mathbb {C} ^{2}$ . Группа симметрии правильного сложного многоугольникане называется группой Кокстера , а скорее группой Шепарда , типом комплексной группы отражения . Порядок _p [ q ] _r равен . ^[34] $8/q\cdot (1/p+2/q+1/r-1)^{-2}$

Группы Шепарда 2-го ранга: ₂ [ q ] ₂ , _p [4] ₂ , ₃ [3] ₃ , ₃ [6] ₂ , ₃ [4] ₃ , ₄ [3] ₄ , ₃ [8] ₂ , _{4 ».} [6] ₂ , ₄ [4] ₃ , ₃ [5] ₃ , ₅ [3] ₅ , ₃ [10] ₂ , ₅ [6] ₂ и ₅[4] ₃ или, , , , , , , , , , , , , порядка 2 q , 2 p ² , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 и 1800 соответственно.

Группа симметрии _{p ₁} [ q ] _{p ₂} представлена двумя образующими R ₁ , R ₂ , где: R ₁^{p ₁} = R ₂^{p ₂} = I. Если q четно, (R ₂ R ₁ ) ^{q / 2} = (R ₁ R ₂ ) ^{д / 2} . Если q нечетное, (R ₂ R ₁ ) ^{(q-1) / 2} R ₂ = (R ₁ R ₂ ) ^{( q-1) / 2} R ₁ . Когда q нечетное, p ₁ = p ₂ .

группа $\mathbb {C} ^{3}$ или [1 1 1] ^p определяется 3 унитарными отражениями периода 2 {R ₁ , R ₂ , R ₃ }: R ₁² = R ₁² = R ₃² = (R ₁ R ₂ ) ³ = (R ₂ R ₃ ) ³ = (R ₃ R ₁ ) ³ = (R ₁ R ₂ R ₃ R ₁ ) ^p = 1. Период p можно рассматривать как двойное вращение в реальном времени . $\mathbb {R} ^{4}$

Аналогичная группа $\mathbb {C} ^{3}$ или [1 1 1] ^(p) определяется 3 унитарными отражениями периода 2 {R ₁ , R ₂ , R ₃ }: R ₁² = R ₁² = R ₃² = (R ₁ R ₂ ) ³ = (R ₂ R ₃ ) ³ = (R ₃ R ₁ ) ³ = (R ₁ R ₂ R ₃ R ₂ ) ^p = 1.

См. Также [ править ]

Группа Коксетера
Треугольник Шварца
Тетраэдр Гурса
Диаграмма Дынкина
Равномерный многогранник
- Символ Wythoff
- Равномерный многогранник
- Список равномерных многогранников
- Список однородных плоских мозаик
- Равномерный 4-многогранник
- Выпуклые однородные соты
- Выпуклые однородные соты в гиперболическом пространстве
Построение визоффа и символ Wythoff

Ссылки [ править ]

^ Холл, Брайан К. (2003), Группы Ли, алгебры Ли и представления: элементарное введение , Springer, ISBN 978-0-387-40122-5
↑ Coxeter, Regular Polytopes , (3-е издание, 1973), Dover edition, ISBN 0-486-61480-8 , раздел 7.7. стр. 133, Критерий Шлефли
^ Ланнер Ф., О комплексах с транзитивными группами автоморфизмов , Medd. Lunds Univ. Мат. Сем. [Комм. Сем. Математика. Univ. Лунд], 11 (1950), 1–71.
^ Оллкок, Daniel (11 июля 2006). «Бесконечно много гиперболических групп Кокстера через размерность 19». Геометрия и топология . 10 (2): 737–758. arXiv : 0903.0138 . DOI : 10,2140 / gt.2006.10.737 .
^ Геометрия и топология групп Кокстера , Майкл В. Дэвис, 2008 стр. 105 Таблица 6.2. Гиперболические диаграммы
^ Takeuchi, Kisao (январь 1977). «ТАКЕУЧИ: Арифметические группы треугольников» . Журнал математического общества Японии . Projecteuclid.org. 29 (1): 91–106. DOI : 10.2969 / jmsj / 02910091 . Проверено 5 июля 2013 .
^ Фольке Ланнер, О комплексах с транзитивными группами автоморфизмов, Comm. Sém., Math. Univ. Лунд [Medd. Lunds Univ. Мат. Сем.] 11 (1950) [1]
↑ Обычные соты в гиперболическом пространстве , Кокстер, 1954 г.
^ a b Норман Джонсон, Геометрии и преобразования (2018), Глава 13: Гиперболические группы Кокстера, 13.6 Лоренцевы решетки
^ JL Koszul, Лекции по гиперболическим группам Кокстера , Университет Нотр-Дам (1967)
^ M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d'ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), вып. Сер. Р-3, 3–16 (французский). [2]
^ Подалгебры гиперболических алгебр Кея-Муди , рис. 5.1, стр.13
^ Джонсон, NW; Kellerhals, R .; Рэтклифф, Дж. Г.; Чанц, СТ (2002). «Классы соизмеримости гиперболических групп Кокстера» . Линейная алгебра и ее приложения . 345 (1–3): 119–147. DOI : 10.1016 / S0024-3795 (01) 00477-3 .
^ F. Esselmann, Классификация компактных гиперболических d-многогранников Кокстера с d + 2 фасет. Комментарий. Математика. Helvetici 71 (1996), 229–242. [3]
^ И. М. Каплинская, Дискретные группы, порожденные отражениями в гранях симплициальных призм в пространствах Лобачевского. Математика. Примечания, 15 (1974), 88–91. [4]
^ П. Тумаркин, Гиперболические n-многогранники Кокстера с n + 2 гранями (2003)
^ Норман В. Джонсон и Азия Ивич Вайс, Квадратичные целые числа и группы Кокстера , Can. J. Math. Vol. 51 (6), 1999, стр. 1307–1336 [5]
^ [6] Классификация некомпактных многогранников Кокстера с n + 3 гранями и одной непростой вершиной
^ П. Тумаркин, Компактный гиперболический Кокстер (2004)
^ В. О. Бугаенко, Группы автоморфизмов унимодулярных гиперболических квадратичных форм над кольцом Zh√5 + 12 i. Московский унив. Математика. Бык. 39 (1984), 6-14.
^ Анна Феликсон, Павел Тумаркин, О компактных гиперболических d-многогранниках Кокстера с d + 4 гранями , 2005 [7]
↑ Случайные группы, бриллианты и стекло , Дэнни Калегари из Чикагского университета, 25 июня 2014 г., на конференции по наследию Билла Терстона.
^ Кокстеровские группы и случайные группы , Дэнни Калегари, последняя редакция 4 Апрель 2015
^ Максвелл, Джордж (1982). «Сферические упаковки и гиперболические группы отражений» . Журнал алгебры . 79 : 78–97. DOI : 10.1016 / 0021-8693 (82) 90318-0 .
^ Хао Чен, Жан-Филипп Лаббе, группы Лоренциана Кокстера и шариковые упаковки Бойда-Максвелла , https://arxiv.org/abs/1310.8608
^ Алгебры Каца-Муди в M-теории
^ Картана-Gram детерминанты для простых групп Ли , Ву, Альфред С. Т, Американский институт физики, ноябрь 1982
^ Джон Crisp , « карты Инъективные между группами Артиновых », в Даун под теории групп, Труды специального года по геометрической теории групп (Австралийский национальный университет, Канберра, Австралия, 1996), Postscript архивации 2005-10-16 в Вайбак Машина , стр. 13-14, и googlebook, Геометрическая теория групп внизу, стр. 131
^ Зубер, Жан-Бернар (1998). «Обобщенные диаграммы Дынкина и корневые системы и их складки». Топологическая теория поля : 28–30. arXiv : hep-th / 9707046 . Bibcode : 1998tftp.conf..453Z . CiteSeerX 10.1.1.54.3122 .
^ Dechant, Пьер-Филипп; Бем, Селин; Тварок, Рейдун (2013). «Аффинные расширения некристаллографических групп Кокстера, индуцированные проекцией». Журнал математической физики . 54 (9): 093508. arXiv : 1110.5228 . Bibcode : 2013JMP .... 54i3508D . DOI : 10.1063 / 1.4820441 .
^ Е8 Геометрия из Clifford перспективы достижения в области прикладной алгебры Клиффорда , март 2017, том 27, выпуск 1, стр 397-421 Pierre-Philippe Dechant
^ Кокстер, Комплексные регулярные многогранники , второе издание, (1991)
^ Кокстер, Комплексные регулярные многогранники, стр. 177, таблица III
^ Унитарные группы отражений , стр.87

Дальнейшее чтение [ править ]

Джеймс Э. Хамфрис, Группы отражения и группы Кокстера , Кембриджские исследования по высшей математике, 29 (1990)
Калейдоскопы: Избранные сочинения HSM Coxeter , отредактированные Ф. Артуром Шерком, Питером Макмалленом, Энтони С. Томпсоном, Азией Ивичем Вайс, публикацией Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [8] , Googlebooks [ 9]
- (Paper 17) Coxeter , The Evolution of Coxeter-Dynkin diagrams , [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 978-0-486-40919-1 (Глава 3: Построение Витхоффом однородных многогранников)
Коксетер , Правильные многогранники (1963), компания Macmillan
- Регулярные многогранники , третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (Глава 5: Калейдоскоп и Раздел 11.3, Представление графами)
HSM Coxeter и WOJ Moser. Генераторы и соотношения для дискретных групп 4-е изд., Springer-Verlag. Нью-Йорк. 1980 г.
Норман Джонсон , Геометрии и преобразования , главы 11,12,13, препринт 2011 г.
Н. В. Джонсон , Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера , Группы преобразований, 1999, том 4, выпуск 4, стр. 329–353 [10] [11]
Норман У. Джонсон и Асия Ивич Вейсс Квадратичные целые числа и группы Кокстера PDF Can. J. Math. Vol. 51 (6), 1999, с. 1307–1336

Внешние ссылки [ править ]

Викискладе есть медиафайлы, связанные с диаграммами Кокстера-Дынкина .

Вайсштейн, Эрик В. "Диаграмма Кокстера-Дынкина" . MathWorld .
Октябрь 1978 г. дискуссия Кокстера и Дынкина по истории диаграмм Кокстера в Торонто , Канада ; Юджин Дынкин Сборник математических интервью, Библиотека Корнельского университета .

[1] Холл, Брайан К. (2003), Группы Ли, алгебры Ли и представления: элементарное введение , Springer, ISBN 978-0-387-40122-5

[2] Coxeter, Regular Polytopes , (3-е издание, 1973), Dover edition, ISBN 0-486-61480-8 , раздел 7.7. стр. 133, Критерий Шлефли

[3] Ланнер Ф., О комплексах с транзитивными группами автоморфизмов , Medd. Lunds Univ. Мат. Сем. [Комм. Сем. Математика. Univ. Лунд], 11 (1950), 1–71.

[4] Оллкок, Daniel (11 июля 2006). «Бесконечно много гиперболических групп Кокстера через размерность 19». Геометрия и топология . 10 (2): 737–758. arXiv : 0903.0138 . DOI : 10,2140 / gt.2006.10.737 .

[5] Геометрия и топология групп Кокстера , Майкл В. Дэвис, 2008 стр. 105 Таблица 6.2. Гиперболические диаграммы

[6] Takeuchi, Kisao (январь 1977). «ТАКЕУЧИ: Арифметические группы треугольников» . Журнал математического общества Японии . Projecteuclid.org. 29 (1): 91–106. DOI : 10.2969 / jmsj / 02910091 . Проверено 5 июля 2013 .

[7] Фольке Ланнер, О комплексах с транзитивными группами автоморфизмов, Comm. Sém., Math. Univ. Лунд [Medd. Lunds Univ. Мат. Сем.] 11 (1950) [1]

[8] Обычные соты в гиперболическом пространстве , Кокстер, 1954 г.

[johnson2018-9] Норман Джонсон, Геометрии и преобразования (2018), Глава 13: Гиперболические группы Кокстера, 13.6 Лоренцевы решетки

[10] JL Koszul, Лекции по гиперболическим группам Кокстера , Университет Нотр-Дам (1967)

[11] M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d'ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), вып. Сер. Р-3, 3–16 (французский). [2]

[12] Подалгебры гиперболических алгебр Кея-Муди , рис. 5.1, стр.13

[13] Джонсон, NW; Kellerhals, R .; Рэтклифф, Дж. Г.; Чанц, СТ (2002). «Классы соизмеримости гиперболических групп Кокстера» . Линейная алгебра и ее приложения . 345 (1–3): 119–147. DOI : 10.1016 / S0024-3795 (01) 00477-3 .

[14] F. Esselmann, Классификация компактных гиперболических d-многогранников Кокстера с d + 2 фасет. Комментарий. Математика. Helvetici 71 (1996), 229–242. [3]

[15] И. М. Каплинская, Дискретные группы, порожденные отражениями в гранях симплициальных призм в пространствах Лобачевского. Математика. Примечания, 15 (1974), 88–91. [4]

[16] П. Тумаркин, Гиперболические n-многогранники Кокстера с n + 2 гранями (2003)

[17] Норман В. Джонсон и Азия Ивич Вайс, Квадратичные целые числа и группы Кокстера , Can. J. Math. Vol. 51 (6), 1999, стр. 1307–1336 [5]

[18] [6] Классификация некомпактных многогранников Кокстера с n + 3 гранями и одной непростой вершиной

[19] П. Тумаркин, Компактный гиперболический Кокстер (2004)

[20] В. О. Бугаенко, Группы автоморфизмов унимодулярных гиперболических квадратичных форм над кольцом Zh√5 + 12 i. Московский унив. Математика. Бык. 39 (1984), 6-14.

[21] Анна Феликсон, Павел Тумаркин, О компактных гиперболических d-многогранниках Кокстера с d + 4 гранями , 2005 [7]

[22] Случайные группы, бриллианты и стекло , Дэнни Калегари из Чикагского университета, 25 июня 2014 г., на конференции по наследию Билла Терстона.

[23] Кокстеровские группы и случайные группы , Дэнни Калегари, последняя редакция 4 Апрель 2015

[24] Максвелл, Джордж (1982). «Сферические упаковки и гиперболические группы отражений» . Журнал алгебры . 79 : 78–97. DOI : 10.1016 / 0021-8693 (82) 90318-0 .

[25] Хао Чен, Жан-Филипп Лаббе, группы Лоренциана Кокстера и шариковые упаковки Бойда-Максвелла , https://arxiv.org/abs/1310.8608

[26] Алгебры Каца-Муди в M-теории

[27] Картана-Gram детерминанты для простых групп Ли , Ву, Альфред С. Т, Американский институт физики, ноябрь 1982

[28] Джон Crisp , « карты Инъективные между группами Артиновых », в Даун под теории групп, Труды специального года по геометрической теории групп (Австралийский национальный университет, Канберра, Австралия, 1996), Postscript архивации 2005-10-16 в Вайбак Машина , стр. 13-14, и googlebook, Геометрическая теория групп внизу, стр. 131

[29] Зубер, Жан-Бернар (1998). «Обобщенные диаграммы Дынкина и корневые системы и их складки». Топологическая теория поля : 28–30. arXiv : hep-th / 9707046 . Bibcode : 1998tftp.conf..453Z . CiteSeerX 10.1.1.54.3122 .

[30] Dechant, Пьер-Филипп; Бем, Селин; Тварок, Рейдун (2013). «Аффинные расширения некристаллографических групп Кокстера, индуцированные проекцией». Журнал математической физики . 54 (9): 093508. arXiv : 1110.5228 . Bibcode : 2013JMP .... 54i3508D . DOI : 10.1063 / 1.4820441 .

[31] Е8 Геометрия из Clifford перспективы достижения в области прикладной алгебры Клиффорда , март 2017, том 27, выпуск 1, стр 397-421 Pierre-Philippe Dechant

[32] Кокстер, Комплексные регулярные многогранники , второе издание, (1991)

[33] Кокстер, Комплексные регулярные многогранники, стр. 177, таблица III

[34] Унитарные группы отражений , стр.87

[1]