Кристаллографическая теорема ограничения

В этой статье отсутствует информация о сжатой формулировке теоремы . Разверните статью, чтобы включить эту информацию. Более подробная информация может быть на странице обсуждения . ( Декабрь 2018 г. )

Теорема кристаллографического ограничения в своей основной форме была основана на наблюдении , что вращательные симметрии из в кристалле , как правило , ограничены в 2 раз, 3 раза, в 4 раза, а в 6 раз. Однако квазикристаллы могут иметь другую симметрию дифракционной картины, например, 5-кратную; они не были обнаружены до 1982 года Дэном Шехтманом . ^[1]

Кристаллы моделируются как дискретные решетки , порожденные списком независимых конечных перемещений ( Coxeter 1989 ). Поскольку дискретность требует, чтобы расстояния между точками решетки имели нижнюю границу, группа вращательных симметрий решетки в любой точке должна быть конечной группой (альтернативно, точка - единственная система, допускающая бесконечную вращательную симметрию). Сила теоремы в том, что не все конечные группы совместимы с дискретной решеткой; в любом измерении у нас будет только конечное число совместимых групп.

Размеры 2 и 3 [ править ]

Особые случаи 2D ( группы обоев ) и 3D ( пространственные группы ) наиболее широко используются в приложениях, и их можно рассматривать вместе.

Доказательство решетки [ править ]

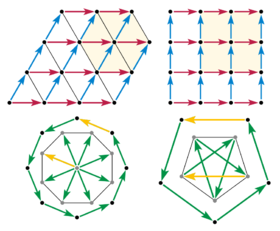
Симметрия вращения в размерности 2 или 3 должна перемещать точку решетки к последовательности других точек решетки в той же плоскости, создавая правильный многоугольник из точек компланарной решетки. Теперь мы ограничиваем наше внимание плоскостью, в которой действует симметрия ( Scherrer 1946 ), проиллюстрированной векторами решетки на рисунке.

Решетки ограничивают многоугольники
 Совместимость : 6-кратная (3-кратная), 4-кратная (2-кратная)
 Несовместимая : 8-кратная, 5-кратная

Теперь рассмотрим 8-кратный поворот и векторы смещения между соседними точками многоугольника. Если между любыми двумя точками решетки существует смещение, то такое же смещение повторяется везде в решетке. Итак, соберите все смещения краев, чтобы начать с одной точки решетки. Эти краевые векторы стали радиальными векторами, и их 8-кратная симметрия предполагает правильный восьмиугольник целых точек вокруг точки сбора. Но это невозможно , потому что новый восьмиугольник примерно на 80% больше оригинала. Значение сжатия в том, что оно безгранично. Эту же конструкцию можно повторять с новым восьмиугольником, и снова и снова, пока расстояние между точками решетки не станет настолько маленьким, насколько нам нравится; таким образом, нет дискретныхрешетка может иметь 8-кратную симметрию. Тот же аргумент применим к любому k -кратному повороту для k больше 6.

Аргумент сокращения также устраняет 5-кратную симметрию. Рассмотрим правильный пятиугольник из точек решетки. Если он существует, то мы можем взять любое другое смещение края и (голова к хвосту) собрать пятиконечную звезду, причем последнее ребро вернется в исходную точку. Вершины такой звезды снова являются вершинами правильного пятиугольника с 5-кратной симметрией, но примерно на 60% меньше исходного.

Таким образом, теорема доказана.

Существование квазикристаллов и мозаик Пенроуза показывает, что предположение о линейном переносе необходимо. Тайлинги Пенроуза могут иметь 5-кратную вращательную симметриюи дискретная решетка, и любая локальная окрестность мозаики повторяется бесконечно много раз, но нет линейного переноса для мозаики в целом. А без предположения о дискретной решетке вышеупомянутая конструкция не только не приводит к противоречию, но и дает (недискретный) контрпример. Таким образом, 5-кратная вращательная симметрия не может быть устранена аргументом, в котором отсутствует одно из этих предположений. Замощение Пенроуза всей (бесконечной) плоскости может иметь точную 5-кратную вращательную симметрию (всего разбиения) относительно одной точки, в то время как 4-кратная и 6-кратная решетки имеют бесконечно много центров вращательной симметрии.

Доказательство тригонометрии [ править ]

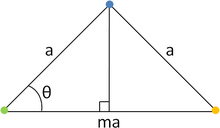
Рассмотрим две точки решетки A и B, разделенные вектором трансляции r . Рассмотрим угол α такой, что поворот на угол α относительно любой точки решетки является симметрией решетки. Вращение вокруг точки B на α отображает точку A в новую точку A '. Аналогично, поворот вокруг точки A на α отображает B в точку B '. Поскольку оба упомянутых поворота являются операциями симметрии, A 'и B' должны быть точками решетки. Из-за периодичности кристалла новый вектор r ', который их соединяет, должен быть равен целому числу, кратному r :

${\displaystyle \mathbf {r} '=m\mathbf {r} }$

с целым числом. Четыре вектора трансляции, три длины и один, соединяющий A 'и B' длины , образуют трапецию. Следовательно, длина r ' также определяется выражением:${\displaystyle m}$${\displaystyle r=|\mathbf {r} |}$${\displaystyle r'=|\mathbf {r} '|}$

${\displaystyle r'=2r\cos \alpha -r.}$

Объединение двух уравнений дает:

${\displaystyle \cos \alpha ={\frac {m+1}{2}}={\frac {M}{2}}}$

где также целое число. Имея в виду, что мы разрешили целые числа . Поиск возможных значений показывает, что единственными значениями в диапазоне от 0 ° до 180 ° являются 0 °, 60 °, 90 °, 120 ° и 180 °. В радианах единственные разрешенные повороты, согласующиеся с периодичностью решетки, задаются соотношением 2π / n , где n = 1, 2, 3, 4, 6. Это соответствует 1-, 2-, 3-, 4- и 6-кратному симметрии, соответственно, и, следовательно, исключает возможность 5-кратной или более чем 6-кратной симметрии.${\displaystyle M=m+1}$${\displaystyle |\cos \alpha |\leq 1}$${\displaystyle M\in \{-2,-1,0,1,2\}}$${\displaystyle \alpha }$

Краткое тригонометрическое доказательство [ править ]

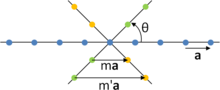
Рассмотрим линию атомов AOB , разделенных расстоянием a . Поверните всю строку на θ = + 2π / n и θ = −2π / n , сохраняя точку O фиксированной. После поворота на + 2π / п , А перемещается в решетке точки С и после поворота на -2π / п , В перемещается к точке решетки D . Из-за предполагаемой периодичности решетки две точки решетки C и D также будут на одной линии непосредственно под начальной строкой; кроме того, C и D будут разделены r = ma , причемm целое число. Но по геометрии расстояние между этими точками составляет:

${\displaystyle 2a\cos {\theta }=2a\cos {\frac {2\pi }{n}}}$.

Приравнивание этих двух отношений дает:

${\displaystyle 2\cos {\frac {2\pi }{n}}=m}$

Этому удовлетворяют только n = 1, 2, 3, 4, 6.

Матричное доказательство [ править ]

В качестве альтернативного доказательства рассмотрим свойства матрицы . Сумма диагональных элементов матрицы называется следом матрицы. В 2D и 3D каждое вращение является плоскостным вращением, и след является функцией только угла. Для двухмерного вращения след равен 2 cos θ; для трехмерного вращения 1 + 2 cos θ.

Примеры

• Рассмотрим матрицу поворота на 60 ° (6-кратного) относительно ортонормированного базиса в 2D.

${\displaystyle {\begin{bmatrix}{1/2}&-{{\sqrt {3}}/2}\\{{\sqrt {3}}/2}&{1/2}\end{bmatrix}}}$

След ровно 1, целое число .

• Рассмотрим матрицу поворота на 45 ° (8-кратную).

${\displaystyle {\begin{bmatrix}{1/{\sqrt {2}}}&-{1/{\sqrt {2}}}\\{1/{\sqrt {2}}}&{1/{\sqrt {2}}}\end{bmatrix}}}$

След составляет 2 / √ 2 , а не целое число.

Выбор базиса, образованного из векторов, охватывающих решетку, не гарантирует ни ортогональности, ни единичной длины, только линейную независимость. Однако след матрицы вращения одинаков для любого базиса. След является инвариантом подобия относительно линейных преобразований. В базисе решетки операция вращения должна отображать каждую точку решетки в целое число векторов решетки, поэтому элементы матрицы вращения в базисе решетки - и, следовательно, след - обязательно являются целыми числами. Как и в других доказательствах, это означает, что единственные разрешенные симметрии вращения соответствуют 1,2,3,4 или 6-кратной инвариантности. Например, обои и кристаллы не могут поворачиваться на 45 ° и оставаться неизменными, возможны только углы: 360 °, 180 °, 120 °, 90 ° или 60 °.

Пример

• Рассмотрим матрицу поворота на 60 ° (360 ° / 6) относительно базиса наклонной решетки для замощения равносторонними треугольниками.

${\displaystyle {\begin{bmatrix}0&-1\\1&1\end{bmatrix}}}$

След по-прежнему равен 1. Определитель (всегда +1 для вращения) также сохраняется.

Общее кристаллографическое ограничение на вращение не гарантирует, что вращение будет совместимо с конкретной решеткой. Например, поворот на 60 ° не подойдет для квадратной решетки; и поворот на 90 ° не будет работать с прямоугольной решеткой.

Высшие измерения [ править ]

Когда размер решетки увеличивается до четырех или более, повороты больше не должны быть плоскими; 2D-доказательство неадекватно. Однако ограничения по-прежнему действуют, хотя допускается большее количество симметрий. Например, гиперкубическая решетка имеет восьмеричную вращательную симметрию, соответствующую восьмикратной вращательной симметрии гиперкуба . Это представляет интерес не только для математики, но и для физики квазикристаллов в рамках теории разреза и проекции . С этой точки зрения трехмерный квазикристалл с 8-кратной симметрией вращения может быть описан как проекция плиты, вырезанной из четырехмерной решетки.

Следующая матрица четырехмерного вращения представляет собой вышеупомянутую восьмикратную симметрию гиперкуба (и кросс-политопа ):

${\displaystyle A={\begin{bmatrix}0&0&0&-1\\1&0&0&0\\0&-1&0&0\\0&0&-1&0\end{bmatrix}}.}$

Преобразование этой матрицы в новые координаты, заданные

${\displaystyle B={\begin{bmatrix}-1/2&0&-1/2&{\sqrt {2}}/2\\1/2&{\sqrt {2}}/2&-1/2&0\\-1/2&0&-1/2&-{\sqrt {2}}/2\\-1/2&{\sqrt {2}}/2&1/2&0\end{bmatrix}}}$ произведет:

${\displaystyle BAB^{-1}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\-{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\0&0&-{\sqrt {2}}/2&{\sqrt {2}}/2\\0&0&-{\sqrt {2}}/2&-{\sqrt {2}}/2\end{bmatrix}}.}$

Эта третья матрица соответствует повороту как на 45 ° (в первых двух измерениях), так и на 135 ° (в последних двух). При проецировании плиты гиперкубов по первым двум измерениям новых координат получается мозаика Амманна – Бенкера (другая такая мозаика создается путем проецирования по последним двум измерениям), которая, следовательно, также имеет в среднем 8-кратную вращательную симметрию.

А4 решетки и F4 решетки имеют порядок 10 и порядка 12 вращательные симметрии, соответственно.

Чтобы установить ограничение для всех измерений, удобно отвлечь внимание от одних только вращений и сконцентрироваться на целочисленных матрицах ( Bamberg, Cairns & Kilminster, 2003 ). Мы говорим, что матрица A имеет порядок k, когда ее k -я степень (но не меньшая), A ^k , равна единице. Таким образом, матрица 6-кратного вращения в базисе равностороннего треугольника является целочисленной матрицей с порядком 6. Пусть Ord _N обозначает набор целых чисел, которые могут быть порядком целочисленной матрицы N × N. Например, Ord ₂ = {1, 2, 3, 4, 6}. Мы хотели бы отметить , явную формулу для Ord _N .

Определите функцию ψ, основанную на функции Эйлера φ; он будет отображать положительные целые числа в неотрицательные целые числа. Для нечетного простого числа , р , и положительного целого числа, к , множество ψ ( р ^к ) равен значению функции totient, φ ( р ^K ), который в данном случае является р ^к - р ^К-1 . Сделайте то же самое для ψ (2 ^k ), когда k > 1. Установите ψ (2) и ψ (1) в 0. Используя основную теорему арифметики , мы можем записать любое другое положительное целое число однозначно как произведение степеней простых чисел, m = ∏ _α p _α^{k _α} ; Положим ψ (m) = ∑_αψ (p_α ^{k _α} ). Это отличается от самого totient, потому что это сумма, а не продукт.

Кристаллографическое ограничение в общем виде гласит , что Ord _Н состоит из тех положительных целых чисел т таким образом, что ψ ( м ) ≤ N .

Наименьший размер для данного заказа OEIS :  A080737

м	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21 год	22	23	24	25	26	27	28	29	30	31 год
ψ ( м )	0	0	2	2	4	2	6	4	6	4	10	4	12	6	6	8	16	6	18	6	8	10	22	6	20	12	18	8	28	6	30

При m > 2 значения ψ ( m ) равны удвоенной алгебраической степени cos (2π / m ); Таким образом, ψ ( м ) строго меньше м и достигает этого максимальное значение , если и только если т является простым .

Эти дополнительные симметрии не позволяют плоскому срезу иметь, скажем, 8-кратную симметрию вращения. В плоскости все еще действуют ограничения 2D. Таким образом, вырезы, используемые для моделирования квазикристаллов, обязательно имеют толщину.

Целочисленные матрицы не ограничиваются поворотами; например, отражение также является симметрией порядка 2. Но, настаивая на определителе +1, мы можем ограничить матрицы правильным вращением .

Формулировка в терминах изометрий [ править ]

Теорема кристаллографического ограничения может быть сформулирована в терминах изометрий в евклидове пространства . Набор изометрий может образовывать группу . Под дискретной группой изометрий мы будем понимать группу изометрий, которая отображает каждую точку в дискретное подмножество R ^N , т. Е. Орбита любой точки является набором изолированных точек . Используя эту терминологию, кристаллографическая теорема ограничения в двух и трех измерениях может быть сформулирована следующим образом.

Для каждой дискретной группы изометрий в двух- и трехмерном пространстве, которая включает трансляции, охватывающие все пространство, все изометрии конечного порядка имеют порядок 1, 2, 3, 4 или 6.

Изометрии порядка n включают n- кратные повороты , но не ограничиваются ими . Теорема также исключает S ₈ , S ₁₂ , D _4d и D _6d (см. Точечные группы в трех измерениях ), хотя они обладают только 4- и 6-кратной вращательной симметрией. Вращательная симметрия любого порядка относительно оси совместима с трансляционной симметрией вдоль этой оси.

Результат в таблице выше означает, что для каждой дискретной группы изометрий в четырех- и пятимерном пространстве, которая включает трансляции, охватывающие все пространство, все изометрии конечного порядка имеют порядок 1, 2, 3, 4, 5, 6, 8. , 10 или 12.

Все изометрии конечного порядка в шестимерном и семимерном пространстве имеют порядок 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 или 30.

См. Также [ править ]

• Кристаллографическая точечная группа
• Кристаллография

Примечания [ править ]

Ссылки [ править ]

• Бамберг, Джон; Кэрнс, Грант; Kilminster, Девин (март 2003 г.), "кристаллографической ограничение, Перестановки и Гольдбаха гипотеза" (PDF) , American Mathematical Monthly , 110 (3): 202-209, CiteSeerX  10.1.1.124.8582 , DOI : 10,2307 / 3647934 , JSTOR  3647934
• Эллиотт, Стивен (1998), Физика и химия твердых тел , Wiley, ISBN 978-0-471-98194-7
• Кокстер, HSM (1989), Введение в геометрию (2-е изд.), Wiley, ISBN 978-0-471-50458-0
• Шеррер В. (1946), "Die Einlagerung eines Regären Vielecks in ein Gitter" , Elemente der Mathematik , 1 (6): 97–98
• Шехтман, Д .; Blech, I .; Gratias, D .; Кан, Дж. У. (1984), «Металлическая фаза с дальним ориентационным порядком и без трансляционной симметрии», Physical Review Letters , 53 (20): 1951–1953, Bibcode : 1984PhRvL..53.1951S , doi : 10.1103 / PhysRevLett.53.1951

Внешние ссылки [ править ]

• Кристаллографическое ограничение