Неравенство средних арифметических и геометрических

Доказательство без слов в неравенство арифметических и средних геометрических :
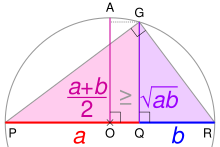
PR - представляет собой диаметр окружности с центром на О; его радиус АО является средним арифметическим из и б . Используя теорему о среднем геометрическом , высота GQ треугольника PGR является средним геометрическим . Для любого коэффициента а : Ь , АО ≥ GQ.

Наглядное доказательство того, что ( x + y ) ² ≥ 4 xy . Извлечение квадратного корня и деление на два дает неравенство AM – GM. ^[1]

В математике , то неравенство арифметических и геометрических средств , или более кратко в неравенстве AM-GM , утверждает , что среднее арифметическое из списка неотрицательных действительных чисел больше или равно среднему геометрическому из того же списка; и далее, что два средних значения равны тогда и только тогда, когда все числа в списке одинаковы.

Простейшим нетривиальным случаем, т. Е. С более чем одной переменной, для двух неотрицательных чисел x и  y является утверждение, что

${\ displaystyle {\ frac {x + y} {2}} \ geq {\ sqrt {xy}}}$

с равенством тогда и только тогда, когда x = y . Этот случай можно увидеть из того факта, что квадрат действительного числа всегда неотрицателен (больше или равен нулю), и из элементарного случая ( a ± b ) ² = a ² ± 2 ab + b ² числа биномиальная формула :

${\ displaystyle {\ begin {align} 0 & \ leq (xy) ^ {2} \\ & = x ^ {2} -2xy + y ^ {2} \\ & = x ^ {2} + 2xy + y ^ {2} -4xy \\ & = (x + y) ^ {2} -4xy. \ End {align}}}$

Следовательно, ( x + y ) ² ≥ 4 xy с равенством в точности тогда, когда ( x - y ) ² = 0 , т.е. x = y . Тогда неравенство AM – GM следует из извлечения положительного квадратного корня из обеих частей и последующего деления обеих частей на 2 .

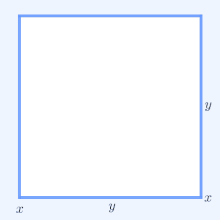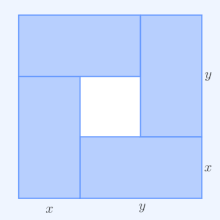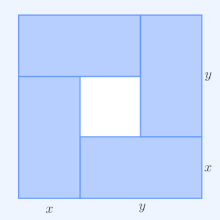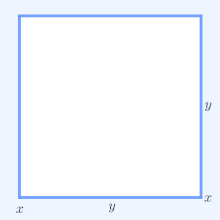
Для геометрической интерпретации рассмотрим прямоугольник со сторонами длиной  x и  y , следовательно, он имеет периметр 2 x + 2 y и площадь  xy . Точно так же квадрат со всеми сторонами длиной √ xy имеет периметр 4 √ xy и такую ​​же площадь, что и прямоугольник. В простейшем нетривиальном случае неравенства AM – GM для периметров следует, что 2 x + 2 y ≥ 4 √ xy и что только квадрат имеет наименьший периметр среди всех прямоугольников одинаковой площади.

Доступны расширения неравенства AM – GM для включения весов или обобщенных средних .

Фон [ править ]

Среднее арифметическое , или менее точно среднем , из списка п чисел х ₁ , х ₂ ,. . . , x _n - сумма чисел, деленная на  n :

${\ displaystyle {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}}.}$

Среднее геометрическое аналогично, за исключением того, что она определена только для списка неотрицательных действительных чисел, и использует умножение и корень вместо сложения и деления:

${\ displaystyle {\ sqrt [{n}] {x_ {1} \ cdot x_ {2} \ cdots x_ {n}}}.}.$

Если x ₁ , x ₂ ,. . . , x _n > 0 , это равно экспоненте среднего арифметического натуральных логарифмов чисел:

${\ displaystyle \ exp \ left ({\ frac {\ ln {x_ {1}} + \ ln {x_ {2}} + \ cdots + \ ln {x_ {n}}} {n}} \ right). }$

Неравенство [ править ]

Повторяя неравенство с использованием математической записи, мы имеем, что для любого списка из n неотрицательных действительных чисел x ₁ , x ₂ ,. . . , x _n ,

${\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}\,,}$

и что равенство выполняется тогда и только тогда, когда x ₁ = x ₂ = · · · = x _n .

Геометрическая интерпретация [ править ]

В двух измерениях 2 x ₁ + 2 x ₂ - это периметр прямоугольника со сторонами длиной  x ₁ и  x ₂ . Аналогичным образом , 4 √ х ₁ х ₂ периметр квадрата с одной и той же области , х ₁ х ₂ , так как этот прямоугольник. Таким образом, для n = 2 неравенство AM – GM утверждает, что прямоугольник заданной площади имеет наименьший периметр, если этот прямоугольник также является квадратом.

Полное неравенство - это расширение этой идеи до n измерений. Каждая вершина n- мерного ящика соединена с n ребрами. Если длины этих ребер равны x ₁ , x ₂ ,. . . , x _n , то x ₁ + x ₂ + · · · + x _n - общая длина ребер, инцидентных вершине. Имеется 2 ⁿ вершин, поэтому мы умножаем это на  2 ⁿ ; однако, поскольку каждое ребро пересекает две вершины, каждое ребро считается дважды. Поэтому делим на  2и заключаем, что имеется 2 ^{n −1} n ребер. Имеется одинаковое количество ребер каждой длины и длины n ; следовательно, имеется 2 ^{n −1} ребра каждой длины, а сумма всех длин ребер равна 2 ^{n −1} ( x ₁ + x ₂ + · · · + x _n ) . С другой стороны,

${\displaystyle 2^{n-1}(x_{1}+\ldots +x_{n})=2^{n-1}n{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$

- общая длина ребер, соединенных с вершиной n- мерного куба равного объема, так как в этом случае x ₁ = ... = x _n . Поскольку неравенство говорит

${\displaystyle {x_{1}+x_{2}+\cdots +x_{n} \over n}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}},}$

его можно пересчитать, умножив на n 2 ^{n –1,} чтобы получить

${\displaystyle 2^{n-1}(x_{1}+x_{2}+\cdots +x_{n})\geq 2^{n-1}n{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$

с равенством тогда и только тогда, когда x ₁ = x ₂ = · · · = x _n .

Таким образом, неравенство AM – GM утверждает, что только n -куб имеет наименьшую сумму длин ребер, соединенных с каждой вершиной, среди всех n -мерных ящиков с одинаковым объемом. ^[2]

Пример приложения [ править ]

Рассмотрим функцию

${\displaystyle f(x,y,z)={\frac {x}{y}}+{\sqrt {\frac {y}{z}}}+{\sqrt[{3}]{\frac {z}{x}}}}$

для всех положительных действительных чисел x , y и  z . Предположим, мы хотим найти минимальное значение этой функции. Сначала немного перепишем:

${\displaystyle {\begin{aligned}f(x,y,z)&=6\cdot {\frac {{\frac {x}{y}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}{6}}\\&=6\cdot {\frac {x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}}{6}}\end{aligned}}}$

с

${\displaystyle x_{1}={\frac {x}{y}},\qquad x_{2}=x_{3}={\frac {1}{2}}{\sqrt {\frac {y}{z}}},\qquad x_{4}=x_{5}=x_{6}={\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}.}$

Применяя неравенство AM – GM для n = 6 , получаем

${\displaystyle {\begin{aligned}f(x,y,z)&\geq 6\cdot {\sqrt[{6}]{{\frac {x}{y}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}}\\&=6\cdot {\sqrt[{6}]{{\frac {1}{2\cdot 2\cdot 3\cdot 3\cdot 3}}{\frac {x}{y}}{\frac {y}{z}}{\frac {z}{x}}}}\\&=2^{2/3}\cdot 3^{1/2}.\end{aligned}}}$

Кроме того, мы знаем, что две стороны равны именно тогда, когда все члены среднего равны:

${\displaystyle f(x,y,z)=2^{2/3}\cdot 3^{1/2}\quad {\mbox{when}}\quad {\frac {x}{y}}={\frac {1}{2}}{\sqrt {\frac {y}{z}}}={\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}.}$

Все точки ( x , y , z ), удовлетворяющие этим условиям, лежат на полупрямой, начинающейся в начале координат, и имеют вид

${\displaystyle (x,y,z)={\biggr (}t,{\sqrt[{3}]{2}}{\sqrt {3}}\,t,{\frac {3{\sqrt {3}}}{2}}\,t{\biggr )}\quad {\mbox{with}}\quad t>0.}$

Практическое применение [ править ]

Важным практическим приложением в финансовой математике является вычисление нормы прибыли : годовая доходность , рассчитанная через среднее геометрическое, меньше, чем средняя годовая доходность, вычисленная по среднему арифметическому (или равная, если все доходности равны). Это важно при анализе инвестиций, так как средний доход превышает совокупный эффект.

Доказательства неравенства AM – GM [ править ]

Доказательство с использованием неравенства Дженсена [ править ]

Неравенство Дженсена гласит, что значение вогнутой функции среднего арифметического больше или равно среднему арифметическому значений функции. Поскольку функция логарифма вогнутая, мы имеем

${\displaystyle \log \left({\frac {\sum _{i}x_{i}}{n}}\right)\geq \sum {\frac {1}{n}}\log x_{i}=\sum \left(\log x_{i}^{1/n}\right)=\log \left(\prod x_{i}^{1/n}\right).}$

Взяв антиблоки крайней левой и крайней правой части, мы имеем неравенство AM – GM.

Доказательства по индукции [ править ]

Мы должны показать, что

${\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$

с равенством только тогда, когда все числа равны. Если x _i ≠ x _j , то замена как x _{i, так} и x _j на ( x _i + x _j ) / 2 оставит среднее арифметическое в левой части без изменений, но увеличит среднее геометрическое в правой части. потому что

${\displaystyle {\Bigl (}{\frac {x_{i}+x_{j}}{2}}{\Bigr )}^{2}-x_{i}x_{j}={\Bigl (}{\frac {x_{i}-x_{j}}{2}}{\Bigr )}^{2}>0.}$

Таким образом, правая часть будет наибольшей, когда все x _i s равны среднему арифметическому

${\displaystyle \alpha ={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}},}$

таким образом, поскольку это наибольшее значение правой части выражения, мы имеем

${\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}=\alpha ={\sqrt[{n}]{\alpha \alpha \cdots \alpha }}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}.}$

Это действительное доказательство для случая n = 2 , но процедура итеративного попарного усреднения может не дать n равных чисел в случае n ≥ 3 . Примером этого случая является x ₁ = x ₂ ≠ x ₃ : усреднение двух разных чисел дает два одинаковых числа, но третье по-прежнему отличается. Следовательно, на самом деле мы никогда не получим неравенство, включающее среднее геометрическое трех равных чисел.

Следовательно, необходим дополнительный трюк или модифицированный аргумент, чтобы превратить вышеприведенную идею в действительное доказательство для случая n ≥ 3 .

Доказательство по индукции №1 [ править ]

Из неотрицательных действительных чисел x ₁ ,. . . , x _n , утверждение AM – GM эквивалентно

${\displaystyle \alpha ^{n}\geq x_{1}x_{2}\cdots x_{n}}$

с равенством тогда и только тогда, когда α = x _i для всех i ∈ {1,. . . , n } .

Для следующего доказательства мы применяем математическую индукцию и только хорошо известные правила арифметики.

Базис индукции: для n = 1 утверждение верно с равенством.

Гипотеза индукции: предположим, что утверждение AM – GM выполняется для любого выбора n неотрицательных действительных чисел.

Шаг индукции: Рассмотрим n + 1 неотрицательных действительных чисел x ₁ ,. . . , Х _{п +1} ,. Их среднее арифметическое α удовлетворяет

${\displaystyle (n+1)\alpha =\ x_{1}+\cdots +x_{n}+x_{n+1}.}$

Если все x _i равны α , тогда мы имеем равенство в утверждении AM – GM, и все готово. В случае, когда некоторые из них не равны α , должно существовать одно число, которое больше среднего арифметического α , и другое число меньше α . Без потери общности, мы можем переупорядочить наш x _i , чтобы разместить эти два конкретных элемента в конце: x _n > α и x _{n +1} < α . потом

${\displaystyle x_{n}-\alpha >0\qquad \alpha -x_{n+1}>0}$

${\displaystyle \implies (x_{n}-\alpha )(\alpha -x_{n+1})>0\,.\qquad (*)}$

Теперь определим y с помощью

${\displaystyle y:=x_{n}+x_{n+1}-\alpha \geq x_{n}-\alpha >0\,,}$

и рассмотрим n чисел x ₁ ,. . . , x _{n –1} , y, которые все неотрицательны. С

${\displaystyle (n+1)\alpha =x_{1}+\cdots +x_{n-1}+x_{n}+x_{n+1}}$

${\displaystyle n\alpha =x_{1}+\cdots +x_{n-1}+\underbrace {x_{n}+x_{n+1}-\alpha } _{=\,y},}$

Таким образом, α также является средним арифметическим n чисел x ₁ ,. . . , x _{n –1} , y и предположение индукции влечет

${\displaystyle \alpha ^{n+1}=\alpha ^{n}\cdot \alpha \geq x_{1}x_{2}\cdots x_{n-1}y\cdot \alpha .\qquad (**)}$

Благодаря (*) мы знаем, что

${\displaystyle (\underbrace {x_{n}+x_{n+1}-\alpha } _{=\,y})\alpha -x_{n}x_{n+1}=(x_{n}-\alpha )(\alpha -x_{n+1})>0,}$

следовательно

${\displaystyle y\alpha >x_{n}x_{n+1}\,,\qquad ({*}{*}{*})}$

в частности, α > 0 . Следовательно, если хотя бы одно из чисел x ₁ ,. . . , x _{n –1} равно нулю, то строгое неравенство в (**) уже выполняется. В противном случае правая часть (**) положительна, и строгое неравенство получается путем использования оценки (***) для получения нижней оценки правой части (**). Таким образом, в обоих случаях мы можем заменить (***) на (**), чтобы получить

${\displaystyle \alpha ^{n+1}>x_{1}x_{2}\cdots x_{n-1}x_{n}x_{n+1}\,,}$

что завершает доказательство.

Доказательство по индукции №2 [ править ]

Прежде всего докажем, что для действительных чисел x ₁ <1 и x ₂ > 1 следует

${\displaystyle x_{1}+x_{2}>x_{1}x_{2}+1.}$

Действительно, умножение обеих частей неравенства x ₂ > 1 на 1 - x ₁ дает

${\displaystyle x_{2}-x_{1}x_{2}>1-x_{1},}$

откуда сразу получается требуемое неравенство.

Теперь мы собираемся доказать, что для положительных действительных чисел x ₁ ,. . . , x _n, удовлетворяющее x ₁ . . . x _n = 1 , выполняется

${\displaystyle x_{1}+\cdots +x_{n}\geq n.}$

Равенство выполняется, только если x ₁ = ... = x _n = 1 .

Базис индукции: для n = 2 утверждение верно из-за указанного выше свойства.

Гипотеза индукции: предположим, что утверждение верно для всех натуральных чисел до n - 1 .

Шаг индукции: Рассмотрим натуральное число n , т.е. для положительных действительных чисел x ₁ ,. . . , x _n , выполняется x ₁ . . . х _п = 1 . Существует хотя бы один x _k <1 , поэтому должен быть хотя бы один x _j > 1 . Без ограничения общности положим k = n - 1 и j = n .

Далее, равенство x ₁ . . . x _n = 1 запишем в виде ( x ₁ ... x _{n –2} ) ( x _{n –1} x _n ) = 1 . Тогда из предположения индукции следует

${\displaystyle (x_{1}+\cdots +x_{n-2})+(x_{n-1}x_{n})>n-1.}$

Однако с учетом базиса индукции имеем

${\displaystyle {\begin{aligned}x_{1}+\cdots +x_{n-2}+x_{n-1}+x_{n}&=(x_{1}+\cdots +x_{n-2})+(x_{n-1}+x_{n})\\&>(x_{1}+\cdots +x_{n-2})+x_{n-1}x_{n}+1\\&>n,\end{aligned}}}$

что завершает доказательство.

Для положительных действительных чисел a ₁ ,. . . , a _n , обозначим

${\displaystyle x_{1}={\frac {a_{1}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}},...,x_{n}={\frac {a_{n}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}}.}$

Числа x ₁ ,. . . , x _n удовлетворяют условию x ₁ . . . х _п = 1 . Итак, у нас есть

${\displaystyle {\frac {a_{1}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}}+\cdots +{\frac {a_{n}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}}\geq n,}$

откуда получаем

${\displaystyle {\frac {a_{1}+\cdots +a_{n}}{n}}\geq {\sqrt[{n}]{a_{1}\cdots a_{n}}},}$

причем равенство выполняется только для a ₁ = ... = a _n .

Доказательство Коши с использованием прямой-обратной индукции [ править ]

Следующее ниже доказательство по случаям напрямую опирается на хорошо известные правила арифметики, но использует редко используемую технику прямой-обратной индукции. По сути, это произведение Огюстена Луи Коши, которое можно найти в его Cours d'analyse . ^[3]

Случай, когда все термины равны [ править ]

Если все условия равны:

${\displaystyle x_{1}=x_{2}=\cdots =x_{n},}$

тогда их сумма равна nx ₁ , поэтому их среднее арифметическое равно  x ₁ ; и их произведение равно x ₁ ⁿ , поэтому их среднее геометрическое равно  x ₁ ; следовательно, среднее арифметическое и среднее геометрическое равны, как требуется.

Случай, когда не все термины равны [ править ]

Осталось показать, что если не все члены равны, то среднее арифметическое больше среднего геометрического. Ясно, что это возможно только при n > 1 .

Этот случай значительно сложнее, и мы разбиваем его на подслучаи.

Подслучай, где n = 2 [ править ]

Если n = 2 , то у нас есть два члена, x ₁ и x ₂ , и поскольку (по нашему предположению) не все члены равны, мы имеем:

${\displaystyle {\begin{aligned}{\Bigl (}{\frac {x_{1}+x_{2}}{2}}{\Bigr )}^{2}-x_{1}x_{2}&={\frac {1}{4}}(x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2})-x_{1}x_{2}\\&={\frac {1}{4}}(x_{1}^{2}-2x_{1}x_{2}+x_{2}^{2})\\&={\Bigl (}{\frac {x_{1}-x_{2}}{2}}{\Bigr )}^{2}>0,\end{aligned}}}$

следовательно

${\displaystyle {\frac {x_{1}+x_{2}}{2}}>{\sqrt {x_{1}x_{2}}}}$

по желанию.

Подслучай, где n = 2 ^k [ править ]

Рассмотрим случай, когда n = 2 ^k , где k - натуральное число. Действуем по математической индукции.

В базовом случае k = 1 , поэтому n = 2 . Мы уже показали, что неравенство выполняется при n = 2 , поэтому мы закончили.

Теперь предположим, что для данного k > 1 мы уже показали, что неравенство выполняется для n = 2 ^{k −1} , и мы хотим показать, что оно выполняется для n = 2 ^k . Для этого применим неравенство дважды для 2 ^{k -1} чисел и один раз для 2 чисел, чтобы получить:

${\displaystyle {\begin{aligned}{\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}&{}={\frac {{\frac {x_{1}+x_{2}+\cdots +x_{2^{k-1}}}{2^{k-1}}}+{\frac {x_{2^{k-1}+1}+x_{2^{k-1}+2}+\cdots +x_{2^{k}}}{2^{k-1}}}}{2}}\\[7pt]&\geq {\frac {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}+{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}{2}}\\[7pt]&\geq {\sqrt {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}}\\[7pt]&={\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}\end{aligned}}}$

где в первом неравенстве две стороны равны, только если

${\displaystyle x_{1}=x_{2}=\cdots =x_{2^{k-1}}}$

и

${\displaystyle x_{2^{k-1}+1}=x_{2^{k-1}+2}=\cdots =x_{2^{k}}}$

(в этом случае первое среднее арифметическое и первое среднее геометрическое равны  x ₁ и аналогично со вторым средним арифметическим и вторым средним геометрическим); а во втором неравенстве две стороны равны, только если два средних геометрических равны. Поскольку не все 2 ^k числа равны, невозможно, чтобы оба неравенства были равенствами, поэтому мы знаем, что:

${\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}>{\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}}$

по желанию.

Подслучай, где n <2 ^k [ править ]

Если n не является естественной степенью  двойки , то она определенно меньше некоторой естественной степени двойки, поскольку последовательность 2, 4, 8,. . . , 2 ^к ,. . . неограничен сверху. Поэтому, без ограничения общности, пусть m будет некоторой естественной степенью двойки , большей  n .

Итак, если у нас есть n терминов, то давайте обозначим их среднее арифметическое через  α и расширим наш список терминов следующим образом:

${\displaystyle x_{n+1}=x_{n+2}=\cdots =x_{m}=\alpha .}$

Тогда у нас есть:

${\displaystyle {\begin{aligned}\alpha &={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\\[6pt]&={\frac {{\frac {m}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+{\frac {(m-n)}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+\left(m-n\right)\alpha }{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}+\cdots +x_{m}}{m}}\\[6pt]&>{\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}x_{n+1}\cdots x_{m}}}\\[6pt]&={\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}}}\,,\end{aligned}}}$

так

${\displaystyle \alpha ^{m}>x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}}$

и

${\displaystyle \alpha >{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}$

по желанию.

Доказательство по индукции с использованием основного исчисления [ править ]

Следующее доказательство использует математическую индукцию и некоторые основные дифференциальные исчисления .

Базис индукции : для n = 1 утверждение верно с равенством.

Гипотеза индукции : предположим, что утверждение AM – GM выполняется для любого выбора n неотрицательных действительных чисел.

Шаг индукции : чтобы доказать утверждение для n + 1 неотрицательных действительных чисел x ₁ ,. . . , x _n , x _{n +1} , нам нужно доказать, что

${\displaystyle {\frac {x_{1}+\cdots +x_{n}+x_{n+1}}{n+1}}-({x_{1}\cdots x_{n}x_{n+1}})^{\frac {1}{n+1}}\geq 0}$

с равенством, только если все n + 1 числа равны.

Если все числа равны нулю, неравенство выполняется с равенством. Если некоторые, но не все числа равны нулю, мы имеем строгое неравенство. Поэтому в дальнейшем мы можем считать, что все n + 1 числа положительны.

Рассмотрим последнее число x _{n +1} как переменную и определим функцию

${\displaystyle f(t)={\frac {x_{1}+\cdots +x_{n}+t}{n+1}}-({x_{1}\cdots x_{n}t})^{\frac {1}{n+1}},\qquad t>0.}$

Доказательство шага индукции эквивалентно доказательству того, что f ( t ) ≥ 0 для всех t > 0 , причем f ( t ) = 0, только если x ₁ ,. . . , x _n и  t равны. Это может быть сделано путем анализа критических точек из  F , используя основы исчисления.

Первая производная от f дается формулой

${\displaystyle f'(t)={\frac {1}{n+1}}-{\frac {1}{n+1}}({x_{1}\cdots x_{n}})^{\frac {1}{n+1}}t^{-{\frac {n}{n+1}}},\qquad t>0.}$

Критическая точка t ₀ должна удовлетворять условию f ′ ( t ₀ ) = 0 , что означает

${\displaystyle ({x_{1}\cdots x_{n}})^{\frac {1}{n+1}}t_{0}^{-{\frac {n}{n+1}}}=1.}$

После небольшой переделки получаем

${\displaystyle t_{0}^{\frac {n}{n+1}}=({x_{1}\cdots x_{n}})^{\frac {1}{n+1}},}$

и наконец

${\displaystyle t_{0}=({x_{1}\cdots x_{n}})^{\frac {1}{n}},}$

что является средним геометрическим для x ₁ ,. . . , х _п . Это единственная критическая точка  f . Так как F '' ( т )> 0 для всех т > 0 , то функция  F является строго выпуклой и имеет строгий глобальный минимум при  т ₀ . Затем мы вычисляем значение функции в этом глобальном минимуме:

${\displaystyle {\begin{aligned}f(t_{0})&={\frac {x_{1}+\cdots +x_{n}+({x_{1}\cdots x_{n}})^{1/n}}{n+1}}-({x_{1}\cdots x_{n}})^{\frac {1}{n+1}}({x_{1}\cdots x_{n}})^{\frac {1}{n(n+1)}}\\&={\frac {x_{1}+\cdots +x_{n}}{n+1}}+{\frac {1}{n+1}}({x_{1}\cdots x_{n}})^{\frac {1}{n}}-({x_{1}\cdots x_{n}})^{\frac {1}{n}}\\&={\frac {x_{1}+\cdots +x_{n}}{n+1}}-{\frac {n}{n+1}}({x_{1}\cdots x_{n}})^{\frac {1}{n}}\\&={\frac {n}{n+1}}{\Bigl (}{\frac {x_{1}+\cdots +x_{n}}{n}}-({x_{1}\cdots x_{n}})^{\frac {1}{n}}{\Bigr )}\\&\geq 0,\end{aligned}}}$

где последнее неравенство выполняется в силу предположения индукции. Гипотеза также говорит, что мы можем иметь равенство только тогда, когда x ₁ ,. . . , x _n все равны. В этом случае их среднее геометрическое   t ₀ имеет такое же значение. Следовательно, если x ₁ ,. . . , x _n , x _{n +1} равны, имеем f ( x _{n +1} )> 0 . Это завершает доказательство.

Эту технику можно использовать таким же образом для доказательства обобщенного неравенства AM – GM и неравенства Коши – Шварца в евклидовом пространстве R ⁿ .

Доказательство Полиа с использованием экспоненциальной функции [ править ]

Джордж Полиа представил доказательство, подобное следующему. Пусть f ( x ) = e ^{x –1} - x для всех действительных  x , с первой производной f ′ ( x ) = e ^{x –1} - 1 и второй производной f ′ ′ ( x ) = e ^{x –1} . Заметим, что f (1) = 0 , f ′ (1) = 0 и f ′ ′ ( x )> 0 для всех действительных  x , поэтому f строго выпуклый с абсолютным минимумом вх = 1 . Следовательно, x ≤ e ^{x –1} для всех действительных  x с равенством только для x = 1 .

Рассмотрим список неотрицательных действительных чисел x ₁ , x ₂ ,. . . , х _п . Если все они равны нулю, то неравенство AM – GM выполняется с равенством. Следовательно, в дальнейшем для их среднего арифметического можно считать α > 0 . По п - кратном применении вышеуказанного неравенства, получаем , что

${\displaystyle {\begin{aligned}{{\frac {x_{1}}{\alpha }}{\frac {x_{2}}{\alpha }}\cdots {\frac {x_{n}}{\alpha }}}&\leq {e^{{\frac {x_{1}}{\alpha }}-1}e^{{\frac {x_{2}}{\alpha }}-1}\cdots e^{{\frac {x_{n}}{\alpha }}-1}}\\&=\exp {\Bigl (}{\frac {x_{1}}{\alpha }}-1+{\frac {x_{2}}{\alpha }}-1+\cdots +{\frac {x_{n}}{\alpha }}-1{\Bigr )},\qquad (*)\end{aligned}}}$

с равенством тогда и только тогда, когда x _i = α для любого i ∈ {1,. . . , n } . Аргумент экспоненциальной функции можно упростить:

${\displaystyle {\begin{aligned}{\frac {x_{1}}{\alpha }}-1+{\frac {x_{2}}{\alpha }}-1+\cdots +{\frac {x_{n}}{\alpha }}-1&={\frac {x_{1}+x_{2}+\cdots +x_{n}}{\alpha }}-n\\&={\frac {n\alpha }{\alpha }}-n\\&=0.\end{aligned}}}$

Возвращаясь к (*) ,

${\displaystyle {\frac {x_{1}x_{2}\cdots x_{n}}{\alpha ^{n}}}\leq e^{0}=1,}$

что дает x ₁ x ₂ · · · x _n ≤ α ⁿ , отсюда и результат ^[4]

${\displaystyle {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\leq \alpha .}$

Доказательство с помощью лагранжевых множителей [ править ]

Если таковые имеются , то доказывать нечего. Таким образом, мы можем предположить, что все они строго положительны.${\displaystyle x_{i}}$${\displaystyle 0}$${\displaystyle x_{i}}$

Поскольку средние арифметические и геометрические однородны степени 1, без ограничения общности предположим, что . Установить , и . Неравенство будет доказано (вместе со случаем равенства), если мы сможем показать, что минимум, на который распространяется ограничение , равно , а минимум достигается только тогда, когда . Сначала покажем, что задача условной минимизации имеет глобальный минимум.${\displaystyle \prod _{i=1}^{n}x_{i}=1}$${\displaystyle G(x_{1},x_{2},\ldots ,x_{n})=\prod _{i=1}^{n}x_{i}}$${\displaystyle F(x_{1},x_{2},\ldots ,x_{n})={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$${\displaystyle F(x_{1},x_{2},...,x_{n}),}$${\displaystyle G(x_{1},x_{2},\ldots ,x_{n})=1,}$${\displaystyle 1}$${\displaystyle x_{1}=x_{2}=\cdots =x_{n}=1}$

Установить . Поскольку пересечение компактно, теорема о крайнем значении гарантирует, что минимум из подчиняется ограничениям и достигается в некоторой точке внутри . С другой стороны, обратите внимание, что если любое из , then , while и . Это означает, что минимум внутри на самом деле является глобальным минимумом, поскольку значение в любой точке внутри определенно не меньше минимума, а значение в любой точке за пределами внутри строго больше, чем значение в , которое не меньше чем минимум.${\displaystyle K=\{(x_{1},x_{2},\ldots ,x_{n})\colon 0\leq x_{1},x_{2},\ldots ,x_{n}\leq n\}}$${\displaystyle K\cap \{G=1\}}$${\displaystyle F(x_{1},x_{2},...,x_{n})}$${\displaystyle G(x_{1},x_{2},\ldots ,x_{n})=1}$${\displaystyle (x_{1},x_{2},\ldots ,x_{n})\in K}$${\displaystyle K}$${\displaystyle x_{i}>n}$${\displaystyle F(x_{1},x_{2},\ldots ,x_{n})>1}$${\displaystyle F(1,1,\ldots ,1)=1}$${\displaystyle (1,1,\ldots ,1)\in K\cap \{G=1\}}$${\displaystyle K\cap \{G=1\}}$${\displaystyle F}$${\displaystyle K\cap \{G=1\}}$${\displaystyle F}$${\displaystyle (y_{1},y_{2},\ldots ,y_{n})}$${\displaystyle K}$${\displaystyle (1,1,\ldots ,1)}$

Метод множителей Лагранжа говорит , что глобальный минимум достигается в точке , где градиент является раз градиентом , для некоторых . Мы покажем, что это происходит только тогда, когда и ${\displaystyle (x_{1},x_{2},\ldots ,x_{n})}$${\displaystyle F(x_{1},x_{2},\ldots ,x_{n})}$${\displaystyle \lambda }$${\displaystyle G(x_{1},x_{2},\ldots ,x_{n})}$${\displaystyle \lambda }$${\displaystyle x_{1}=x_{2}=\cdots =x_{n}=1}$${\displaystyle F(x_{1},x_{2},...,x_{n})=1.}$

Вычислить и${\displaystyle {\frac {\partial F}{\partial x_{i}}}={\frac {1}{n}}}$

${\displaystyle {\frac {\partial G}{\partial x_{i}}}=\prod _{j\neq i}x_{j}={\frac {G(x_{1},x_{2},\ldots ,x_{n})}{x_{i}}}={\frac {1}{x_{i}}}}$

по ограничению. Таким образом, установка градиентов, пропорциональных друг другу, дает для каждого то и так. Поскольку левая часть не зависит от , из этого следует , и, поскольку , следует, что и , как желательно.${\displaystyle i}$${\displaystyle {\frac {1}{n}}={\frac {\lambda }{x_{i}}},}$${\displaystyle n\lambda =x_{i}.}$${\displaystyle i}$${\displaystyle x_{1}=x_{2}=\cdots =x_{n}}$${\displaystyle G(x_{1},x_{2},\ldots ,x_{n})=1}$${\displaystyle x_{1}=x_{2}=\cdots =x_{n}=1}$${\displaystyle F(x_{1},x_{2},\ldots ,x_{n})=1}$

Обобщения [ править ]

Взвешенное неравенство AM – GM [ править ]

Аналогичное неравенство существует для средневзвешенного арифметического и средневзвешенного геометрического . В частности, пусть неотрицательные числа x ₁ , x ₂ ,. . . , Х _п и неотрицательные веса W ₁ , W ₂ ,. . . , w _n быть дано. Положим w = w ₁ + w ₂ + · · · + w _n . Если  w > 0 , то неравенство

${\displaystyle {\frac {w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}}{w}}\geq {\sqrt[{w}]{x_{1}^{w_{1}}x_{2}^{w_{2}}\cdots x_{n}^{w_{n}}}}}$

выполняется с равенством тогда и только тогда, когда все x _k с w _k > 0 равны. Здесь используется соглашение 0 ⁰ = 1 .

Если все w _k = 1 , это сводится к приведенному выше неравенству среднего арифметического и геометрического.

Доказательство с использованием неравенства Дженсена [ править ]

Используя конечную форму неравенства Йенсена для натурального логарифма , мы можем доказать неравенство между взвешенным средним арифметическим и средневзвешенным геометрическим средним, указанное выше.

Поскольку x _k с весом w _k = 0 не влияет на неравенство, мы можем далее предполагать, что все веса положительны. Если все x _k равны, то равенство выполняется. Следовательно, остается доказать строгое неравенство, если не все они равны, что мы и будем предполагать в дальнейшем. Если хотя бы один x _k равен нулю (но не все), то средневзвешенное геометрическое среднее равно нулю, а средневзвешенное арифметическое положительно, следовательно, выполняется строгое неравенство. Следовательно, мы можем также считать, что все x _k положительны.

Поскольку натуральный логарифм строго вогнутый , конечная форма неравенства Йенсена и функциональных уравнений натурального логарифма подразумевает

${\displaystyle {\begin{aligned}\ln {\Bigl (}{\frac {w_{1}x_{1}+\cdots +w_{n}x_{n}}{w}}{\Bigr )}&>{\frac {w_{1}}{w}}\ln x_{1}+\cdots +{\frac {w_{n}}{w}}\ln x_{n}\\&=\ln {\sqrt[{w}]{x_{1}^{w_{1}}x_{2}^{w_{2}}\cdots x_{n}^{w_{n}}}}.\end{aligned}}}$

Поскольку натуральный логарифм строго возрастает ,

${\displaystyle {\frac {w_{1}x_{1}+\cdots +w_{n}x_{n}}{w}}>{\sqrt[{w}]{x_{1}^{w_{1}}x_{2}^{w_{2}}\cdots x_{n}^{w_{n}}}}.}$

Матричное арифметическое среднее геометрическое неравенство [ править ]

Большинство матричных обобщений неравенства среднего геометрического применяется на уровне унитарно инвариантных норм, поскольку даже если матрицы и являются положительно полуопределенными, матрица не может быть положительно полуопределенной и, следовательно, может не иметь канонического квадрата. корень. В ^[5] Бхатиа и Киттане доказали, что для любой унитарно инвариантной нормы и положительно полуопределенных матриц, и это так, что${\displaystyle A}$${\displaystyle B}$${\displaystyle AB}$${\displaystyle |||\cdot |||}$${\displaystyle A}$${\displaystyle B}$

${\displaystyle |||AB|||\leq {\frac {1}{2}}|||A^{2}+B^{2}|||}$

Позже в ^[6] те же авторы доказали более сильное неравенство

${\displaystyle |||AB|||\leq {\frac {1}{4}}|||(A+B)^{2}|||}$

Наконец, известно, что для размерности справедливо следующее сильнейшее матричное обобщение неравенства среднего арифметико-геометрического, и предполагается, что оно справедливо для всех${\displaystyle n=2}$${\displaystyle n}$

${\displaystyle |||(AB)^{\frac {1}{2}}|||\leq {\frac {1}{2}}|||A+B|||}$

Другие обобщения [ править ]

Другие обобщения неравенства средних арифметических и геометрических включают:

• Неравенство Мюрхеда ,
• Неравенство Маклорена ,
• Обобщенное среднее неравенство .

См. Также [ править ]

• Загадка упаковки Хоффмана
• Кай Фань неравенство
• Неравенство Юнга для продуктов

Примечания [ править ]

Новые неравенства с классическими средними появились в ряде публикаций (см. [7]).

Ссылки [ править ]

7. Флорин Ничита, О неравенстве классических средств, Энциклопедия научного сообщества, MDPI, https://encyclopedia.pub/2364 - Создано: 20 августа 2020 г .; Обновлено: 20 авг.2020 г.

Внешние ссылки [ править ]

• Артур Лохуотер (1982). «Введение в неравенство» . Электронная книга в формате PDF.