Бесконечная диэдральная группа

Эта статья требует дополнительных ссылок для проверки . Пожалуйста, помогите улучшить эту статью , добавив цитаты из надежных источников . Материал, не полученный от источника, может быть оспорен и удален.
Найти источники: «Бесконечная двугранная группа» - новости · газеты · книги · ученый · JSTOR ( июль 2011 г. ) ( Узнайте, как и когда удалить это сообщение-шаблон )

p1m1, ( * ∞∞ )	р2, (22∞)	p2mg, (2 * ∞)


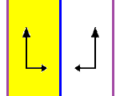В двумерном пространстве три группы фризов p1m1, p2 и p2mg изоморфны группе Dih _∞ . У всех есть 2 генератора. Первая имеет две параллельные линии отражения, вторая - два двукратных вращения, а последняя - одно зеркало и одно двукратное вращение.

В одном измерении бесконечная двугранная группа видна в симметрии апейрогона, чередующегося с двумя длинами ребер, содержащих точки отражения в центре каждого ребра.

В математике , то бесконечная группа диэдра DIH _∞ является бесконечная группа со свойствами , аналогичными свойствам конечных двугранных групп .

В двумерной геометрии , то бесконечная группа диэдра представляет собой группу фриз симметрию, p1m1 , рассматривается в качестве бесконечного множества параллельных отражений вдоль оси.

Определение [ править ]

Каждая группа диэдра порождается вращением r и отражением; если вращение является рациональным кратным полному вращению, то существует некоторое целое число n такое, что r ⁿ является единицей, и у нас есть конечная группа диэдра порядка 2 n . Если вращение не является рациональным кратным полному вращению, то такого n не существует, и результирующая группа имеет бесконечно много элементов и называется Dih _∞ . Есть презентации

{\ Displaystyle \ langle r, s \ mid s ^ {2} = 1, srs = r ^ {- 1} \ rangle \, \!}

\langle x,y\mid x^{2}=y^{2}=1\rangle \,\!

^[1]

и изоморфен полупрямое произведение из Z и Z / 2, а также к свободному произведению Z / 2 * Z / 2. Это группа автоморфизмов графа, состоящая из пути, бесконечного в обе стороны. Соответственно, это изометрическая группа из Z (смотрите также симметрии групп в одном измерении ), группу перестановки α: Z → Z , удовлетворяющий | i - j | = | & Alpha ; ( я ) - & alpha ; ( J ) |, для всех I, J в Z . ^[2]

Бесконечная группа диэдра также может быть определена как голоморфом из бесконечной циклической группы .

Псевдоним [ править ]

При периодической выборке синусоидальной функции с частотой

f s

, абсцисса выше представляет ее частоту, а ордината представляет другую синусоиду, которая может дать такой же набор выборок. Бесконечное число абсцисс имеет одну и ту же ординату (класс эквивалентности с фундаментальной областью

[0, f s / 2]

), и они демонстрируют диэдральную симметрию. Феномен "многие к одному" известен как наложение .

Примером бесконечной двугранной симметрии является наложение действительных сигналов.

При выборке функции с частотой $f s$ (интервалы $1 / f s$ ) следующие функции дают идентичные наборы выборок: ${sin (2π (f + Nf s) t + φ), N = 0, \pm 1, \pm 2, \pm 3, ...$ }. Таким образом, обнаруженное значение частоты $f$ является периодическим , что дает элемент трансляции $r = f s$ . Говорят, что функции и их частоты являются псевдонимами друг друга. Отмечая тригонометрическую идентичность:

\sin(2\pi (f+Nf_{s})t+\phi )=\left\{{\begin{array}{ll}+\sin(2\pi (f+Nf_{s})t+\phi ),&f+Nf_{s}\geq 0\\-\sin(2\pi |f+Nf_{s}|t-\phi ),&f+Nf_{s}<0\\\end{array}}\right.

мы можем записать все частоты псевдонимов как положительные значения: $| f + N f s |$ . Это дает элемент отражения ( $f$ ), а именно $f$ ↦ $- f$ . Например, при $f = 0,6 f s$ и $N = -1$ , $f + Nf s = -0,4 f s$ отражается до $0,4 f s$ , что приводит к двум крайним левым черным точкам на рисунке. ^{[примечание 1]} Две другие точки соответствуют $N = -2$ и $N = 1$ . Как показано на рисунке, существуют симметрии отражения при 0,5 $f s$ , $f s$ , 1,5 $f s$ и т. Д. Формально, частное при наложении спектров - это орбифолд [0, 0,5 $f s$ ] с действием Z / 2 на концах. (точки орбифолда), соответствующие отражению.

См. Также [ править ]

Ортогональная группа O (2), еще бесконечное обобщение конечных групп двугранных
Аффинная симметрическая группа , семейство групп , включая бесконечный диэдр

Заметки [ править ]

^ При обработке сигналов симметрия относительно оси $f s / 2$ известна как сворачивание , а ось известна как частота сворачивания .

Ссылки [ править ]

^ Коннолли, Фрэнсис; Дэвис, Джеймс (август 2004 г.). «Группы препятствий к перестройкам бесконечной диэдральной группы». Геометрия и топология . 8 (3): 1043–1078. arXiv : math / 0306054 . DOI : 10,2140 / gt.2004.8.1043 .
^ Минакси Бхаттачарджи, Дугалд Макферсон, Рёгнвальдур Г. Мёллер, Питер М. Нойман. Заметки о бесконечных группах перестановок, выпуск 1689. Springer, 1998. p. 38 . ISBN 978-3-540-64965-6

[3] При обработке сигналов симметрия относительно оси $f s / 2$ известна как сворачивание , а ось известна как частота сворачивания .

[1] Коннолли, Фрэнсис; Дэвис, Джеймс (август 2004 г.). «Группы препятствий к перестройкам бесконечной диэдральной группы». Геометрия и топология . 8 (3): 1043–1078. arXiv : math / 0306054 . DOI : 10,2140 / gt.2004.8.1043 .

[2] Минакси Бхаттачарджи, Дугалд Макферсон, Рёгнвальдур Г. Мёллер, Питер М. Нойман. Заметки о бесконечных группах перестановок, выпуск 1689. Springer, 1998. p. 38 . ISBN 978-3-540-64965-6

[1]