Эта статья требует дополнительных ссылок для проверки . ( октябрь 2009 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения ) |
В геометрии , А простой многоугольник / р ɒ л ɪ ɡ ɒ п / является многоугольник , который не пересекается сам по себе и не имеет отверстий. То есть это плоская форма, состоящая из прямых непересекающихся отрезков или «сторон», которые соединяются попарно для образования единой замкнутой траектории. Если стороны пересекаются, то многоугольник не простой. Квалификатор "простой" часто опускается, и тогда понимается, что приведенное выше определение определяет многоугольник в целом.
Приведенное выше определение обеспечивает следующие свойства:
- Многоугольник охватывает область (называемую его внутренней частью), у которой всегда есть измеримая площадь .
- Сегменты линии, составляющие многоугольник (называемые сторонами или ребрами), встречаются только в своих конечных точках, называемых вершинами (сингулярное: вершина) или менее формально «углами».
- В каждой вершине пересекаются ровно два ребра.
- Количество ребер всегда равно количеству вершин.
Два края, встречающиеся в углу, обычно требуются для образования непрямого угла (180 °); в противном случае коллинеарные отрезки линии будут считаться частями одной стороны.
Математики обычно используют «многоугольник» для обозначения только формы, образованной линейными сегментами, а не замкнутой области, однако некоторые могут использовать «многоугольник» для обозначения плоской фигуры, которая ограничена замкнутым путем, состоящим из конечной последовательности. отрезков прямых (т. е. замкнутой ломаной ). Согласно используемому определению, эта граница может или не может быть частью самого многоугольника. [1]
Простые многоугольники также называются многоугольниками Жордана , потому что теорема о кривой Жордана может быть использована для доказательства того, что такой многоугольник делит плоскость на две области: область внутри нее и область за ее пределами. Многоугольник на плоскости является простым тогда и только тогда , когда оно топологически эквивалентно к окружности . Его внутренность топологически эквивалентна диску .
Слабо простой многоугольник [ править ]
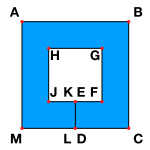
Если набор непересекающихся отрезков прямых образует границу области плоскости, которая топологически эквивалентна диску, то эта граница называется слабо простым многоугольником . [2] На изображении слева ABCDEFGHJKLM - это слабо простой многоугольник в соответствии с этим определением, с синим цветом отмечена область, для которой он является границей. Этот тип слабо простого многоугольника может возникнуть в компьютерной графике и САПР.как компьютерное представление многоугольных областей с отверстиями: для каждого отверстия создается «вырез», соединяющий его с внешней границей. Ссылаясь на изображение выше, ABCM - это внешняя граница плоской области с отверстием FGHJ. Разрез ED соединяет отверстие с внешней стороной и дважды пересекается в результирующем слабо простом многоугольном представлении.
В альтернативном и более общем определении слабо простых многоугольников они представляют собой пределы последовательностей простых многоугольников одного комбинаторного типа со сходимостью относительно расстояния Фреше . [3] Это формализует представление о том, что такой многоугольник позволяет сегментам касаться, но не пересекаться. Однако этот тип слабо простого многоугольника не обязательно должен формировать границу области, так как его «внутренность» может быть пустой. Например, обращаясь к изображению выше, многоугольная цепочка ABCBA является слабо простым многоугольником в соответствии с этим определением: ее можно рассматривать как предел «сжатия» многоугольника ABCFGHA.
Вычислительные проблемы [ править ]
В вычислительной геометрии несколько важных вычислительных задач включают входные данные в виде простого многоугольника; В каждой из этих проблем различие между внешним и внутренним имеет решающее значение при определении проблемы. [4]
- Точку в полигон испытаний включает в себя определение, для простого многоугольника P и точкой запроса д , является ли Q внутренней лжет P . [5]
- Известны простые формулы для вычисления площади многоугольника ; то есть площадь внутри многоугольника. [6]
- Разделение многоугольника - это набор примитивных единиц (например, квадратов), которые не перекрываются и объединение которых равно многоугольнику. Задача разбиения многоугольника - это проблема нахождения минимального в некотором смысле разбиения, например, разбиение с наименьшим числом единиц или с единицами наименьшей общей длины стороны. [7]
- Частным случаем разбиения многоугольника является триангуляция многоугольника : деление простого многоугольника на треугольники. Хотя выпуклые многоугольники легко триангулировать, триангулировать обычный простой многоугольник сложнее, потому что нам нужно избегать добавления ребер, пересекающихся за пределами многоугольника. Тем не менее, Бернар Шазель в 1991 году показал, что любой простой многоугольник с n вершинами можно триангулировать за Θ ( n ) время, что является оптимальным. Тот же алгоритм можно также использовать для определения того, образует ли замкнутая многоугольная цепочка простой многоугольник.
- Другой частный случай - это проблема художественной галереи , которую можно эквивалентно переформулировать как разбиение на минимальное количество звездообразных многоугольников . [7]
- Логические операции над многоугольниками : различные логические операции над наборами точек, заданными многоугольными областями.
- Выпуклая оболочка простого многоугольника может быть вычислена более эффективно , чем выпуклая оболочка других типов входов, такие как выпуклая оболочка множества точек.
- Диаграмма Вороного простого многоугольника
- Средняя ось / топологический каркас / прямой каркас простого многоугольника
- Кривая смещения простого многоугольника
- Сумма Минковского для простых многоугольников
Ссылки [ править ]
- ^ Grünbaum, B .; Выпуклые многогранники, 2-е изд., Springer, 2003
- ^ Думитреску, Адриан; Тот, Чаба Д. (2007). «Легкие ортогональные сети с постоянным геометрическим растяжением». В Томасе, Вольфганге; Вейль, Паскаль (ред.). STACS 2007: 24-й ежегодный симпозиум по теоретическим аспектам информатики, Ахен, Германия, 22-24 февраля 2007 г., Протоколы (иллюстрированное издание). Springer. п. 177. ISBN. 978-3540709176.
- ↑ Сянь-Чжи Чанг; Джефф Эриксон; Чао Сюй (2015). Труды Двадцать шестого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA'15) . С. 1655–1670.
- ^ Comp.graphics.algorithms FAQ ,котором перечислены решения математических задач с 2D и 3D многоугольников.
- ^ Хейнс, Эрик (1994). «Стратегии точки в многоугольнике» . В Хекберте, Пол С. (ред.). Самоцветы графики IV . Сан-Диего, Калифорния, США: Academic Press Professional, Inc., стр. 24–46 . ISBN 0-12-336155-9.
- ↑ Барт Брейден (1986). «Формула геодезической площади» (PDF) . Журнал математики колледжа . 17 (4): 326–337. DOI : 10.2307 / 2686282 . JSTOR 2686282 . Архивировано из оригинального (PDF) 07.11.2012.
- ^ а б Ли, DT (1998). «Глава 19: Вычислительная геометрия I». В Аталлах, Михаил Дж. (Ред.). Справочник по алгоритмам и теории вычислений . Серия Chapman & Hall / CRC «Прикладные алгоритмы и структуры данных». CRC Press. ISBN 9781420049503.См. «Другие разложения» с. 19-25 .
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Простой многоугольник» . MathWorld .