Теорема Зейферта – Ван Кампена.

В математике , то теорема Зайферт-Ван Кампна из алгебраической топологии ( по имени Герберта Зайферт и Эгберт ван Кампен ), иногда просто называется теоремой Ван Кампена , выражает структуру фундаментальной группы в виде топологического пространства в терминах фундаментальных групп двух открытых , линейно связные подпространства, покрывающие . Поэтому его можно использовать для вычислений фундаментальной группы пространств, построенных из более простых.${\ displaystyle X}$${\ displaystyle X}$

Теорема Ван Кампена для фундаментальных групп

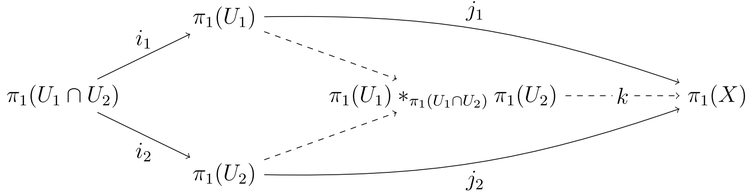
Пусть X - топологическое пространство, которое представляет собой объединение двух открытых и линейно связанных подпространств U ₁ , U ₂ . Предположим, что U ₁ ∩ U ₂ линейно связно и непусто, и пусть x ₀ - точка в U ₁ ∩ U _2, которая будет использоваться в качестве базы всех фундаментальных групп. Отображения включения U ₁ и U ₂ в X индуцируют гомоморфизмы групп и . Тогда X линейно связно и и${\ displaystyle j_ {1}: \ pi _ {1} (U_ {1}, x_ {0}) \ to \ pi _ {1} (X, x_ {0})}$${\ displaystyle j_ {2}: \ pi _ {1} (U_ {2}, x_ {0}) \ to \ pi _ {1} (X, x_ {0})}$${\ displaystyle j_ {1}}$${\ displaystyle j_ {2}}$сформировать коммутативную выталкивающую диаграмму:

Естественный морфизм k является изоморфизмом. То есть фундаментальная группа X является свободным произведением фундаментальных групп U ₁ и U ₂ с объединением . ^[1]${\ displaystyle \ pi _ {1} (U_ {1} \ cap U_ {2}, x_ {0})}$

Обычно морфизмы, индуцированные включением в эту теорему, сами по себе не инъективны, и более точная версия утверждения выражается в терминах выталкивания групп.

Теорема Ван Кампена для фундаментальных группоидов

К сожалению, приведенная выше теорема не вычисляет фундаментальную группу окружности, которая является наиболее важным базовым примером в алгебраической топологии. Причина в том, что круг не может быть реализован как объединение двух открытых множеств со связным пересечением. Эту проблему можно решить, работая с фундаментальным группоидом на множестве A базовых точек, выбранных в соответствии с геометрией ситуации. Таким образом, для круга используются две базовые точки. ^[2]${\ displaystyle \ pi _ {1} (X, A)}$

Это группоид состоит из гомотопических классов относительно конечных точек путей в Й присоединении точек A ∩ X . В частности, если X - стягиваемое пространство и A состоит из двух различных точек X , то легко видеть, что он изоморфен группоиду, который часто записывается с двумя вершинами и ровно одним морфизмом между любыми двумя вершинами. Этот группоид играет роль в теории группоидов, аналогичную роли группы целых чисел в теории групп. ^[3] Группоид также позволяет группоидам понятие гомотопии: это объект с единичным интервалом.${\ displaystyle \ pi _ {1} (X, A)}$${\displaystyle {\mathcal {I}}}$${\displaystyle {\mathcal {I}}}$ в категории группоидов.

Связное объединение двух несвязных пространств с множеством базовых точек

Категория группоидов допускает все копределы и, в частности, все выталкивания.

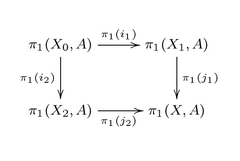
Теорема. Пусть топологическое пространство X покрывается внутренностей двух подпространств Х ₁ , Х ₂ , и пусть быть множество , которое удовлетворяет каждого пути компонент X ₁ , X ₂ и X ₀ = X ₁ ∩ X ₂ . Тогда A встречает каждую компоненту пути X и диаграмму P морфизмов, индуцированных включением

представляет собой выталкивающую диаграмму в категории группоидов. ^[4]

Эта теорема дает переход от топологии к алгебре, полностью определяя фундаментальный группоид ; затем нужно использовать алгебру и комбинаторику, чтобы определить фундаментальную группу в некоторой базовой точке.${\displaystyle \pi _{1}(X,A)}$

Одна из интерпретаций теоремы состоит в том, что она вычисляет гомотопические 1-типы. Чтобы увидеть его полезность, можно легко найти случаи, когда X соединен, но представляет собой объединение внутренних частей двух подпространств, каждое из которых имеет, скажем, 402 компонента пути и пересечение которых имеет, скажем, 1004 компонента пути. Интерпретация этой теоремы как вычислительного инструмента для «фундаментальных групп» требует некоторого развития «комбинаторной теории группоидов». ^{[5] [6]} Эта теорема подразумевает вычисление фундаментальной группы круга как группы целых чисел, поскольку группа целых чисел получается из группоида путем отождествления в категории группоидов двух его вершин.${\displaystyle {\mathcal {I}}}$

Существует версия последней теоремы, когда X покрывается объединением внутренностей семейства подмножеств. ^{[7] [8]}${\displaystyle \{U_{\lambda }:\lambda \in \Lambda \}}$

Вывод состоит в том, что если A встречает каждую компоненту пути всех 1,2,3-кратных пересечений множеств , то A встречает все компоненты пути X и диаграммы${\displaystyle U_{\lambda }}$

${\displaystyle \bigsqcup _{(\lambda ,\mu )\in \Lambda ^{2}}\pi _{1}(U_{\lambda }\cap U_{\mu },A)\rightrightarrows \bigsqcup _{\lambda \in \Lambda }\pi _{1}(U_{\lambda },A)\rightarrow \pi _{1}(X,A)}$

морфизмов, индуцированных включениями, является соуравнителем в категории группоидов.

[...] люди по-прежнему упорно упорствуют при расчетах с фундаментальными группами в фиксации единственной базовой точки вместо того, чтобы ловко выбирать весь пакет точек, который инвариантен относительно симметрии ситуации, которые, таким образом, теряются в пути. В определенных ситуациях (например, теоремы спуска для фундаментальных групп а-ля Ван Кампен) гораздо более элегантно, даже необходимо для понимания чего-либо, работать с фундаментальными группоидами относительно подходящего пакета базовых точек [...]

-  Александр Гротендик , программа Esquisse d'un (Раздел 2, английский перевод )

Эквивалентные составы

На языке комбинаторной теории групп if - топологическое пространство; и являются открытыми, линейно связанными подпространствами в ; непусто и линейно связно; и ; то есть свободное произведение с объединенной подгруппой из и , по отношению к (не обязательно инъективным) гомоморфизмам и . Данные групповые презентации :${\displaystyle X}$${\displaystyle U}$${\displaystyle V}$${\displaystyle X}$${\displaystyle U\cap V}$${\displaystyle w\in U\cap V}$${\displaystyle \pi _{1}(X,w)}$${\displaystyle \pi _{1}(U,w)}$${\displaystyle \pi _{1}(V,w)}$${\displaystyle I:\pi _{1}(U\cap V,w)\to \pi _{1}(U,w)}$${\displaystyle J:\pi _{1}(U\cap V,w)\to \pi _{1}(V,w)}$

${\displaystyle {\begin{aligned}\pi _{1}(U,w)&=\langle u_{1},\cdots ,u_{k}\mid \alpha _{1},\cdots ,\alpha _{l}\rangle \\\pi _{1}(V,w)&=\langle v_{1},\cdots ,v_{m}\mid \beta _{1},\cdots ,\beta _{n}\rangle \\\pi _{1}(U\cap V,w)&=\langle w_{1},\cdots ,w_{p}\mid \gamma _{1},\cdots ,\gamma _{q}\rangle \end{aligned}}}$

объединение можно представить ^[9] как

${\displaystyle \pi _{1}(X,w)=\left\langle u_{1},\cdots ,u_{k},v_{1},\cdots ,v_{m}\left|\alpha _{1},\cdots ,\alpha _{l},\beta _{1},\cdots ,\beta _{n},I(w_{1})J(w_{1})^{-1},\cdots ,I(w_{p})J(w_{p})^{-1}\right.\right\rangle .}$

В теории категорий , является Кодекартов Квадрат , в категории групп, диаграммы:${\displaystyle \pi _{1}(X,w)}$

${\displaystyle \pi _{1}(U,w)\gets \pi _{1}(U\cap V,w)\to \pi _{1}(V,w).}$

Примеры

2-сфера

Можно использовать теорему Ван Кампена для вычисления фундаментальных групп топологических пространств, которые можно разложить на более простые пространства. Например, рассмотрим сферу . Выберите открытые множества и где п и s обозначают северные и южные полюса соответственно. Тогда мы обладаем тем свойством, что A , B и A ∩ B являются множествами с открытой линейной связью. Таким образом, мы видим, что существует коммутативная диаграмма, включающая A ∩ B в A и B, а затем еще одно включение из A и B в${\displaystyle S^{2}}$${\displaystyle A=S^{2}\setminus \{n\}}$${\displaystyle B=S^{2}\setminus \{s\}}$${\displaystyle S^{2}}$и что существует соответствующая диаграмма гомоморфизмов между фундаментальными группами каждого подпространства. Применение теоремы Ван Кампена дает результат

${\displaystyle \pi _{1}(S^{2})=\pi _{1}(A)\cdot \pi _{1}(B)/\ker(\Phi ).}$

Однако A и B оба гомеоморфны R ^2, который односвязен, поэтому и A, и B имеют тривиальные фундаментальные группы. Отсюда ясно, что фундаментальная группа группы тривиальна.${\displaystyle S^{2}}$

Сумма пробелов клина

Учитывая два заостренных пространство и мы можем сформировать их клиновидную сумму , путь профакторизовав путем определения их два базисных точек.${\displaystyle (X,x)}$${\displaystyle (Y,y)}$${\displaystyle (X\vee Y,p)}$${\displaystyle X\coprod Y}$

Если допускает стягиваемую открытую окрестность и стягиваемую открытую окрестность (что имеет место, например, если, например, и являются CW-комплексами ), то мы можем применить теорему Ван Кампена к , взяв и в качестве двух открытых множеств, и мы заключаем, что фундаментальная группа клина - это свободное произведение фундаментальных групп двух пространств, с которых мы начали:${\displaystyle x}$${\displaystyle U\subset X}$${\displaystyle y}$${\displaystyle V\subset Y}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle X\vee Y}$${\displaystyle X\vee V}$${\displaystyle U\vee Y}$

${\displaystyle \pi _{1}(X\vee Y,p)\cong \pi _{1}(X,x)*\pi _{1}(Y,y)}$.

Ориентируемые поверхности рода g

Более сложным примером является вычисление фундаментальной группы ориентируемой поверхности S рода n , иначе известной как поверхностная группа рода n . Можно построить S, используя его стандартный фундаментальный многоугольник . Для первого открытого набора A выберите диск в центре многоугольника. Pick B , чтобы быть дополнением в S центральной точки A . Тогда пересечение A и B является кольцом, которое, как известно, гомотопически эквивалентно окружности (и поэтому имеет ту же фундаментальную группу). потом${\displaystyle \pi _{1}(A\cap B)=\pi _{1}(S^{1})}$, то есть целые числа, и . Таким образом, включение into переводит любой генератор в тривиальный элемент. Однако включение into нетривиально. Чтобы понять это, сначала нужно посчитать . Это легко сделать, так как можно деформировать ретракт B (который представляет собой S с удаленной одной точкой) на ребра, помеченные${\displaystyle \pi _{1}(A)=\pi _{1}(D^{2})={1}}$${\displaystyle \pi _{1}(A\cap B)}$${\displaystyle \pi _{1}(A)}$${\displaystyle \pi _{1}(A\cap B)}$${\displaystyle \pi _{1}(B)}$${\displaystyle \pi _{1}(B)}$

${\displaystyle A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}A_{2}^{-1}B_{2}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}.}$

Это пространство, как известно, представляет собой сумму клина из 2 n окружностей (также называемую букетом окружностей ), фундаментальная группа которой, как известно, изоморфна свободной группе с 2 n образующими, которые в этом случае могут быть представлены ребрами сами: . Теперь у нас достаточно информации, чтобы применить теорему Ван Кампена. Генераторы - это петли ( A односвязна, поэтому она не вносит никаких генераторов), и существует ровно одно отношение:${\displaystyle \{A_{1},B_{1},\cdots ,A_{n},B_{n}\}}$${\displaystyle \{A_{1},B_{1},\cdots ,A_{n},B_{n}\}}$

${\displaystyle A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}A_{2}B_{2}A_{2}^{-1}B_{2}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}=1.}$

Используя образующие и соотношения, эта группа обозначается

${\displaystyle \left\langle A_{1},B_{1},\cdots ,A_{n},B_{n}\left|A_{1}B_{1}A_{1}^{-1}B_{1}^{-1}\cdots A_{n}B_{n}A_{n}^{-1}B_{n}^{-1}\right.\right\rangle .}$

Простая связность

Если X - пространство, которое можно записать как объединение двух открытых односвязных множеств U и V, где U ∩ V непусто и линейно связно , то X односвязно. ^[10]

Обобщения

Как объяснялось выше, эта теорема была распространена Рональдом Брауном на несвязный случай с использованием фундаментального группоида на множестве A базовых точек. Теорема для произвольных покрытий с ограничением, что A пересекает все трехмерные пересечения множеств покрытия, приведена в статье Брауна и Абдула Разака Саллеха. ^[11] Теорема и доказательство для фундаментальной группы, но с использованием некоторых группоидных методов, также приведены в книге Дж. Питера Мэя . ^[12] Версия , которая позволяет более двух перекрывающихся наборов , но с A одноэлементно также приводится в Аллен Хэтчер книге «s ниже, теорема 1.20.${\displaystyle \pi _{1}(X,A)}$

Приложения фундаментального группоида на множестве базовых точек к теореме Жордана о кривой , покрывающим пространствам и пространствам орбит приведены в книге Рональда Брауна. ^[13] В случае пространств орбит удобно брать A, чтобы включить все неподвижные точки действия. Примером может служить действие сопряжения на круге.

Ссылки на многомерные версии теоремы, которые дают некоторую информацию о гомотопических типах, даны в статье о многомерных теориях групп и группоидах. ^[14] Таким образом, двумерная теорема Ван Кампена, которая вычисляет неабелевы вторые относительные гомотопические группы, была дана Рональдом Брауном и Филипом Дж. Хиггинсом. ^[15] Полный отчет и расширения на все измерения даны Брауном, Хиггинсом и Рафаэлем Сиверой, ^{[16], в} то время как расширение на n -кубы пространств дано Рональдом Брауном и Жан-Луи Лоде . ^[17]

Фундаментальные группы также появляются в алгебраической геометрии и являются основной темой первой Séminaire de géométrie algébrique Александра Гротендика (SGA1). Там появляется версия теоремы Ван Кампена, которая доказывается совершенно иным путем, чем в алгебраической топологии, а именно теорией спуска. Аналогичное доказательство работает в алгебраической топологии. ^[18]

Смотрите также

• Многомерная алгебра
• Теория высших категорий
• Псевдокружность
• Рональд Браун (математик)

Примечания

использованная литература

• Аллен Хэтчер, Алгебраическая топология. (2002) Cambridge University Press, Кембридж, xii + 544 стр. ISBN 0-521-79160-X и ISBN 0-521-79540-0  
• Питер Мэй, Краткий курс алгебраической топологии. (1999) University of Chicago Press, ISBN 0-226-51183-9 (раздел 2.7 дает теоретико-категориальное представление теоремы как копредел в категории группоидов) . 
• Рональд Браун, Группоиды и теорема Ван Кампена, Proc. Лондонская математика. Soc . (3) 17 (1967) 385–401.
• Обсуждение Mathoverflow по многим базовым моментам
• Рональд Браун, Топология и группоиды (2006) Booksurge LLC ISBN 1-4196-2722-8 
• Р. Браун и А. Разак, Теорема Ван Кампена для объединения несвязных пространств, Архив. Математика. 42 (1984) 85–88. (В этой статье дается, вероятно, оптимальная версия теоремы, а именно группоидная версия теоремы для произвольного открытого покрытия и набора базовых точек, которые пересекают каждую компоненту пути каждого 1-2-3-кратного пересечения множеств крышка.)
• П. Дж. Хиггинс, Категории и группоиды (1971), Ван Ностранд Рейнхольд
• Рональд Браун, Теория многомерных групп (2007) (дает широкий взгляд на многомерные теоремы Ван Кампена, включающие множественные группоиды) .
• Гринберг, Марвин Дж .; Харпер, Джон Р. (1981), Алгебраическая топология. Первый курс , Серия лекций по математике, 58 , Бенджамин / Каммингс, ISBN 0805335579
• Зайферт, Х. , Конструкция drei sizesaler geschlossener Raume . Berichte Sachs. Акад. Лейпциг, Math.-Phys. Kl. (83) (1931) 26–66.
• ER van Kampen. О связи между фундаментальными группами некоторых родственных пространств. Американский журнал математики, вып. 55 (1933), стр. 261–267.
• Браун Р., Хиггинс П. Дж. О связи между вторыми относительными гомотопическими группами некоторых родственных пространств , Proc. Лондонская математика. Soc. (3) 36 (1978) 193–212.
• Браун Р., Хиггинс П. Дж. И Сивера Р. 2011, EMS Tracts in Mathematics Vol.15 (2011) Неабелева алгебраическая топология: фильтрованные пространства, скрещенные комплексы, кубические гомотопические группоиды ; (В первой из трех частей обсуждаются приложения 1- и 2-мерной версии теоремы Зейферта – ван Кампена. Последняя позволяет вычислять неабелевы вторые относительные гомотопические группы и, фактически, гомотопические 2-типы. Вторая часть применяется теорема Ван Кампена о высшей гомотопии для скрещенных комплексов, доказанная в части III.)
• "Результат теоремы Ван Кампена" . PlanetMath .
• Р. Браун, Х. Кампс, Т. Портер: Гомотопический двойной группоид хаусдорфового пространства II: теорема Ван Кампена », Теория и приложения категорий, 14 (2005) 200–220.
• Дилан Г. Л. Аллегретти, Симплициальные множества и теорема Ван Кампена (обсуждаются обобщенные версии теоремы Ван Кампена, примененные к топологическим пространствам и симплициальным множествам).
• Р. Браун и Ж.-Л. Лодей, "Теоремы Ван Кампена для диаграмм пространств", Топология 26 (1987) 311–334.

Эта статья включает материал из теоремы Ван Кампена о PlanetMath , которая находится под лицензией Creative Commons Attribution / Share-Alike License .

внешняя ссылка

• СМИ, связанные с теоремой Зейферта – Ван Кампена на Викискладе?