Треугольник Паскаля

В математике треугольник Паскаля представляет собой треугольный массив биномиальных коэффициентов , который возникает в теории вероятностей, комбинаторике и алгебре. В большей части западного мира он назван в честь французского математика Блеза Паскаля , хотя другие математики изучали его за столетия до него в Индии, ^[1] Персии, ^[2] Китае, Германии и Италии. ^[3]

Строки треугольника Паскаля условно нумеруются, начиная с верхней строки (0-й строки). Записи в каждой строке нумеруются слева направо и обычно располагаются в шахматном порядке относительно номеров в соседних строках. Треугольник может быть построен следующим образом: в строке 0 (самая верхняя строка) есть уникальная ненулевая запись 1. Каждая запись каждой последующей строки строится путем добавления числа выше и левее с числом выше и ниже. справа, рассматривая пустые записи как 0. Например, начальное число в первой (или любой другой) строке равно 1 (сумма 0 и 1), тогда как числа 1 и 3 в третьей строке добавляются для получения номер 4 в четвертом ряду.${\ Displaystyle п = 0}$${\ Displaystyle к = 0}$

Запись в й строке и м столбце треугольника Паскаля обозначается . Например, уникальная ненулевая запись в самой верхней строке — это . В этих обозначениях конструкцию предыдущего абзаца можно записать следующим образом:${\ Displaystyle п}$${\ Displaystyle к}$${\ Displaystyle {п \ выберите к}}$${\ Displaystyle {0 \ выберите 0} = 1}$

для любого неотрицательного целого числа и любого целого числа . ^[4] Это повторение биномиальных коэффициентов известно как правило Паскаля .${\ Displaystyle п}$${\ Displaystyle 0 \ Leq к \ Leq п}$

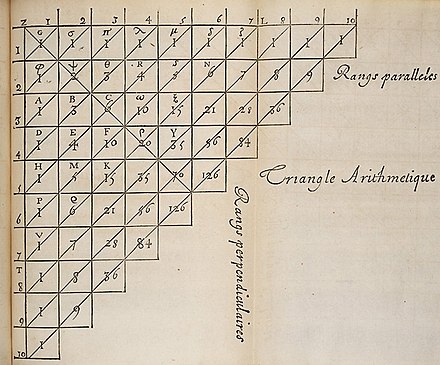
Схема чисел, образующих треугольник Паскаля, была известна задолго до самого Паскаля. Паскаль ввел новшество во многие ранее не засвидетельствованные способы использования чисел треугольника, которые он подробно описал в самом раннем известном математическом трактате , специально посвященном треугольнику, в его « Трактате арифметики треугольника» (1654 г.; опубликовано в 1665 г.).

${\displaystyle {\begin{array}{c}1\\1\quad 1\\1\quad 2\quad 1\\1\quad 3\quad 3\quad 1\\1\quad 4\quad 6\quad 4\quad 1\\1\quad 5\quad 10\quad 10\quad 5\quad 1\\1\quad 6\quad 15\quad 20\quad 15\quad 6\quad 1\\1\quad 7\quad 21\quad 35\quad 35\quad 21\quad 7\quad 1\\\end{array}}}$

Диаграмма, показывающая первые восемь рядов треугольника Паскаля.

В треугольнике Паскаля каждое число равно сумме двух чисел непосредственно над ним.

मेरु प्रस्तार (Меру Прастаара), используемый в индийских рукописях, получен из формул Пингалы . Рукопись из библиотеки Рагхунатх J&K; 755 г. н.э.

Треугольник Ян Хуэя , изображенный китайцами с помощью стержневых цифр , появляется в математическом труде Чжу Шицзе , датированном 1303 годом. Название гласит: «Старая методическая схема семи умножающих квадратов» (китайский: 古法七乘方圖). ; четвертый символ 椉 в названии изображения является архаичным).

Версия треугольника Паскаля

Визуализация биномиального разложения до 4-й степени

${\displaystyle {\begin{array}{c}{\binom {0}{0}}\\{\binom {1}{0}}\quad {\binom {1}{1}}\\{\binom {2}{0}}\quad {\binom {2}{1}}\quad {\binom {2}{2}}\\{\binom {3}{0}}\quad {\binom {3}{1}}\quad {\binom {3}{2}}\quad {\binom {3}{3}}\\{\binom {4}{0}}\quad {\binom {4}{1}}\quad {\binom {4}{2}}\quad {\binom {4}{3}}\quad {\binom {4}{4}}\\{\binom {5}{0}}\quad {\binom {5}{1}}\quad {\binom {5}{2}}\quad {\binom {5}{3}}\quad {\binom {5}{4}}\quad {\binom {5}{5}}\end{array}}}$

Шестистрочный треугольник Паскаля как биномиальные коэффициенты

Каждый кадр представляет собой строку в треугольнике Паскаля. Каждый столбец пикселей представляет собой двоичное число с младшим значащим битом внизу. Светлые пиксели представляют единицы, а темные пиксели — нули.

Количество композиций n + 1  на k  + 1 упорядоченных разбиений образует треугольник Паскаля.

Вывод симплексных чисел из выровненного слева треугольника Паскаля

Последовательность Фибоначчи в треугольнике Паскаля

Аппроксимация уровня 4 треугольника Серпинского, полученная путем закрашивания первых 32 строк треугольника Паскаля белым цветом, если биномиальный коэффициент четный, и черным, если он нечетный.

			10
		10	20

Треугольник Паскаля, наложенный на сетку, дает количество различных путей к каждому квадрату, при условии, что учитываются только движения вправо и вниз.

${\displaystyle {\begin{aligned}\exp {\begin{pmatrix}.&.&.&.&.\\1&.&.&.&.\\.&2&.&.&.\\.&.&3&.&.\\.&.&.&4&.\end{pmatrix}}&={\begin{pmatrix}1&.&.&.&.\\1&1&.&.&.\\1&2&1&.&.\\1&3&3&1&.\\1&4&6&4&1\end{pmatrix}}\\e^{\text{counting}}&={\text{binomial}}\end{aligned}}}$

Биномиальная матрица как матричная экспонента. Все точки представляют 0.

Биномиальные коэффициенты C  ( n , k ) , расширенные для отрицательных и дробных n , проиллюстрированы простым биномом . Можно заметить, что треугольник Паскаля повернут, а альтернативные члены отрицаются. Случай n  = −1 дает ряд Гранди .