Трилинейная интерполяция

Трилинейная интерполяция - это метод многомерной интерполяции на трехмерной регулярной сетке . Он аппроксимирует значение функции в промежуточной точке внутри локальной осевой прямоугольной призмы линейно, используя данные функции в точках решетки. Для произвольной неструктурированной сетки (используемой в анализе методом конечных элементов ) должны использоваться другие методы интерполяции; если все элементы сетки являются тетраэдрами (трехмерными симплексами ), то барицентрические координаты обеспечивают простую процедуру.${\ Displaystyle (х, у, г)}$

Трилинейная интерполяция часто используется в численном анализе , анализе данных и компьютерной графике .

По сравнению с линейной и билинейной интерполяцией [ править ]

Трилинейная интерполяция - это расширение линейной интерполяции , которая работает в пространствах с размерностью , и билинейной интерполяции , которая работает с размерностью , до измерения . Все эти схемы интерполяции используют полиномы 1-го порядка, что дает точность порядка 2, и для этого требуются смежные заранее определенные значения, окружающие точку интерполяции. Существует несколько способов получения трилинейной интерполяции, которая эквивалентна 3-мерной тензорной B-сплайн- интерполяции порядка 1, а оператор трилинейной интерполяции также является тензорным произведением 3-х линейных операторов интерполяции.${\ displaystyle D = 1}$${\ displaystyle D = 2}$${\ displaystyle D = 3}$${\ displaystyle 2 ^ {D} = 8}$

Метод [ править ]

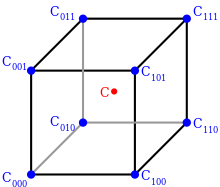
Восемь угловых точек на кубе, окружающем точку интерполяции C

Изображение трехмерной интерполяции

Геометрическая визуализация трилинейной интерполяции. Произведение значения в желаемой точке и всего объема равно сумме произведений значения в каждом углу и частичного объема по диагонали напротив угла.

На периодическую и кубической решетке, пусть , и быть различие между каждым из , , и меньше координат , связанный, то есть:${\ displaystyle x _ {\ text {d}}}$${\ displaystyle y _ {\ text {d}}}$${\ displaystyle z _ {\ text {d}}}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$

${\ displaystyle {\ begin {align} x _ {\ text {d}} = {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \\ y _ {\ text {d} } = {\ frac {y-y_ {0}} {y_ {1} -y_ {0}}} \\ z _ {\ text {d}} = {\ frac {z-z_ {0}} {z_ { 1} -z_ {0}}} \ конец {выровнено}}}$

где указывает точку решетки внизу и указывает точку решетки выше и аналогично для и .${\ displaystyle x_ {0}}$${\ displaystyle x}$${\ displaystyle x_ {1}}$${\ displaystyle x}$${\ displaystyle y_ {0}, y_ {1}, z_ {0}}$${\ displaystyle z_ {1}}$

Сначала мы выполняем интерполяцию (представьте, что мы «подталкиваем» грань куба, определяемую с помощью, к противоположной грани, определенной с помощью ), получая:${\ displaystyle x}$${\ displaystyle C_ {0jk}}$${\ displaystyle C_ {1jk}}$

${\displaystyle {\begin{aligned}c_{00}&=c_{000}(1-x_{\text{d}})+c_{100}x_{\text{d}}\\c_{01}&=c_{001}(1-x_{\text{d}})+c_{101}x_{\text{d}}\\c_{10}&=c_{010}(1-x_{\text{d}})+c_{110}x_{\text{d}}\\c_{11}&=c_{011}(1-x_{\text{d}})+c_{111}x_{\text{d}}\end{aligned}}}$

Где означает значение функции. Затем мы интерполируем эти значения ( "проталкивая" от до ), давая:${\displaystyle c_{000}}$${\displaystyle (x_{0},y_{0},z_{0}).}$${\displaystyle y}$${\displaystyle C_{i0k}}$${\displaystyle C_{i1k}}$

${\displaystyle {\begin{aligned}c_{0}&=c_{00}(1-y_{\text{d}})+c_{10}y_{\text{d}}\\c_{1}&=c_{01}(1-y_{\text{d}})+c_{11}y_{\text{d}}\end{aligned}}}$

Наконец, мы интерполируем эти значения (проходя по линии):${\displaystyle z}$

${\displaystyle c=c_{0}(1-z_{\text{d}})+c_{1}z_{\text{d}}.}$

Это дает нам прогнозируемое значение для точки.

Результат трилинейной интерполяции не зависит от порядка шагов интерполяции по трем осям: любой другой порядок, например, вдоль , затем вдоль и, наконец, вдоль , дает то же значение.${\displaystyle x}$${\displaystyle y}$${\displaystyle z}$

Вышеупомянутые операции можно визуализировать следующим образом: Сначала мы находим восемь углов куба, которые окружают нашу точку интереса. Эти углы имеют значения , , , , , , , .${\displaystyle c_{000}}$${\displaystyle c_{100}}$${\displaystyle c_{010}}$${\displaystyle c_{110}}$${\displaystyle c_{001}}$${\displaystyle c_{101}}$${\displaystyle c_{011}}$${\displaystyle c_{111}}$

Затем мы выполняем линейную интерполяцию между и, чтобы найти , и чтобы найти , и чтобы найти , и чтобы найти .${\displaystyle c_{000}}$${\displaystyle c_{100}}$${\displaystyle c_{00}}$${\displaystyle c_{001}}$${\displaystyle c_{101}}$${\displaystyle c_{01}}$${\displaystyle c_{011}}$${\displaystyle c_{111}}$${\displaystyle c_{11}}$${\displaystyle c_{010}}$${\displaystyle c_{110}}$${\displaystyle c_{10}}$

Теперь делаем интерполяцию между и чтобы найти , и чтобы найти . Наконец, мы вычисляем значение с помощью линейной интерполяции и${\displaystyle c_{00}}$${\displaystyle c_{10}}$${\displaystyle c_{0}}$${\displaystyle c_{01}}$${\displaystyle c_{11}}$${\displaystyle c_{1}}$${\displaystyle c}$${\displaystyle c_{0}}$${\displaystyle c_{1}}$

На практике трилинейная интерполяция идентична двух билинейной интерполяции в сочетании с линейной интерполяцией:

${\displaystyle c\approx l\left(b(c_{000},c_{010},c_{100},c_{110}),\,b(c_{001},c_{011},c_{101},c_{111})\right)}$

Альтернативный алгоритм [ править ]

Альтернативный способ написать решение задачи интерполяции:

${\displaystyle f(x,y,z)\approx a_{0}+a_{1}x+a_{2}y+a_{3}z+a_{4}xy+a_{5}xz+a_{6}yz+a_{7}xyz}$

где коэффициенты находятся из решения линейной системы

${\displaystyle {\begin{aligned}{\begin{bmatrix}1&x_{0}&y_{0}&z_{0}&x_{0}y_{0}&x_{0}z_{0}&y_{0}z_{0}&x_{0}y_{0}z_{0}\\1&x_{1}&y_{0}&z_{0}&x_{1}y_{0}&x_{1}z_{0}&y_{0}z_{0}&x_{1}y_{0}z_{0}\\1&x_{0}&y_{1}&z_{0}&x_{0}y_{1}&x_{0}z_{0}&y_{1}z_{0}&x_{0}y_{1}z_{0}\\1&x_{1}&y_{1}&z_{0}&x_{1}y_{1}&x_{1}z_{0}&y_{1}z_{0}&x_{1}y_{1}z_{0}\\1&x_{0}&y_{0}&z_{1}&x_{0}y_{0}&x_{0}z_{1}&y_{0}z_{1}&x_{0}y_{0}z_{1}\\1&x_{1}&y_{0}&z_{1}&x_{1}y_{0}&x_{1}z_{1}&y_{0}z_{1}&x_{1}y_{0}z_{1}\\1&x_{0}&y_{1}&z_{1}&x_{0}y_{1}&x_{0}z_{1}&y_{1}z_{1}&x_{0}y_{1}z_{1}\\1&x_{1}&y_{1}&z_{1}&x_{1}y_{1}&x_{1}z_{1}&y_{1}z_{1}&x_{1}y_{1}z_{1}\end{bmatrix}}{\begin{bmatrix}a_{0}\\a_{1}\\a_{2}\\a_{3}\\a_{4}\\a_{5}\\a_{6}\\a_{7}\end{bmatrix}}={\begin{bmatrix}c_{000}\\c_{100}\\c_{010}\\c_{110}\\c_{001}\\c_{101}\\c_{011}\\c_{111}\end{bmatrix}},\end{aligned}}}$

дающий результат

${\displaystyle {\begin{aligned}a_{0}={}&{\frac {-c_{000}x_{1}y_{1}z_{1}+c_{001}x_{1}y_{1}z_{0}+c_{010}x_{1}y_{0}z_{1}-c_{011}x_{1}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {c_{100}x_{0}y_{1}z_{1}-c_{101}x_{0}y_{1}z_{0}-c_{110}x_{0}y_{0}z_{1}+c_{111}x_{0}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{1}={}&{\frac {c_{000}y_{1}z_{1}-c_{001}y_{1}z_{0}-c_{010}y_{0}z_{1}+c_{011}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}y_{1}z_{1}+c_{101}y_{1}z_{0}+c_{110}y_{0}z_{1}-c_{111}y_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{2}={}&{\frac {c_{000}x_{1}z_{1}-c_{001}x_{1}z_{0}-c_{010}x_{1}z_{1}+c_{011}x_{1}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}x_{0}z_{1}+c_{101}x_{0}z_{0}+c_{110}x_{0}z_{1}-c_{111}x_{0}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{3}={}&{\frac {c_{000}x_{1}y_{1}-c_{001}x_{1}y_{1}-c_{010}x_{1}y_{0}+c_{011}x_{1}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}+{}\\&{\frac {-c_{100}x_{0}y_{1}+c_{101}x_{0}y_{1}+c_{110}x_{0}y_{0}-c_{111}x_{0}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{4}={}&{\frac {-c_{000}z_{1}+c_{001}z_{0}+c_{010}z_{1}-c_{011}z_{0}+c_{100}z_{1}-c_{101}z_{0}-c_{110}z_{1}+c_{111}z_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{5}=&{\frac {-c_{000}y_{1}+c_{001}y_{1}+c_{010}y_{0}-c_{011}y_{0}+c_{100}y_{1}-c_{101}y_{1}-c_{110}y_{0}+c_{111}y_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{6}={}&{\frac {-c_{000}x_{1}+c_{001}x_{1}+c_{010}x_{1}-c_{011}x_{1}+c_{100}x_{0}-c_{101}x_{0}-c_{110}x_{0}+c_{111}x_{0}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}},\\[4pt]a_{7}={}&{\frac {c_{000}-c_{001}-c_{010}+c_{011}-c_{100}+c_{101}+c_{110}-c_{111}}{(x_{0}-x_{1})(y_{0}-y_{1})(z_{0}-z_{1})}}.\end{aligned}}}$

См. Также [ править ]

• Линейная интерполяция
• Билинейная интерполяция
• Трикубическая интерполяция
• Радиальная интерполяция
• Тетраэдрическая интерполяция

Внешние ссылки [ править ]

• псевдокод от НАСА , описывает итеративную обратную трилинейную интерполяцию (учитывая вершины и значение C найти Xd, Yd и Zd).
• Пол Бурк, Методы интерполяции , 1999. Содержит очень умный и простой метод поиска трилинейной интерполяции, основанный на двоичной логике и который может быть расширен до любого измерения (тетралинейной, пенталинейной, ...).
• Кенрайт, Деформация тетраэдра произвольной формы. Международный симпозиум по визуальным вычислениям. Springer International Publishing, 2015 [1] .