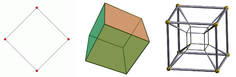

- Две точки можно соединить для создания отрезка линии .
- Два параллельных отрезка можно соединить в квадрат .
- Два параллельных квадрата можно соединить в куб .
- Два параллельных куба можно соединить в тессеракт .
| Геометрия |
|---|
 |
| Геометры |
В физике и математике , то размерность из математического пространства (или объекта) неформально определяется как минимальное количество координат , необходимых для определения любой точки внутри него. [1] [2] Таким образом, линия имеет размерность 1 (1D), потому что для определения точки на ней требуется только одна координата - например, точка 5 на числовой прямой. Поверхности , такие как плоскость или поверхность цилиндра или сферы имеет размерность два(2D), потому что для определения точки на нем необходимы две координаты - например, широта и долгота необходимы для определения местоположения точки на поверхности сферы. Внутренняя часть куба , цилиндра или сферы является трехмерной (3D), потому что для определения точки в этих пространствах необходимы три координаты.
В классической механике , пространство и время являются различными категориями и относится к абсолютному пространству и времени . Эта концепция мира представляет собой четырехмерное пространство, но не то, которое было сочтено необходимым для описания электромагнетизма . Четыре измерения (4D) пространства-времени состоят из событий , которые не являются абсолютно определенными в пространстве и времени, а скорее известны относительно движения наблюдателя . Пространство Минковского сначала приближает Вселенную без гравитации ; то псевдоримановы многообразия из ОТОописывать пространство-время с помощью материи и гравитации. 10 измерений используются для описания теории суперструн (6D гиперпространство + 4D), 11 измерений могут описывать супергравитацию и M-теорию (7D гиперпространство + 4D), а пространство состояний квантовой механики является бесконечномерным функциональным пространством .
Концепция измерения не ограничивается физическими объектами. Высокое-мерное пространство ы часто возникают вматематики и науки. Они могут быть пространствами параметров или конфигурационными пространствами, такими как в лагранжевой или гамильтоновой механике ; это абстрактные пространства , независимые от физического пространства, в котором мы живем.
По математике [ править ]
В математике размер объекта - это, грубо говоря, количество степеней свободы точки, которая движется на этом объекте. Другими словами, размер - это количество независимых параметров или координат , которые необходимы для определения положения точки, которая должна находиться на объекте. Например, размер точки равен нулю; размер линии равен единице, поскольку точка может перемещаться по линии только в одном направлении (или его противоположном); размер плоскости - два и т. д.
Размерность - это внутреннее свойство объекта, в том смысле, что оно не зависит от измерения пространства, в которое объект находится или может быть встроен. Например, кривая , такая как круг , имеет размер один, потому что положение точки на кривой определяется расстоянием со знаком вдоль кривой до фиксированной точки на кривой. Это не зависит от того факта, что кривая не может быть вложена в евклидово пространство размерности меньше двух, если это не линия.
Размерность евклидова n -пространства E n равна n . При попытке обобщения на другие типы пространств возникает вопрос «что делает E n n -мерным?» Один ответ состоит в том, что для покрытия неподвижного шара в E n маленькими шарами радиуса ε требуется порядка ε - n таких маленьких шариков. Это наблюдение приводит к определению размерности Минковского и ее более сложного варианта - размерности Хаусдорфа., но есть и другие ответы на этот вопрос. Например, граница шара в E n выглядит локально как E n -1, и это приводит к понятию индуктивного измерения . Хотя эти понятия согласуются с E n , они оказываются разными, если смотреть на более общие пространства.
Тессеракт является примером четырехмерного объекта. В то время как вне математики термин «измерение» используется как «тессеракт имеет четыре измерения », математики обычно выражают это как: «тессеракт имеет размерность 4 » или: «размер тессеракта равен 4» или: 4D.
Хотя понятие высших измерений восходит к Рене Декарту , существенное развитие геометрии более высоких измерений началось только в 19 веке благодаря работам Артура Кейли , Уильяма Роуэна Гамильтона , Людвига Шлефли и Бернхарда Римана . Риман 1854 Habilitationsschrift , Шлефло 1 852 Теорье дер vielfachen Kontinuität , и обнаружение Гамильтон из кватернионов и Джона Т. Грейвса открытие "из октонионов в 1843 году положили начало многомерной геометрии.
В оставшейся части этого раздела рассматриваются некоторые из наиболее важных математических определений измерения.
Векторные пространства [ править ]
Размерность векторного пространства - это количество векторов в любом базисе пространства, то есть количество координат, необходимых для задания любого вектора. Это понятие размерности ( мощности базиса) часто называют размерностью Гамеля или алгебраической размерностью, чтобы отличить его от других понятий размерности.
Для несвободного случая это обобщается на понятие длины модуля .
Манифольды [ править ]
Можно вычислить однозначно определенную размерность каждого связного топологического многообразия . Связное топологическое многообразие локально гомеоморфно евклидову n -мерному пространству, в котором число n является размерностью многообразия.
Для связных дифференцируемых многообразий размерность также является размерностью касательного векторного пространства в любой точке.
В геометрической топологии теория многообразий характеризуется тем, что измерения 1 и 2 относительно элементарны, многомерные случаи n > 4 упрощаются за счет наличия дополнительного пространства для «работы»; и случаи n = 3 и 4 в некотором смысле являются наиболее трудными. Такое положение дел было очень заметно в различных случаях гипотезы Пуанкаре , где применяются четыре различных метода доказательства.
Сложный размер [ править ]
Размерность многообразия зависит от базового поля, относительно которого определено евклидово пространство. Хотя анализ обычно предполагает, что многообразие находится над действительными числами , иногда при изучении комплексных многообразий и алгебраических многообразий полезно работать с комплексными числами . Комплексное число ( x + iy ) имеет действительную часть x и мнимую часть y , где x и y - действительные числа; следовательно, комплексное измерение составляет половину реального измерения.
И наоборот, в алгебраически неограниченных контекстах единственная комплексная система координат может применяться к объекту, имеющему два реальных измерения. Например, обычная двумерная сферическая поверхность при задании комплексной метрики становится сферой Римана одного комплексного измерения. [3]
Разновидности [ править ]
Размерность алгебраического многообразия может быть определена различными эквивалентными способами. Наиболее интуитивно понятный способ - это, вероятно, измерение касательного пространства в любой регулярной точке алгебраического многообразия . Другой интуитивно понятный способ - определить размерность как количество гиперплоскостей , необходимых для пересечения с разнообразием, которое сокращается до конечного числа точек (размерность ноль). Это определение основано на том факте, что пересечение многообразия с гиперплоскостью уменьшает размерность на единицу, если только гиперплоскость не содержит многообразия.
Алгебраическое множество является конечным объединением алгебраических многообразий, его размерность максимум размеров его компонентов. Он равен максимальной длине цепочек подмногообразий данного алгебраического множества (длина такой цепочки равна числу " ").
Каждое разнообразие можно рассматривать как алгебраический стек , и его размерность как разновидность согласуется с его размерностью как стек. Однако есть много стопок, которые не соответствуют разновидностям, и некоторые из них имеют отрицательный размер. В частности, если V - многообразие размерности m, а G - алгебраическая группа размерности n, действующая на V , то фактор-стек [ V / G ] имеет размерность m - n . [4]
Измерение Крулла [ править ]
Размерность Крулля из коммутативного кольца является максимальной длиной цепей простых идеалов в ней, цепи длины п является последовательностью простых идеалов , связанных с включением. Оно сильно связано с размерностью алгебраического многообразия из-за естественного соответствия между подмногообразиями и простыми идеалами кольца многочленов на многообразии.
Для алгебры над полем размерность как векторного пространства конечна тогда и только тогда, когда ее размерность Крулля равна 0.
Топологические пространства [ править ]
Для любого нормального топологического пространства X , то Размерность Лебега на X определяется как наименьшее целое число п , для которых имеет место следующее: любой открытое покрытие имеет открытое покрытие (второе открытое покрытие , где каждый элемент является подмножеством элемент в первая крышка), так что ни одна точка не входит более чем в n + 1 элемент. В этом случае dim X = n . Для многообразия X это совпадает с указанной выше размерностью. Если такого целого n не существует, то размерность X называется бесконечной, и пишут dimX = ∞ . Более того, X имеет размерность −1, т.е. dim X = −1 тогда и только тогда, когда X пусто. Это определение покрывающей размерности можно расширить с класса нормальных пространств на все тихоновские пространства, просто заменив термин «открытый» в определении термином « функционально открытый ».
Индуктивная размерность может быть определена индуктивно следующим образом . Считайте дискретный набор точек (например, конечный набор точек) 0-мерным. Перетаскивая 0-мерный объект в каком-либо направлении, можно получить одномерный объект. Перетаскивая одномерный объект в новом направлении , можно получить двухмерный объект. В общем случае получают ( n + 1 ) -мерный объект, перетаскивая n- мерный объект в новом направлении. Индуктивная размерность топологического пространства может относиться к малой индуктивной размерности или большой индуктивной размерности., и основан на аналогии, что в случае метрических пространств ( n + 1 ) -мерные шары имеют n -мерные границы , что позволяет индуктивное определение, основанное на размерности границ открытых множеств. Более того, граница дискретного набора точек - это пустое множество, и поэтому можно считать, что пустое множество имеет размерность -1. [5]
Аналогично, для класса комплексов CW размерность объекта равна наибольшему n, для которого n -скелет нетривиален. Интуитивно это можно описать следующим образом: если исходное пространство можно непрерывно деформировать в совокупность треугольников более высоких измерений, соединенных своими гранями со сложной поверхностью, то размерность объекта - это размерность этих треугольников. [ необходима цитата ]
Измерение Хаусдорфа [ править ]
Хаусдорфову полезен для изучения структурно сложных наборов, особенно фракталов . Размерность Хаусдорфа определена для всех метрических пространств и, в отличие от измерений, рассмотренных выше, также может иметь нецелые действительные значения. [6] Размер ящика или измерение Минковского - вариант той же идеи. В общем, существует больше определений фрактальных размерностей, которые работают для очень нерегулярных множеств и достигают нецелочисленных положительных вещественных значений. Было обнаружено, что фракталы полезны для описания многих природных объектов и явлений. [7] [ необходима страница ] [8] [ необходима страница]
Гильбертовы пространства [ править ]
Каждое гильбертово пространство допускает ортонормированный базис , и любые два таких базиса для конкретного пространства имеют одинаковую мощность . Эта мощность называется размерностью гильбертова пространства. Это измерение конечно тогда и только тогда, когда измерение Гамеля пространства конечно, и в этом случае два измерения совпадают.
В физике [ править ]
Пространственные размеры [ править ]
Теории классической физики описывают три физических измерения : из определенной точки в пространстве , основные направления, в которых мы можем двигаться, - это вверх / вниз, влево / вправо и вперед / назад. Движение в любом другом направлении можно выразить в терминах этих трех. Движение вниз - то же самое, что движение вверх на отрицательное расстояние. Движение по диагонали вверх и вперед - это то же самое, что и название направления; т.е. движение в линейной комбинации вверх и вперед. В простейшей форме: линия описывает одно измерение, плоскость описывает два измерения, а куб описывает три измерения. (См. Пространство и декартова система координат .)
Количество измерений | Примеры систем координат | |||
|---|---|---|---|---|
| 1 |
| |||
| 2 |
| |||
| 3 |
|
Время [ править ]
Временное измерение , или измерение времени , это измерение времени. По этой причине время часто называют « четвертым измерением », но это не означает, что это пространственное измерение. Временное измерение - это один из способов измерения физических изменений. Это воспринимается иначе, чем три пространственных измерения, поскольку существует только одно из них, и что мы не можем свободно перемещаться во времени, а субъективно двигаться в одном направлении .
Уравнения, используемые в физике для моделирования реальности, не трактуют время так, как его обычно воспринимают люди. Уравнения классической механики являются симметричными относительно времени , и уравнения квантовой механики , как правило , симметрична , если и время и другие величины (например, заряда и четности ) поменялись местами. В этих моделях восприятие времени, текущего в одном направлении, является артефактом законов термодинамики (мы воспринимаем время как текущее в направлении увеличения энтропии ).
Наиболее известная трактовка времени как измерения - это специальная теория относительности Пуанкаре и Эйнштейна (и расширенная до общей теории относительности ), которая рассматривает воспринимаемое пространство и время как компоненты четырехмерного многообразия , известного как пространство-время , а в специальном плоский корпус как пространство Минковского .
Дополнительные параметры [ править ]
В физике общепринятой нормой являются три измерения пространства и одно временное. Однако есть теории, которые пытаются объединить четыре фундаментальные силы , вводя дополнительные измерения / гиперпространство . В частности, теория суперструн требует 10 измерений пространства-времени и происходит от более фундаментальной 11-мерной теории, условно называемой М-теорией, которая включает пять ранее различных теорий суперструн. Теория супергравитациитакже продвигает 11D пространство-время = 7D гиперпространство + 4 общих измерения. На сегодняшний день нет прямых экспериментальных или наблюдательных данных, подтверждающих существование этих дополнительных измерений. Если гиперпространство существует, оно должно быть скрыто от нас каким-то физическим механизмом. Одна хорошо изученная возможность состоит в том, что дополнительные измерения могут быть «свернуты» в таких крошечных масштабах, что будут фактически невидимы для текущих экспериментов. Ограничения на размер и другие свойства дополнительных измерений устанавливаются экспериментами с частицами [ требуется пояснение ], например, на Большом адронном коллайдере . [9]
В 1921 году теория Калуцы-Клейна представила 5D, включая дополнительное измерение пространства. На уровне квантовой теории поля теория Калуцы – Клейна объединяет гравитацию с калибровочными взаимодействиями, основанную на понимании того, что гравитация, распространяющаяся в малых, компактных дополнительных измерениях, эквивалентна калибровочным взаимодействиям на больших расстояниях. В частности, когда геометрия дополнительных измерений тривиальна, она воспроизводит электромагнетизм . Однако при достаточно высоких энергиях или коротких расстояниях эта установка все еще страдает от тех же патологий, которые, как известно, препятствуют прямым попыткам описать квантовую гравитацию . Следовательно, эти модели по-прежнему требуют УФ-доработки.того типа, который предназначена предоставить теория струн. В частности, теория суперструн требует шести компактных измерений (6D-гиперпространство), образующих многообразие Калаби – Яу . Таким образом, теорию Калуцы-Клейна можно рассматривать либо как неполное описание само по себе, либо как подмножество построения модели теории струн.
В дополнение к небольшим и свернутым дополнительным измерениям могут быть дополнительные измерения, которые вместо этого не очевидны, потому что материя, связанная с нашей видимой Вселенной, локализована в (3 + 1) -мерном подпространстве. Таким образом, дополнительные размеры не обязательно должны быть маленькими и компактными, но могут быть большими дополнительными размерами . D-браны - это динамические протяженные объекты различной размерности, предсказанные теорией струн, которые могут играть эту роль. Они обладают тем свойством, что возбуждения открытой струны, связанные с калибровочными взаимодействиями, ограничены браной.их конечными точками, в то время как замкнутые струны, которые опосредуют гравитационное взаимодействие, могут свободно распространяться во все пространство-время или «балку». Это может быть связано с тем, почему гравитация экспоненциально слабее, чем другие силы, поскольку она эффективно растворяется, когда распространяется в объем более высокого измерения.
Некоторые аспекты физики браны были применены к космологии . Например, космология бранного газа [10] [11]пытается объяснить, почему существует три измерения пространства, используя топологические и термодинамические соображения. Согласно этой идее, это было бы потому, что три - это наибольшее количество пространственных измерений, где струны могут пересекаться. Если изначально существует много витков струн вокруг компактных размеров, пространство может расшириться до макроскопических размеров только после того, как эти обмотки будут устранены, что требует, чтобы струны противоположно намотаны, чтобы найти друг друга и аннигилировать. Но струны могут найти друг друга только для того, чтобы аннигилировать со значимой скоростью в трех измерениях, поэтому следует, что только три измерения пространства могут увеличиваться в размерах при такой начальной конфигурации.
Дополнительные измерения называются универсальными, если все поля могут одинаково свободно распространяться внутри них.
В компьютерной графике и пространственных данных [ править ]
Несколько типов цифровых систем основаны на хранении, анализе и визуализации геометрических фигур, включая программное обеспечение для иллюстраций , системы автоматизированного проектирования и географические информационные системы . Различные векторные системы используют самые разные структуры данных для представления фигур, но почти все они в основном основаны на наборе геометрических примитивов, соответствующих пространственным измерениям: [12]
- Точка (0-мерная), единственная координата в декартовой системе координат .
- Линия или полилиния (1-мерная), обычно представленная в виде упорядоченного списка точек, взятых из непрерывной линии, после чего ожидается, что программное обеспечение интерполирует промежуточную форму линии в виде прямых или изогнутых сегментов линии.
- Многоугольник (2-мерный), обычно представляемый в виде линии, которая замыкается в своих конечных точках, представляя границу двухмерной области. Ожидается, что программное обеспечение будет использовать эту границу для разделения двухмерного пространства на внутреннее и внешнее.
- Поверхность (трехмерная), представленная с использованием различных стратегий, например, многогранник, состоящий из соединенных граней многоугольника. Ожидается, что программное обеспечение будет использовать эту поверхность для разделения трехмерного пространства на внутреннее и внешнее.
Часто в этих системах, особенно в ГИС и картографии , представление реальных явлений может иметь другое (обычно более низкое) измерение, чем представляемое явление. Например, город (двухмерный регион) может быть представлен как точка, или дорога (трехмерный объем материала) может быть представлена как линия. Это размерное обобщениекоррелирует с тенденциями в пространственном познании. Например, вопрос о расстоянии между двумя городами предполагает концептуальную модель городов в виде точек, а указание направлений, включающих движение «вверх», «вниз» или «вдоль» дороги, подразумевает одномерную концептуальную модель. Это часто делается в целях эффективности данных, визуальной простоты или когнитивной эффективности и приемлемо, если различие между представлением и представленным понятно, но может вызвать путаницу, если пользователи информации предполагают, что цифровая форма является идеальным представлением реальности. (т.е. веря, что дороги на самом деле являются линиями).
Сети и измерение [ править ]
Некоторые сложные сети характеризуются фрактальной размерностью . [13] Концепция измерения может быть обобщена на сети, встроенные в пространство. [14] Размерность характеризует их пространственные ограничения.
В литературе [ править ]
В научно-фантастических текстах часто упоминается понятие «измерение», когда речь идет о параллельных или альтернативных вселенных или других воображаемых планах существования . Это использование происходит из идеи, что для путешествия в параллельные / альтернативные вселенные / планы существования нужно путешествовать в направлении / измерении помимо стандартных. Фактически, другие вселенные / планы находятся на небольшом расстоянии от нашей, но это расстояние находится в четвертом (или более высоком) пространственном (или непространственном) измерении, а не в стандартных.
Одна из самых известных научно-фантастических историй об истинной геометрической размерности, которую часто рекомендуют в качестве отправной точки для тех, кто только начинает исследовать такие вопросы, - это повесть Эдвина А. Эбботта « Флатландия» 1884 года . Исаак Азимов в своем предисловии к изданию Signet Classics 1984 года охарактеризовал Флатландию как «лучшее введение в способ восприятия измерений».
Идея других размеров была включена во многие ранние рассказы научной фантастики, появляясь на видном месте , например, в Miles J. Breuer «s аппендикс и зрелищ (1928) и Мюррей Лейнстер » s Пятое измерение катапульта (1931); и нерегулярно появлялся в научной фантастике к 1940-м годам. К классическим историям, затрагивающим другие измерения, относятся: « И он построил кривый дом» Роберта А. Хайнлайна (1941), в котором калифорнийский архитектор проектирует дом на основе трехмерной проекции тессеракта; и « Тигр у хвоста» и «Вселенная между ними» Алана Э. Нурса (оба 1951). Еще одна ссылкаРоман Мадлен Л'Энгл « Морщинка во времени» (1962), в котором пятое измерение используется как способ «тессерации Вселенной» или «складывания» пространства для быстрого перемещения по нему. Четвертое и пятое измерения также являются ключевыми компонентами книги Уильяма Слейтора «Мальчик, который полностью изменил себя » .
В философии [ править ]
Иммануил Кант в 1783 году писал: «Что везде пространство (которое само не является границей другого пространства) имеет три измерения и что пространство в целом не может иметь больше измерений, основано на предположении, что не более трех линий могут пересекаться справа. Это предложение вообще не может быть показано из понятий, оно непосредственно опирается на интуицию и даже на чистую интуицию a priori, потому что оно аподиктически (очевидно) достоверно ". [15]
«Пространство имеет четыре измерения» - это рассказ, опубликованный в 1846 году немецким философом и экспериментальным психологом Густавом Фехнером под псевдонимом «доктор Мизес». Главный герой сказки - тень, которая знает о других тенях и способна общаться с ними, но застряла на двухмерной поверхности. Согласно Фехнеру, этот «человек-тень» воспринимает третье измерение как измерение времени. [16] Эта история очень похожа на « Аллегорию пещеры », представленную в произведении Платона « Республика» ( ок. 380 г. до н. Э.).
Саймон Ньюкомб написал статью для Бюллетеня Американского математического общества в 1898 году под названием «Философия гиперпространства». [17] Линда Дэлримпл Хендерсон ввела термин «философия гиперпространства», используемый для описания письма, использующего высшие измерения для исследования метафизических тем, в своей диссертации 1983 года о четвертом измерении в искусстве начала двадцатого века. [18] Примеры «философов гиперпространства» включают Чарльза Ховарда Хинтона , первого писателя в 1888 году, использовавшего слово «тессеракт»; [19] и русский эзотерик П. Д. Успенский .
Дополнительные параметры [ править ]
| Геометрия |
|---|
|
| Геометры |
- Степени свободы
- в механике
- по физике и химии
- в статистике
- Внешний размер
- Показатель Херста
- Изопериметрический размер
- Метрический параметр
- Размер заказа
- q -размерность
- Фрактал ( q = 1)
- Корреляция ( q = 2)
См. Также [ править ]
- Измерение (хранилище данных)
- Таблицы размеров
- Размерный анализ
- Гиперпространство (значения)
- Внутренний размер
- Многомерный анализ
- Кривая заполнения пространства
- Среднее измерение
Темы по параметрам [ править ]
- Нуль
- Точка
- Нульмерное пространство
- Целое число
- Один
- Линия
- Изгиб
- Граф (комбинаторика)
- Настоящий номер
- Два
- Комплексное число
- Декартова система координат
- Список однородных мозаик
- Поверхность
- Три
- Платоново твердое тело
- Стереоскопия (трехмерное изображение)
- 3-х коллекторный
- Узлы
- Четыре
- Пространство-время
- Четвертое пространственное измерение
- Выпуклый правильный 4-многогранник
- Кватернион
- 4-х коллекторный
- Четвертое измерение в искусстве
- Четвертое измерение в литературе
- Высшие измерения
- по математике
- Октонион
- Векторное пространство
- Проклятие размерности
- в физике
- Теория Калуцы – Клейна
- Теория струн
- М-теория
- по математике
- Бесконечный
- Гильбертово пространство
- Функциональное пространство
Ссылки [ править ]
Эта статья требует дополнительных ссылок для проверки . ( май 2010 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения ) |
- ^ "Любопытно об астрономии" . Curious.astro.cornell.edu. Архивировано из оригинала на 2014-01-11 . Проверено 3 марта 2014 .
- ^ «MathWorld: Dimension» . Mathworld.wolfram.com. 2014-02-27. Архивировано 25 марта 2014 года . Проверено 3 марта 2014 .
- ^ Яу, Шинг-Тунг; Надис, Стив (2010). «4. Слишком хорошо, чтобы быть правдой» . Форма внутреннего пространства: теория струн и геометрия скрытых измерений Вселенной . Основные книги. С. 60–. ISBN 978-0-465-02266-3.
- ^ Fantechi, Барбара (2001), "Стеки для всех" (PDF) , Европейский конгресс математики Том I , Программируемое. Math., 201 , Birkhäuser, pp. 349–359, архивировано (PDF) из оригинала 17 января 2006 г.
- ^ Hurewicz, Витольд; Уоллман, Генри (2015). Теория измерений (ПМС-4), Том 4 . Издательство Принстонского университета . п. 24. ISBN 978-1-4008-7566-5. Выдержка страницы 24
- ^ Фрактальная размерность архивация 2006-10-27 в Wayback Machine , Бостонский университет Факультет математики и статистике
- ^ Бунде, Армин; Хавлин, Шломо , ред. (2012) [1991]. Фракталы и неупорядоченные системы (2-е изд.). Springer. ISBN 978-3-642-84868-1.
- ^ Бунде, Армин; Хавлин, Шломо , ред. (2013) [1994]. «1. Краткое введение в фрактальную геометрию 1.2.1 Кривая Коха» . Фракталы в науке . Springer. С. 3–. ISBN 978-3-642-77953-4.
- ^ CMS Collaboration (2011). «Поиск микроскопических сигнатур черных дыр на Большом адронном коллайдере». Phys. Lett. B . 697 (5): 434–453. arXiv : 1012,3375 . Bibcode : 2011PhLB..697..434C . DOI : 10.1016 / j.physletb.2011.02.032 . S2CID 118488193 . CMS-EXO-10-017, CERN-PH-EP-2010-073.
- ^ Brandenberger, R .; Вафа, К. (1989). «Суперструны в ранней вселенной». Ядерная физика Б . 316 (2): 391–410. Bibcode : 1989NuPhB.316..391B . DOI : 10.1016 / 0550-3213 (89) 90037-0 .
- ↑ Скотт Уотсон, Космология газа Бран, Архивировано 27октября2014 г. в Wayback Machine (pdf).
- ^ Векторные модели данных , Основы географических информационных систем , Saylor Academy, 2012
- ^ Песня, Хаоминг; Хавлин, Шломо ; Максе, Эрнан А. (2005). «Самоподобие сложных сетей». Природа . 433 (7024): 392–395. arXiv : cond-mat / 0503078v1 . Bibcode : 2005Natur.433..392S . DOI : 10,1038 / природа03248 . PMID 15674285 . S2CID 1985935 .
- ^ Дацин, Ли; Космидис, Космас; Бунде, Армин; Хавлин, Шломо (2011). «Измерение пространственно встроенных сетей» (PDF) . Физика природы . 7 (6): 481. Bibcode : 2011NatPh ... 7..481D . DOI : 10.1038 / nphys1932 .
- ^ Пролегомены , § 12
- ^ Banchoff, Томас Ф. (1990). «От плоской земли к гиперграфике: взаимодействие с более высокими измерениями» . Междисциплинарные научные обзоры . 15 (4): 364. DOI : 10,1179 / 030801890789797239 . Архивировано 14 апреля 2013 года.
- ^ Ньюкомб, Саймон (1898). «Философия гиперпространства» . Бюллетень Американского математического общества . 4 (5): 187. DOI : 10.1090 / S0002-9904-1898-00478-0 .
- ^ Крюгер, Runette (2007). «Искусство в четвертом измерении: придание формы форме - абстрактные картины Пита Мондриана» (PDF) . Пространства утопии: электронный журнал (5): 11. Архивировано (PDF) из оригинала 29.09.2011.
- ^ Пиковер, Clifford A. (2009), "Tesseract" , Математика Книга: От Пифагора до 57 - го измерения, 250 Вехи в истории математики , Sterling Publishing, стр. 282, ISBN 978-1-4027-5796-9, заархивировано из оригинала 30.03.2017.
Дальнейшее чтение [ править ]
- Мурти, Катта Г. (2014). «1. Системы одновременных линейных уравнений» (PDF) . Вычислительная и алгоритмическая линейная алгебра и n-мерная геометрия . Мировое научное издательство. DOI : 10,1142 / 8261 . ISBN 978-981-4366-62-5.
- Эбботт, Эдвин А. (1884). Флатландия: Многогранный роман . Лондон: Seely & Co.
- -. Флатландия: ... Проект Гутенберг .
- -; Стюарт, Ян (2008). Аннотированная равнина: многогранный роман . Основные книги. ISBN 978-0-7867-2183-2.
- Банчофф, Томас Ф. (1996). За пределами третьего измерения: геометрия, компьютерная графика и более высокие измерения . Научная американская библиотека. ISBN 978-0-7167-6015-3.
- Пиковер, Клиффорд А. (2001). Серфинг в гиперпространстве: понимание высших вселенных за шесть простых уроков . Издательство Оксфордского университета . ISBN 978-0-19-992381-6.
- Ракер, Руди (2014) [1984]. Четвертое измерение: к геометрии высшей реальности . Курьерская корпорация. ISBN 978-0-486-77978-2. Предварительный просмотр Google
- Каку, Мичио (1994). Гиперпространство, научная одиссея через 10-е измерение . Издательство Оксфордского университета. ISBN 978-0-19-286189-4.
- Краусс, Лоуренс М. (2005). Прячась в зеркале . Викинг Пресс. ISBN 978-0-670-03395-9.
Внешние ссылки [ править ]
| В Wikiquote есть цитаты, связанные с: Dimension |
| Викискладе есть медиафайлы по теме Размеры . |
| В Wikisource есть текст статьи « Измерение» из Британской энциклопедии 1911 года . |
- Коупленд, Эд (2009). «Дополнительные измерения» . Шестьдесят символов . Brady Харан для Ноттингемского университета .


