Комбинаторные виды

Эта статья включает в себя список общих ссылок , но он остается в значительной степени непроверенным, поскольку в нем отсутствует достаточное количество соответствующих встроенных ссылок . Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Июнь 2018 г. ) ( Узнайте, как и когда удалить этот шаблон сообщения )

В комбинаторной математике теория комбинаторных видов представляет собой абстрактный систематический метод анализа дискретных структур с точки зрения производящих функций . Примерами дискретных структур являются ( конечные ) графы , перестановки , деревья, и так далее; с каждым из них связана производящая функция, которая подсчитывает, сколько структур определенного размера. Одна из целей теории видов - иметь возможность анализировать сложные структуры, описывая их в терминах преобразований и комбинаций более простых структур. Эти операции соответствуют эквивалентным манипуляциям с производящими функциями, поэтому создание таких функций для сложных структур намного проще, чем с помощью других методов. Теория была представлена, тщательно разработана и применена канадской группой людей вокруг Андре Хояла .

Сила теории проистекает из ее уровня абстракции. «Описание формат» структуры (например, смежность списка по сравнению с матрицей смежности для графов) не имеет никакого значения, потому что вид чисто алгебраические. Теория категорий предоставляет полезный язык для концепций, которые здесь возникают, но не обязательно понимать категории, прежде чем иметь возможность работать с видами.

Категория видов эквивалентна категории симметричных последовательностей в конечных множествах. ^[1]

Определение вида [ править ]

Схематическая иллюстрация комбинаторной структуры видов на пяти элементах с использованием диаграммы Лабелля

Любая структура - экземпляр определенного вида - связана с некоторым набором , и часто существует много возможных структур для одного и того же набора. Например, можно построить несколько разных графов, метки узлов которых взяты из одного и того же заданного набора. При этом для возведения конструкций можно было использовать любой набор. Разница между одним видом и другим состоит в том, что они строят разные наборы структур из одного и того же основного набора.

Это приводит к формальному определению комбинаторного вида . Пусть будет категория из конечных множеств , с морфизмами из категории , являющейся биекции между этими множествами. Вида является функтор ^[2]${\ displaystyle {\ mathcal {B}}}$

${\ displaystyle F \ двоеточие {\ mathcal {B}} \ to {\ mathcal {B}}.}$

Для каждого конечного множества А в , конечное множество Р [ ] ^{[примечание 1]} называется множество F -структуры на А , или множество структур вида F на A . Далее, по определению функтора, если φ является биекцией между множествами A и B , то F [φ] является биекцией между множествами F -структур F [ A ] и F [ B ], называемой переносом F- конструкции вдоль φ . ^[3]${\ displaystyle {\ mathcal {B}}}$

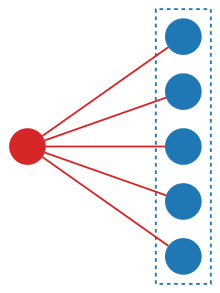
Например, «вид перестановок» ^[4] отображает каждое конечное множество A в множество всех перестановок A , и каждая биекция из A в другое множество B естественным образом индуцирует биекцию из множества всех перестановок A в множество все перестановки B . Точно так же «виды разделов» могут быть определены путем присвоения каждому конечному набору набора всех его разделов , а «виды набора мощности» назначают каждому конечному набору его набор мощности . На соседней диаграмме показана конструкция из пяти элементов: дуги соединяют структуру (красный цвет) с элементами (синий цвет), из которых он построен.

Поскольку существует взаимно однозначное соответствие между двумя конечными множествами тогда и только тогда , когда оба множества имеют одинаковую мощность (количество элементов) для каждого конечного множества А , мощность , которая конечна, зависит только от мощности A . (Это следует из формального определения функтора. ^{[Примечание 2]} ) В частности, можно определить экспоненциальный производящий ряд F ( x ) вида F : ^[5]${\ displaystyle F [A]}$

${\ displaystyle F (x) = \ sum _ {n \ geq 0} \ operatorname {Card} F [n] {\ frac {x ^ {n}} {n!}}}$

где - мощность для любого множества A, имеющего n элементов; например, .${\ displaystyle \ operatorname {Card} F [n]}$${\ displaystyle F [A]}$${\ Displaystyle А = \ {1,2, \ точки, п \}}$

Некоторые примеры: письмо ,${\ displaystyle f_ {n} = \ operatorname {Card} F [n]}$

• Вид множеств (традиционно называемый E от французского « ансамбль », что означает «множество») - это функтор, который отображает A в { A }. Тогда так .${\ displaystyle f_ {n} = 1}$${\displaystyle E(x)=e^{x}}$
• Вид S из перестановок , описанных выше, есть . .${\displaystyle f_{n}=n!}$${\displaystyle S(x)=1/(1-x)}$
• Вид T ₂ пар (2- кортежей ) - это функтор, переводящий множество A в A ² . Потом и .${\displaystyle f_{n}=n^{2}}$${\displaystyle T_{2}(x)=x(x+1)e^{x}}$

Исчисление видов [ править ]

Арифметика над производящими функциями соответствует некоторым «естественным» операциям над видами. Основные операции - это сложение, умножение, композиция и дифференцирование; также необходимо определить равенство по видам. В теории категорий уже есть способ описать, когда два функтора эквивалентны: естественный изоморфизм . В этом контексте это просто означает, что для каждого A существует биекция между F -структурами на A и G -структурами на A , которая «хорошо себя ведет» во взаимодействии с транспортом. Виды с одинаковой производящей функцией могут не быть изоморфными, но изоморфные виды всегда имеют одну и ту же производящую функцию.

Дополнение [ править ]

Сложение видов определяется непересекающимся объединением множеств и соответствует выбору между структурами. ^[6] Для видов F и G определите ( F + G ) [ A ] как дизъюнктное объединение (также обозначаемое «+») F [ A ] и G [ A ]. Отсюда следует, что ( F  +  G ) ( x ) =  F ( x ) +  G ( x ). В качестве демонстрации возьмем E ⁺быть разновидностями непустых множеств, производящая функция которых E ⁺ ( x ) =  e ^x  - 1, а 1 - разновидностями пустого множества , производящая функция которых равна 1 ( x ) = 1. Отсюда следует, что E  =  1  +  E ⁺ : словами, «набор либо пуст, либо не пуст». Подобные уравнения можно рассматривать как относящиеся к отдельной структуре, а также ко всему набору структур.

Первоначальное определение вида вдохновило исследователей на три направления. ^{[ необходима цитата ]}

- С категориальной стороны, требуется более крупный фрейм для содержания и продукта, и сопродукта . Цена - это потеря индекса цикла.

- Другой подход - это кольца или оснастки Burnside . Суммирование представлений Бернсайда - это формальная нотация, используемая при разработке теории таблиц оценок.

- Наконец, обычное определение не принимает во внимание функториальность и тот факт, что вид, даже если рассматривать его как правило, уникален. Для правила F не существует второго правила F для получения непересекающейся суммы F + F. В этом подходе определение суммирования фактически является определением на примере. Преимущество - естественная вставка указателя цикла в качестве электроинструмента.

Умножение [ править ]

Размножение видов несколько сложнее. Можно просто взять декартово произведение множеств в качестве определения, но комбинаторная интерпретация этого не совсем верна. (См. Ниже об использовании этого вида продукта.) Вместо того, чтобы складывать две несвязанные структуры в один и тот же набор, оператор умножения использует идею разделения набора на два компонента, конструируя F -структуру на одном и G - структура с другой. ^[7]

${\displaystyle (F\cdot G)[A]=\sum _{A=B+C}F[B]\times G[C].}$

Это объединение непересекающихся по всем возможным двоичным разделов  A . Несложно показать, что умножение ассоциативно и коммутативно (с точностью до изоморфизма ) и дистрибутивно по сложению. Что касается производящего ряда, ( F  ·  G ) ( x ) =  F ( x ) G ( x ).

На диаграмме ниже показана одна возможная ( F  ·  G ) -структура на множестве из пяти элементов. F -структуры (красная) поднимают три элемента базового набора, а G -структуры (светло - голубой) принимают все остальное. Другие структуры будут иметь F и G, разделяющие множество по-другому. Множество ( F  ·  G ) [ A ], где A - базовое множество, представляет собой несвязное объединение всех таких структур.

Сложение и умножение видов - наиболее полное выражение правил подсчета суммы и произведения.

Состав [ править ]

Состав , также называемый замещением, снова более сложен. Основная идея заключается в замене компонентов F на G -структуры, образующие ( F ∘ G ). ^[8] Как и в случае умножения, это делается путем разделения входного множества A ; непересекающиеся подмножества даны G для создания G -структур, а множество подмножеств дано F , чтобы образовать F -структуру, соединяющую G -структуры. Для работы G требуется сопоставить пустой набор с самим собой. Формальное определение:

${\displaystyle (F\circ G)[A]=\sum _{\pi \in P[A]}(F[\pi ]\times \prod _{B\in \pi }G[B]).}$

Здесь Р является видом перегородок, поэтому P [ ] есть множество всех разбиений A . Это определение говорит, что элемент ( F  ∘  G ) [ A ] состоит из F -структуры на некотором разбиении A и G-структуры на каждой компоненте разбиения. Производящий ряд равен .${\displaystyle (F\circ G)(x)=F(G(x))}$

Одна такая структура показана ниже. Три G-структуры (голубые) разделяют пятиэлементный базовый набор между собой; затем строится F-структура (красная) для соединения G-структур .

Эти две последние операции можно проиллюстрировать на примере деревьев. Во-первых, определите X как разновидность "одиночка", производящий ряд которой равен X ( x ) =  x . Тогда вид корневых деревьев Ar (от французского « древовидность ») определяется рекурсивно как Ar  =  X  ·  E ( Ar ). Это уравнение говорит, что дерево состоит из одного корня и набора (под) деревьев. Рекурсия не требует явного базового случая: она генерирует деревья только в контексте применения к некоторому конечному набору. Один из способов подумать об этом заключается в том, что Arфунктор применяется многократно к «предложениям» элементы из множества - каждый раз , когда один элемент принимается X , а остальные распределены по E среди Ar поддерев, пока нет больше элементов , чтобы дать к E . Это показывает, что алгебраические описания видов сильно отличаются от спецификаций типов в таких языках программирования, как Haskell .

Аналогично, разновидность P может быть охарактеризована как P  =  E ( E ⁺ ): «раздел - это попарно непересекающееся множество непустых множеств (использующее все элементы входного множества)». Экспоненциальный производящий ряд для P равен , который является рядом чисел Белла .${\displaystyle P(x)=e^{(e^{x}-1)}}$

Дифференциация [ править ]

Дифференциация видов интуитивно соответствует построению «построек с дырой», как показано на иллюстрации ниже.

Формально ^[9]

${\displaystyle (F')[A]=F[A\uplus \{\star \}],}$

где какой-то выдающийся новый элемент, отсутствующий в .${\displaystyle \star }$${\displaystyle A}$

Чтобы дифференцировать связанный экспоненциальный ряд, последовательность коэффициентов должна быть сдвинута на одну позицию влево (потеря первого члена). Это предлагает определение вида: F ' [ A ] =  F [ A  + {*}], где {*} - одноэлементный набор, а «+» - дизъюнктное объединение. Более продвинутые части теории видов широко используют дифференциацию для построения и решения дифференциальных уравнений для видов и рядов. Идея добавления (или удаления) отдельной части структуры является мощной: ее можно использовать для установления отношений между, казалось бы, несвязанными видами.

Например, рассмотрим структуру вида L линейных порядков - списки элементов основного набора. Удаление элемента из списка разбивает его на две части (возможно, пустые); в символах, это L»  =  L · L . Экспоненциальная производящая функция L равна L ( x ) = 1 / (1 -  x ), и действительно:

${\displaystyle {\frac {d}{dx}}{(1-x)}^{-1}={(1-x)}^{-2}.}$

Вид С циклических перестановок принимает множество А на множество всех циклов на A . Удаление одного элемента из цикла уменьшает его в список: С»  =  л . Мы можем интегрировать производящую функцию L , чтобы произвести , что для  C .

${\displaystyle C(x)=\int _{0}^{x}{\frac {dt}{1-t}}=\log {\frac {1}{1-x}}.}$

Хорошим примером интеграции видов является завершение линии (координированной полем) с бесконечной точкой и получение проективной линии.

Дальнейшие операции [ править ]

Есть множество других манипуляций, которые можно проводить с видами. Они необходимы для выражения более сложных структур, таких как ориентированные графы или биграфы .

При наведении выделяется один элемент конструкции. ^[10] Для вида F соответствующий точечный вид F ^• определяется как F ^• [ A ] = A × F [ A ]. Таким образом, каждая F ^• -структура является F-структурой с одним выделенным элементом. Указание связано с дифференцированием соотношением F ^• = X · F ' , поэтому F ^• ( x ) = x F' ( x). Вид остроконечных множеств , E ^• , особенно важен как строительный блок для многих более сложных конструкций.

Декартово произведение двух видов ^{[ править ]} является одним из видов , которые могут создавать две структуры на том же наборе в то же самое время. Он отличается от обычного оператора умножения тем, что все элементы базового набора разделяются между двумя структурами. ( F × G ) -структура может рассматриваться как суперпозиция F-структуры и G-структуры . Биграфы можно описать как суперпозицию графа и набора деревьев: каждый узел биграфа является частью графа и в то же время частью некоторого дерева, которое описывает, как узлы вложены. Производящая функция ( F × G ) ( x) является произведением Адамара или коэффициентов F ( x ) и G ( x ).

Вид E ^• × E ^• можно рассматривать как делающий два независимых выбора из базового набора. Две точки могут совпадать, в отличие от X · X · E , где они вынуждены быть разными.

В качестве функторов виды F и G могут быть объединены функциональной композицией : ^{[ необходима цитата ]} (используется квадратный символ, потому что круг уже используется для подстановки). Это строит F -структуре на множестве всех G -структурами на множестве A . Например, если Р является функтор принимает набор для его набора мощности, структура из составленных видов является некоторое подмножество G -структуры на A . Если теперь взять G за E ^• × E ^•${\displaystyle (F\,\Box \,G)[A]=F[G[A]]}$сверху мы получаем виды ориентированных графов с разрешенными петлями. (Ориентированный граф - это набор ребер, а ребра - это пары узлов: таким образом, граф - это подмножество набора пар элементов набора узлов A. ) Другие семейства графов, а также многие другие структуры могут быть определенным таким образом.

Программное обеспечение [ править ]

Операции с видами поддерживаются SageMath ^[11] и, с помощью специального пакета, также Haskell . ^{[12] [13]}

Варианты [ править ]

• Вид из k сортов является функтором . Здесь производимые конструкции могут иметь элементы, взятые из разных источников. ^{[ необходима цитата ]}${\displaystyle {\mathcal {B}}^{k}\rightarrow {\mathcal {B}}}$
• Функтор к , категории R -weighted наборов для R в кольце степенных рядов, представляет собой взвешенные разновидности . ^{[ необходима цитата ]}${\displaystyle {\mathcal {B}}_{R}}$

Если заменить «конечные множества с биекциями» на «конечные векторные пространства с линейными преобразованиями», то получится понятие полиномиального функтора (после наложения некоторого условия конечности). ^{[ необходима цитата ]}

См. Также [ править ]

• Контейнер (теория типов)

Заметки [ править ]

Ссылки [ править ]

• Андре Жоял, Теория комбинаторики серии форм , Успехи в математике 42: 1–82 (1981).
• Лабель, Жак. Quelques espèces sur les ensembles de petite cardinalité. , Аня. Sc. Математика. Квебек, 9.1 (1985): 31-58.
• Дж. Лабелль и Ю. Н. Йе, Связь между кольцами Бернсайда и комбинаторными видами , Журнал комбинаторной теории, серия A 50, (1989) 269–284
• Yves Chiricota, Classification des espèces moléculaires de degré 6 et 7 , Ann. Sci. Математика. Квебек 17 (1993), нет. 1, 1 л – 37.
• François Bergeron, Gilbert Labelle, Pierre Leroux, Théorie des espèces et combinatoire des structure arborescentes , LaCIM, Montréal (1994). Английская версия: Комбинаторные виды и древовидные структуры , Cambridge University Press (1998).
• Кербер, Адальберт (1999), Прикладные действия конечных групп, алгоритмы и комбинаторика, 19 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-65941-9 , MR 1716962, OCLC 247593131 

Внешние ссылки [ править ]

• Вайсштейн, Эрик В. «Виды» . MathWorld .
• https://ncatlab.org/nlab/show/species