В математике поток сокращения кривой - это процесс, который изменяет гладкую кривую на евклидовой плоскости , перемещая ее точки перпендикулярно кривой со скоростью, пропорциональной кривизне . Поток с сокращением кривой является примером геометрического потока и одномерным случаем потока средней кривизны . Другие названия одного и тот же процесс включают евклидовую поток укорочения , геометрическое поток тепла , [1] и эволюцию длины дуги .
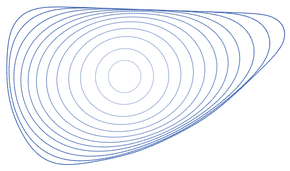
Поскольку точки любой гладкой простой замкнутой кривой перемещаются таким образом, кривая остается простой и гладкой. Он теряет площадь с постоянной скоростью, а его периметр уменьшается настолько быстро, насколько это возможно для любой непрерывной эволюции кривой. Если кривая невыпуклая, ее общая абсолютная кривизна монотонно уменьшается, пока не станет выпуклой. После выпуклости изопериметрическое соотношениекривой уменьшается по мере того, как кривая сходится к круглой форме, прежде чем схлопнуться к единственной точке сингулярности. Если две непересекающиеся простые гладкие замкнутые кривые эволюционируют, они остаются непересекающимися, пока одна из них не схлопнется в точку. Круг - единственная простая замкнутая кривая, которая сохраняет свою форму в потоке, сокращающем кривую, но некоторые кривые, которые пересекаются друг с другом или имеют бесконечную длину, сохраняют свою форму, в том числе мрачная кривая жнеца, бесконечная кривая, которая перемещается вверх, и спирали, которые вращаются. при этом оставаясь того же размера и формы.
Приближение к потоку сокращения кривой можно вычислить численно, аппроксимируя кривую как многоугольник и используя метод конечных разностей для расчета движения каждой вершины многоугольника. Альтернативные методы включают в себя вычисление свертки вершин многоугольника и затем повторную выборку вершин на результирующей кривой или многократное применение медианного фильтра к цифровому изображению , черные и белые пиксели которого представляют собой внутреннюю и внешнюю стороны кривой.
Течение с укорачиванием кривой первоначально изучалось как модель отжига металлических листов. Позже он был применен в анализе изображений, чтобы дать многомасштабное представление форм. Он также может моделировать системы реакции-диффузии и поведение клеточных автоматов . В чистой математике поток сокращения кривой можно использовать для поиска замкнутых геодезических на римановых многообразиях и в качестве модели поведения многомерных потоков.
Определения [ править ]
Поток представляет собой процесс , в котором точки математического пространства непрерывно изменяют свои места или свойство с течением времени. Более конкретно, в одномерном геометрическом потоке, таком как поток, укорачивающий кривую, точки, через которые проходит поток, принадлежат кривой , и что изменяется, так это форма кривой, ее вложение в евклидову плоскость, определяемую местоположением каждого из них. своих точек. [2] В потоке сокращения кривой каждая точка кривой перемещается в направлении вектора нормали к кривой со скоростью, пропорциональной кривизне . Для развивающейся кривой, представленной двухпараметрической функцией C ( s, t ), где s параметризует длину дуги вдоль кривой, а t параметрирует время в эволюции кривой, поток сокращения кривой может быть описан параболическим уравнением в частных производных
форма уравнения теплопроводности , где κ - кривизна, а n - единичный вектор нормали. [3]
Поскольку компоненты этого уравнения, длина дуги, кривизна и время, не зависят от перемещений и поворотов евклидовой плоскости, из этого следует, что поток, определяемый этим уравнением, инвариантен относительно перемещений и вращений (или, точнее, эквивариантен ). . Если масштабировать самолет с постоянным коэффициентом расширения, поток остается практически неизменным, но замедляется или ускоряется с тем же коэффициентом. [4]
Негладкие кривые [ править ]
Чтобы поток был хорошо определен, данная кривая должна быть достаточно гладкой, чтобы иметь непрерывную кривизну. Однако, как только поток начинается, кривая становится аналитической и остается таковой до тех пор, пока не достигнет сингулярности, в которой кривизна резко возрастет. Для гладкой кривой без пересечений единственная возможная сингулярность возникает, когда кривая схлопывается в точку, но погруженные кривые могут иметь особенности других типов. [5] В таких случаях с некоторой осторожностью можно продолжить обтекание этих сингулярностей до тех пор, пока вся кривая не сузится до единственной точки. [6]
Для простой замкнутой кривой с использованием расширения потока на негладкие кривые на основе метода установки уровня есть только две возможности. Кривые с нулевой мерой Лебега (включая все многоугольники и кусочно-гладкие кривые) мгновенно превращаются в гладкие кривые, после чего они развиваются, как любая гладкая кривая. Однако вместо этого кривые Осгуда с ненулевой мерой немедленно превращаются в топологическое кольцо с ненулевой площадью и гладкими границами. [7] В синусоидальной кривой тополога в пример , который мгновенно становится гладкой, несмотря на не даже будучи локально подключен; Примеры, подобные этому, показывают, что обратная эволюция потока, сокращающего кривую, может привести кривые с хорошим поведением к сложным сингулярностям за конечное время. [8]
Неевклидовы поверхности [ править ]
Поток сокращения кривой и многие результаты о потоке сокращения кривой можно обобщить с евклидовой плоскости на любое двумерное риманово многообразие . Во избежание дополнительных типов особенностей важно, чтобы многообразие было выпуклым на бесконечности ; это означает, что каждый компакт имеет компактную выпуклую оболочку , как определено с помощью геодезической выпуклости . Поток, сокращающий кривую, не может вызвать отклонение кривой от ее выпуклой оболочки, поэтому это условие не позволяет частям кривой достигать границы многообразия. [9]
Космические кривые [ править ]
Поток сокращения кривой также изучался для кривых в трехмерном евклидовом пространстве . Вектор нормали в этом случае может быть определен (как на плоскости) как производная касательного вектора по длине дуги, нормированная как единичный вектор; это один из компонентов системы Френе – Серре . Он плохо определен в точках нулевой кривизны, но произведение кривизны и вектора нормали остается четко определенным в этих точках, что позволяет определить поток сокращения кривой. Кривые в пространстве могут пересекать друг друга или сами себя в соответствии с этим потоком, и течение может приводить к сингулярностям на кривых; каждая особенность асимптотична плоскости. [10]Поток сокращения кривой для пространственных кривых использовался как способ определения обтекания сингулярностей на плоских кривых. [11]
За пределами кривых [ править ]
Можно расширить определение потока на более общие входные данные, чем кривые, например, используя выпрямляемые варифольды или метод установки уровня . Однако эти расширенные определения могут позволить частям кривых мгновенно исчезнуть или разрастаться до наборов ненулевой площади. [12]
Обычно изучаемый вариант проблемы включает сети непересекающихся внутри гладких кривых с соединениями, в которых пересекаются три или более кривых. Когда все стыки имеют ровно три кривые, пересекающиеся под углами 2 π / 3 (те же условия, которые наблюдаются в оптимальном дереве Штейнера или двумерной пене из мыльных пузырей ), течение краткосрочного периода четко определено. Однако в конечном итоге он может достичь сингулярного состояния с четырьмя или более кривыми, пересекающимися на стыке, и может быть более одного способа продолжить поток мимо такой сингулярности. [13]
Поведение [ править ]
Принцип уклонения, радиус и коэффициент растяжения [ править ]
Если две непересекающиеся гладкие простые замкнутые кривые одновременно подвергаются потоку, сокращающему кривую, они остаются не пересекающимися по мере развития потока. Причина в том, что, если две плавные кривые движутся таким образом, что создает пересечение, то во время первого пересечения кривые обязательно будут касаться друг друга, но не пересекаться. Но в такой ситуации кривизна двух кривых в точке касания неизбежно раздвигает их, а не сталкивает вместе в пересечение. По той же причине простая замкнутая кривая никогда не может пересечь сама себя. Это явление известно как принцип избегания. [14]
Принцип избегания подразумевает, что любая гладкая замкнутая кривая в конечном итоге должна достичь сингулярности, например точки бесконечной кривизны. Ведь, если заданная гладкая кривая C окружена кругом, обе они останутся не пересекающимися, пока существуют обе. Но окружающий круг сжимается под действием потока кривизны, оставаясь круглым, пока не схлопнется, и по принципу избегания C должен оставаться внутри него. Итак, если бы C никогда не достигал сингулярности, он был бы захвачен в единственной точке в то время, когда круг схлопывается, что невозможно для гладкой кривой. Это может быть определено количественно, наблюдая, что радиус наименьшего круга, который охватывает Cдолжен уменьшаться со скоростью, по крайней мере, такой же быстрой, как уменьшение радиуса круга, испытывающего такое же течение. [15]
Huisken (1998) количественно определяет принцип избегания для одной кривой в терминах отношения между длиной дуги (меньшей из двух дуг) и евклидовым расстоянием между парами точек, иногда называемым коэффициентом растяжения . Он показывает, что коэффициент растяжения строго уменьшается в каждом из его локальных максимумов, за исключением случая двух концов диаметра окружности, когда коэффициент растяжения постоянен на π . Это свойство монотонности подразумевает принцип избегания, поскольку, если кривая когда-либо коснется самой себя, коэффициент растяжения станет бесконечным в двух точках касания.
Длина [ править ]
По мере того как кривая претерпевает укорачивание кривой, ее длина L уменьшается со скоростью, определяемой формулой
где интервал берется по кривой, κ - кривизна, а s - длина дуги вдоль кривой. Подынтегральная функция всегда неотрицательна, и для любой гладкой замкнутой кривой существуют дуги, внутри которых она строго положительна, поэтому длина монотонно уменьшается. В более общем смысле, для любой эволюции кривых, нормальная скорость которых равна f , скорость изменения длины равна
что можно интерпретировать как отрицательный внутренний продукт между данной эволюцией и потоком, укорачивающим кривую. Таким образом, поток, сокращающий кривую, можно описать как градиентный поток по длине, поток, который (локально) уменьшает длину кривой как можно быстрее относительно L 2 нормы потока. Это свойство и дало название потоку, сокращающему кривую. [16]
Площадь [ править ]
Для простой замкнутой кривой площадь, ограниченная кривой, сжимается с постоянной скоростью 2 π единиц площади в единицу времени, независимо от кривой. Следовательно, общее время, за которое кривая сузится до точки, пропорционально ее площади, независимо от ее исходной формы. [17] Так как площадь кривой уменьшается с постоянной скоростью, и (согласно изопериметрическому неравенству ) круг имеет максимально возможную площадь среди простых замкнутых кривых заданной длины, из этого следует, что круги - самые медленные кривые, чтобы схлопнуться до точка под потоком, укорачивающим кривую. Все остальные кривые схлопываются меньше времени, чем круг такой же длины. [18]
Постоянная скорость уменьшения площади - единственный закон сохранения, которому удовлетворяет поток, сокращающий кривую. Это означает, что невозможно выразить «точку схода», в которой кривая в конечном итоге схлопывается, как интеграл по кривой от любой функции ее точек и их производных, потому что такое выражение привело бы к запрещенному второму закону сохранения. [19] Однако, комбинируя постоянную скорость потери площади с принципом избегания, можно доказать, что точка схода всегда находится внутри круга, концентричного с минимальным охватывающим кругом, площадь которого является разницей в площадях между охватывающими круг и заданная кривая. [20]
Полная абсолютная кривизна [ править ]
Общее абсолютное кривизна гладкой кривой является интегралом от абсолютного значения кривизны по длине дуги кривой,
Его также можно выразить как сумму углов между векторами нормалей в последовательных парах точек перегиба . Это 2 π для выпуклых кривых и больше для невыпуклых кривых, служащее мерой невыпуклости кривой. [21]
Новые точки перегиба не могут быть созданы потоком, сокращающим кривую. [22] Каждый из углов в представлении полной абсолютной кривизны в виде суммы монотонно уменьшается, за исключением моментов, когда две последовательные точки перегиба достигают того же угла или положения, что и друг друга, и обе исключаются. Следовательно, общая абсолютная кривизна никогда не может увеличиваться по мере развития кривой. Для выпуклых кривых он постоянен при 2 π, а для невыпуклых кривых монотонно убывает. [23]
Теорема Гейджа – Гамильтона – Грейсона [ править ]
Если гладкая простая замкнутая кривая подвергается потоку сокращения кривой, она остается гладко вложенной без самопересечений. Со временем он станет выпуклым , и после этого останется выпуклым. По истечении этого времени все точки кривой переместятся внутрь, и форма кривой будет сходиться к кругу, так как вся кривая сузится до одной точки. Такое поведение иногда резюмируют, говоря, что каждая простая замкнутая кривая сжимается до «круглой точки». [24]
Этот результат получен благодаря Майклу Гейджу , Ричарду С. Гамильтону и Мэтью Грейсону. Гейдж ( 1983 , 1984 ) доказал сходимость к окружности для выпуклых кривых, стягивающихся в точку. В частности, Гейдж показал, что изопериметрическое отношение (отношение квадрата длины кривой к площади, число, равное 4 π для круга и больше для любой другой выпуклой кривой) уменьшается монотонно и быстро. Гейдж и Гамильтон (1986) доказали, что все гладкие выпуклые кривые в конечном итоге стягиваются в точку без образования каких-либо других особенностей, а Грейсон (1987) доказал, что каждая невыпуклая кривая в конечном итоге станет выпуклой. [25] Эндрюс и Брайан (2011) предоставляют более простое доказательство результата Грейсона, основанное на монотонности фактора растяжения.
Подобные результаты могут быть распространены с замкнутых кривых на неограниченные кривые, удовлетворяющие локальному условию Липшица . Для таких кривых, если обе стороны кривой имеют бесконечную площадь, то развитая кривая остается гладкой и без сингулярностей все время. Однако, если одна сторона неограниченной кривой имеет конечную площадь, а кривая имеет конечную общую абсолютную кривизну, то ее эволюция достигает сингулярности во времени, пропорциональной площади на стороне конечной площади кривой, с неограниченной кривизной вблизи сингулярности. . [26] Для кривых, которые являются графиками достаточно хороших функций, асимптотических по лучу в каждом направлении, решение сходится по форме к уникальной форме, которая является асимптотической по отношению к тем же лучам. [27]Для сетей, образованных двумя непересекающимися лучами на одной прямой, вместе с двумя гладкими кривыми, соединяющими концы двух лучей, справедлив аналог теоремы Гейджа – Гамильтона – Грейсона, согласно которой область между двумя кривыми становится выпуклой, а затем сходится к форме vesica piscis . [28]
Особенности самопересечения кривых [ править ]
Кривые, которые имеют самопересечение, могут достигать сингулярностей, прежде чем сузиться до точки. Например, если лемниската (любая плавная погруженная кривая с одним пересечением, напоминающая цифру 8 или символ бесконечности ) имеет неравные площади в двух лепестках, то в конечном итоге меньшая доля схлопнется в точку. Однако, если два лепестка имеют равные площади, то они будут оставаться одинаковыми на протяжении всей эволюции кривой, а изопериметрическое отношение будет расходиться, когда кривая схлопнется до сингулярности. [4]
Когда локально выпуклая кривая самопересечения приближается к сингулярности, когда одна из ее петель сжимается, она либо сжимается самоподобным образом, либо асимптотически приближается к кривой мрачного жнеца (описанной ниже) по мере сжатия. Когда петля схлопывается до сингулярности, общая абсолютная кривизна теряется как минимум 2 π или точно π . [29]
О римановых многообразиях [ править ]
На римановом многообразии любая гладкая простая замкнутая кривая будет оставаться гладкой и простой по мере развития, как и в евклидовом случае. Он либо схлопнется до точки за конечный промежуток времени, либо навсегда останется гладким и простым. В последнем случае кривая обязательно сходится к замкнутой геодезической поверхности. [30]
Погруженные кривые на римановых многообразиях с конечным числом самопересечений становятся самокасающимися только в дискретный набор моментов времени, в каждый из которых они теряют пересечение. Как следствие, количество точек самопересечения не увеличивается. [31]
Сокращение кривой на сфере можно использовать как часть доказательства теоремы о теннисном мячике . Эта теорема утверждает, что каждая гладкая простая замкнутая кривая на сфере, которая делит поверхность сферы на две равные области (как шов теннисного мяча ), должна иметь как минимум четыре точки перегиба . Доказательство основано на наблюдении, что сокращение кривой сохраняет свойства гладкости и деления площади пополам, а не увеличивает количество точек перегиба. Следовательно, это позволяет свести проблему к проблеме для кривых, близких к предельной форме сокращения кривой - большому кругу . [32]
Формула монотонности Хьюскена [ править ]
Согласно формуле монотонности Хьюскена , свертка развивающейся кривой с обращенным во времени тепловым ядром не возрастает. Этот результат можно использовать для анализа особенностей эволюции. [33]
Конкретные кривые [ править ]
Кривые с автомодельной эволюцией [ править ]
Поскольку любая другая простая замкнутая кривая сходится к окружности, окружность - единственная простая замкнутая кривая, которая сохраняет свою форму в потоке сокращения кривой. Однако есть много других примеров кривых, которые либо непростые (они включают самопересечения), либо незамкнутые (они простираются до бесконечности) и сохраняют свою форму. В частности, [34]
- Каждая линия остается неизменной из-за укорачивающего кривую потока. Линии - единственные кривые, на которые не влияет поток укорачивания кривых [34], хотя существуют более сложные устойчивые сети кривых, такие как шестиугольная мозаика плоскости.
- Мрачные кривая жатки у = - лог совы х двигаются вверх без изменения его формы. Таким же образом, любая кривая похожа на Косой будет переведен с помощью кривой укорачиванию потока, сдвинуты в направлении оси симметрии кривой без изменения его формы или ориентации. Мрачный жнец - единственная кривая с этим свойством. [34] В физической литературе ее еще называют шпилькой . [35]
- Семейство самопересекающихся замкнутых кривых, полученных из проекций торических узлов , гомотетически сжимаются, но остаются самоподобными в потоке сокращения кривых. [34] Они стали известны как кривые Абреша – Лангера после работы Абреша и Лангера (1986) , [36] хотя ранее были упомянуты Маллинсом (1956) и независимо открыты Эпштейном и Вайнштейном (1987). . Эти кривые являются локально выпуклыми, поэтому их можно описать опорными функциями . Соответствующим образом масштабированные версии этих опорных функций подчиняются дифференциальному уравнению
- который имеет положительные периодические решения (соответствующие кривым с автомодельной эволюцией) для любого периода, который находится строго между π и . [36]
- Другие кривые, включая некоторые бесконечные спирали , остаются самоподобными с более сложными движениями, включая вращение или комбинации вращения, сжатия или расширения и перемещения. [34]
- Для сетей гладких кривых, встречающихся тройками на стыках с углами 2 π / 3, самоподобные сжимающиеся решения включают двойной пузырь, окружающий две равные области, форму линзы ( vesica piscis ), ограниченную двумя конгруэнтными дугами окружностей вместе с два коллинеарных луча, вершины которых находятся в углах линзы, и сеть «в форме рыбы», ограниченная отрезком прямой, двумя лучами и выпуклой кривой. Любые другие самоподобные усадочные сети включают большее количество кривых. [37] Другое семейство сетей растет гомотетически и остается самоподобным; это древовидные сети кривых, пересекающихся под углами 2 π / 3 в тройных стыках, асимптотическиев веер из двух или более лучей, которые встречаются в общей конечной точке. Двухлучевой случай этих форм представляет собой неограниченную гладкую кривую; для трех или более лучей эволюция этих форм может быть определена с использованием обобщенных вариантов потока укорачивания кривой, таких как вариант для варифолдов. Данный веер из четырех или более лучей может быть асимптотическим для более чем одного решения этого типа, поэтому эти решения не обеспечивают однозначного определения потока, укорачивающего кривую, начинающегося с веера лучей. [38]
Древние решения [ править ]
Древнее решение к задаче потока является кривым, эволюция которой может быть экстраполирована назад на все время, без особенностей. Все самоподобные решения, которые сжимаются или остаются того же размера, а не растут, в этом смысле являются древними; они могут быть экстраполированы назад, обращая преобразование самоподобия, которое они претерпели бы при прямом потоке сокращения кривой. Так, например, круг, мрачный жнец и кривые Абреша – Лангера - все это древние решения. [39]
Единственные замкнутые кривые, кроме круга и кривых Абреша – Лангера, которые образуют древние решения, - это класс кривых, названный Angenent овалами после работы Angenent (1992) . [39] Эти кривые можно параметризовать, указав их кривизну как функцию касательного угла по формуле
и имеют в качестве своей предельной формы при обратной эволюции пару мрачных изгибов жнеца, приближающихся друг к другу с противоположных направлений. [40] В декартовой системе координат они могут быть заданы неявным уравнением кривой [41]
В физической литературе такие же формы известны как модель скрепки . [35]
Для более общих классов кривых, таких как графики функций, известен более разнообразный набор древних решений. [42]
Численные приближения [ править ]
Чтобы эффективно вычислить поток сокращения кривой, как непрерывную кривую, так и непрерывную эволюцию кривой необходимо заменить дискретным приближением.
Переднее отслеживание [ править ]
Методы отслеживания фронта давно используются в гидродинамике для моделирования и отслеживания движения границ между различными материалами, крутых градиентов свойств материала, таких как погодные фронты , или ударных волн внутри одного материала. Эти методы включают вывод уравнений движения границы и их использование для непосредственного моделирования движения границы, а не моделирование подстилающей жидкости и рассмотрение границы как возникающего свойства жидкости. [43] Те же методы можно использовать для моделирования течения, укорачивающего кривую, даже если кривая, претерпевающая поток, не является границей или скачком уплотнения.
В методах отслеживания фронта для сокращения кривой кривая, претерпевающая эволюцию, дискретизируется в виде многоугольника. Метод конечных разностей используется для вывода формул для приближенного вектора нормали и кривизны в каждой вершине многоугольника, и эти значения используются для определения того, как перемещать каждую вершину на каждом временном шаге. [44]Хотя поток сокращения кривой определяется движением кривой перпендикулярно самой себе, некоторые параметризации потока сокращения кривой могут позволить вершинам, которые аппроксимируют кривую, двигаться неперпендикулярно. Фактически, это позволяет вершинам перемещаться по кривой по мере ее развития. Выбор тщательной повторной параметризации может помочь более равномерно перераспределить вершины вдоль кривой в ситуациях, когда перпендикулярное движение может привести к их объединению. [45] Мерриман, Бенс и Ошер (1992) пишут, что эти методы быстрые и точные, но гораздо сложнее расширить их до версий потока сокращения кривой, которые применяются к более сложным входным данным, чем простые замкнутые кривые, где необходимо разобраться с особенностями и изменениями топологии.
Для большинства таких методов Цао (2003) предупреждает, что «условия стабильности не могут быть легко определены, и временной шаг должен выбираться специально». [46] Другой метод конечных разностей, разработанный Crandall & Lions (1996), изменяет формулу для кривизны в каждой вершине, добавляя к ней небольшой член, основанный на операторе Лапласа . Эта модификация называется эллиптической регуляризацией , и ее можно использовать для доказательства существования обобщенных потоков, а также при их численном моделировании. [47] Используя его, можно доказать, что метод Крэндалла и Лайонса сходится, и это единственный численный метод, указанный Цао, который имеет ограничения на скорость его сходимости. [48]Для эмпирического сравнения прямого метода Эйлера , обратного Эйлера и более точных методов конечных разностей Кранка – Николсона см. Balažovjech & Mikula (2009) .
Свертка с повторной дискретизацией [ править ]
Мохтариан и Макворт (1992) предлагают численный метод для вычисления приближения к потоку сокращения кривой, который поддерживает дискретное приближение к кривой и чередует два шага:
- Выполните повторную выборку текущей кривой, разместив новые точки выборки на одинаковом расстоянии, измеренном по нормализованной длине дуги.
- Сверните положения точек с помощью функции Гаусса с небольшим стандартным отклонением, фактически заменяя местоположение каждой точки средневзвешенным значением местоположения ближайших точек вдоль кривой с гауссовыми весами. Стандартное отклонение Гаусса должно быть выбрано достаточно малым, чтобы после этого шага точки выборки все еще имели почти равномерный интервал.
Как они показывают, этот метод сходится к распределению укорачивания кривой в пределе, когда количество точек выборки растет, а нормализованная длина дуги радиуса свертки уменьшается. [49]
Медианная фильтрация [ править ]
Мерриман, Бенце и Ошер (1992) описывают схему, работающую на двумерной квадратной сетке - фактически массив пикселей . Кривая, которая должна развиваться, представлена путем присвоения значения 0 (черный) пикселям, находящимся за пределами кривой, и 1 (белый) пикселям, расположенным внутри кривой, что дает индикаторную функцию для внутренней части кривой. Это представление обновляется путем чередования двух шагов:
- Сверните пиксельное изображение с тепловым ядром, чтобы смоделировать его эволюцию в соответствии с уравнением теплопроводности за короткий временной шаг. Результатом является размытие изображения по Гауссу или, что то же самое, преобразование Вейерштрасса индикаторной функции с радиусом, пропорциональным квадратному корню из временного шага.
- Установите каждый пиксель с числовым значением от 1/2 до 0 и каждый пиксель с числовым значением от 1/2 до 1, вернув изображение к исходным значениям в новых позициях.
Чтобы эта схема была точной, временной шаг должен быть достаточно большим, чтобы кривая сместилась хотя бы на один пиксель даже в точках с низкой кривизной, но достаточно малым, чтобы радиус размытия был меньше минимального радиуса. кривизны. Следовательно, размер пикселя должен быть O (min κ / max κ 2 ) , достаточно малым, чтобы можно было выбрать подходящий промежуточный временной шаг.
Метод может быть обобщен на эволюцию сетей кривых, пересекающихся на стыках и разделяющих плоскость более чем на три области, путем одновременного применения одного и того же метода к каждой области. [50] Вместо размытия и определения порога этот метод можно альтернативно описать как применение медианного фильтра с гауссовыми весами к каждому пикселю. Можно использовать ядра, отличные от теплового ядра, или адаптивно уточнять сетку, чтобы она имела высокое разрешение около кривой, но не тратила время и память на пиксели, далекие от кривой, которые не влияют на результат. [51]Вместо использования только двух значений в пиксельном изображении версия этого метода, в которой используется изображение, значения пикселей которого представляют собой знаковое расстояние до кривой, может достичь субпиксельной точности и потребовать более низкого разрешения. [52]
Приложения [ править ]
Отжиг металлических листов [ править ]
Раннее упоминание Уильяма В. Маллинза ( 1956 ) об укорачивании кривой потока мотивирует его как модель физического процесса отжига , при котором термообработка вызывает смещение границ между зернами кристаллизованного металла. В отличие от мыльных пленок , которые из-за разницы в давлении воздуха становятся поверхностями постоянной средней кривизны., границы зерен при отжиге подвержены только локальным эффектам, которые заставляют их перемещаться согласно потоку средней кривизны. Одномерный случай этого потока, поток с укорачиванием кривой, соответствует листам отжига металла, которые достаточно тонкие, чтобы зерна стали фактически двумерными, а их границы - одномерными. [53]
Анализ формы [ править ]
В обработке изображений и компьютерное зрение , Mokhtarian & Макворт (1992) предлагает применять кривую укорачиванию поток к контуру формы , полученной из цифрового изображения, для того , чтобы удалить шум от формы и обеспечить масштабное пространство , что обеспечивает упрощенное описание формы на разных уровнях разрешения. Метод Мохтариана и Макворта предполагает вычисление потока, сокращающего кривую, с отслеживанием точек перегиба.кривой по мере их прохождения через поток и построение графика, на котором показано положение точек перегиба на кривой в зависимости от параметра времени. Точки перегиба обычно удаляются с кривой попарно, когда кривая становится выпуклой (в соответствии с теоремой Гейджа – Гамильтона – Грейсона), а время жизни пары точек соответствует заметности особенности формы. Из-за метода свертки с повторной выборкой, который они описывают для вычисления численного приближения потока сокращения кривой, они называют свой метод масштабным пространством с повторной выборкой кривизны.. Они отмечают, что это масштабное пространство инвариантно относительно евклидовых преобразований данной формы, и утверждают, что оно однозначно определяет форму и устойчиво к небольшим изменениям формы. Они сравнивают его экспериментально с несколькими связанными альтернативными определениями масштабного пространства для форм и обнаруживают, что масштабное пространство кривизны после повторной дискретизации менее требовательно к вычислениям, более устойчиво к неравномерному шуму и менее сильно зависит от мелкомасштабных различий форм.
Реакция – диффузия [ править ]
В реакционно-диффузионных системах, моделируемых уравнением Аллена-Кана , предельное поведение для быстрой реакции, медленной диффузии и двух или более локальных минимумов энергии с одинаковым энергетическим уровнем друг у друга приводит к тому, что система оседает в областях с разными локальными значениями. минимумы, причем фронты, ограничивающие границы между этими областями, эволюционируют в соответствии с потоком, сокращающим кривую. [54]
Клеточные автоматы [ править ]
В клеточном автомате каждая ячейка в бесконечной сетке ячеек может иметь одно из конечного набора состояний, и все ячейки обновляют свои состояния одновременно, основываясь только на конфигурации небольшого набора соседних ячеек. Жизнь-как клеточный автомат правило является один , в котором сетка является бесконечной квадратной решеткой, существует ровно два состояния ячейки, множество соседей каждой ячейки восемь соседей по соседству Мура, и правило обновления зависит только от количества соседей с каждым из двух состояний, а не от какой-либо более сложной функции этих состояний. В одном конкретном жизненном правиле, введенном Джерардом Вичниаком и называемом правилом скрученного большинства или правилом отжига, правило обновления устанавливает новое значение для каждой ячейки как большинство среди девяти ячеек, заданных ею и ее восемью соседями, за исключением случаев, когда эти ячейки делятся на четыре с одним состоянием и пять с другим состоянием, и в этом случае новое значение ячейки является меньшинством, а не большинством. Детальная динамика этого правила сложна, включая существование небольших стабильных структур. [55]Однако в совокупности (при запуске со всеми ячейками в случайных состояниях) он имеет тенденцию формировать большие области ячеек, которые все находятся в том же состоянии, что и друг друга, причем границы между этими областями развиваются в соответствии с потоком сокращения кривой. [56]
Строительство замкнутых геодезических [ править ]
Поток сокращения кривой можно использовать для доказательства изопериметрического неравенства для поверхностей, гауссова кривизна которых является невозрастающей функцией расстояния от начала координат , таких как параболоид . На такой поверхности гладкий компакт, который имеет любую заданную площадь и минимальный периметр для этой области, обязательно представляет собой круг с центром в начале координат. Доказательство применяет поток сокращения кривой к двум кривым, метрической окружности и границе любого другого компакта и сравнивает изменение периметра двух кривых, поскольку они обе сводятся к точке потоком. [57] Поток сокращения кривой также можно использовать для доказательства теоремы о трех геодезических, что каждое гладкое риманово многообразие, топологически эквивалентное сфере, имеет три геодезические, образующие простые замкнутые кривые . [58]
Связанные потоки [ править ]
К другим геометрическим потокам, связанным с потоком сокращения кривой, относятся следующие.
- Для моделирования поведения кристаллов или других анизотропных материалов важно иметь варианты течения с сокращением кривой, для которых скорость потока зависит от ориентации кривой, а также от ее кривизны. Один из способов сделать это - определить энергию кривой как интеграл от гладкой функции γ ее нормальных векторов и сформировать градиентный поток этой энергии, согласно которому нормальная скорость, с которой течет кривая, пропорциональна анизотропный аналог кривизны. Этот поток можно смоделировать, дискретизируя кривую в виде многоугольника. В численных экспериментах кажется, что исходные кривые сходятся к форме Вульфа для γ, прежде чем сузиться до точки.[59] В качестве альтернативы, можно позволить кривой течь со скоростью a ( θ ) κ + b ( θ ), где κ - (обычная) кривизна, а a и b - гладкие функции ориентации θ . Когда a ( θ + π ) = a ( θ ) и b ( θ + π ) = - b ( θ ) (так что поток инвариантен относительно точечного отражения), можно показать, что результирующий поток подчиняется принципу избегания и аналогу теоремы Гейджа – Гамильтона – Грейсона. [60]
- Поток аффинного сокращения кривой был впервые исследован Альваресом и др. (1993) и Сапиро и Танненбаум (1993) . В этом потоке нормальная скорость кривой пропорциональна кубическому корню из кривизны. [61] Результирующий поток инвариантен (с соответствующим масштабированием по времени) относительно аффинных преобразований евклидовой плоскости, большей группы симметрии, чем преобразования подобия, при которых инвариантен поток, сокращающий кривую. В рамках этого потока применяется аналог теоремы Гейджа – Гамильтона – Грейсона, согласно которому любая простая замкнутая кривая в конечном итоге становится выпуклой, а затем сходится к эллипсукак он схлопывается в точку. [62]
- Преобразование кривой с равными нормальными скоростями во всех точках называется преобразованием травы . Кривые, образованные таким образом, обычно образуют острые углы, след которых образует среднюю ось кривой. [63] Тесно связанная эволюция кривой, которая перемещает прямые сегменты многоугольной кривой с равной скоростью, но позволяет вогнутым углам двигаться быстрее, чем единичная скорость, вместо этого формирует другой тип топологического каркаса данной кривой, ее прямой каркас . [64]
- Для поверхностей в более высоких измерениях существует более одного определения кривизны, включая внешние (зависящие от внедрения) меры, такие как средняя кривизна, и внутренние меры, такие как скалярная кривизна и кривизна Риччи . Соответственно, существует несколько способов определения геометрических потоков на основе кривизны, включая поток средней кривизны (в котором нормальная скорость вложенной поверхности является ее средней кривизной), поток Риччи (собственный поток на основе метрики пространства на основе кривизна Риччи), поток кривизны Гаусса и поток Уиллмора(градиентный поток для функционала энергии, сочетающий среднюю кривизну и гауссову кривизну). Поток сокращения кривой является частным случаем потока средней кривизны и потока кривизны Гаусса для одномерных кривых. [18]
- Вдохновленные потоком сокращения кривой на гладких кривых, исследователи изучили методы плавных многоугольников, чтобы они оставались многоугольными, с приложениями, включая формирование узоров и синхронизацию в распределенных системах роботов. [65] Сохраняющие длину многоугольные потоки можно использовать для решения проблемы правила плотника . [66]
- В области компьютерного зрения , то активная модель контура для обнаружения края и сегментации изображений основана на кривом укорочении и эволюционируют кривые на основе сочетания их кривизны и особенности изображения. [67]
Примечания [ править ]
- ^ Фраза «геометрический тепловой поток» также использовалась для потоков на объектах других типов, кроме кривых, таких как дифференциальные формы .
- ^ Devadoss & O'Rourke (2011) , стр.140: «геометрический поток [является] эволюцией геометрии C во времени t ».
- ^ Devadoss & О'Рурк (2011) , стр. 140.
- ^ a b Грейсон (1989a) .
- ^ Грейсон (1989a) ; Белый (2002) .
- ^ Angenent (1991a) ; Альтшулер и Грейсон (1992) .
- ^ Лауэр (2013) .
- ^ Лам и Лауэр (2016) .
- ^ Ritoré & Sinestrari (2010) , стр. 72.
- ^ Альтшулер (1991) .
- ^ Альтшулер и Грейсон (1992) .
- ^ Бракке (1978) ; Белый (1989) ; Цао (2003) , "4.7.1 Варифолд Бракке", стр. 100. Лауэр (2013) .
- ^ Ilmanen, Neves & Schulze (2014) .
- ↑ White (2002) , стр. 526.
- ↑ White (2002) , стр. 527.
- Перейти ↑ Chou & Zhu (2001) , p. vii; Уайт (2002) , стр. 526.
- ^ Brakke (1978) , Приложение B, предложение 1, стр. 230; Чоу и Чжу (2001) , стр. vii; Уайт (2002) , теорема 1, с. 527.
- ^ а б Уайт (1989) .
- Перейти ↑ Bryant & Griffiths (1995) .
- Перейти ↑ Kimmel (2004) , pp. 182–183.
- ^ Brook, Bruckstein & Kimmel (2005) .
- ^ Цао (2003) , стр. 143.
- ^ Brakke (1978) , Приложение B, предложение 2, стр. 230; Чоу и Чжу (2001) , лемма 5.5, с. 130; «6.1 Уменьшение общей абсолютной кривизны», стр. 144–147.
- Перейти ↑ Chou & Zhu (2001) , p. vii; Уайт (2002) , теоремы 2 и 3, стр. 527–528; Цао (2003) , теорема 3.26, с. 47; Девадосс и О'Рурк (2011) , стр. 141.
- Перейти ↑ Chou & Zhu (2001) , p. vii; Цао (2003) , стр. 47; Девадосс и О'Рурк (2011) , стр. 141.
- Перейти ↑ Chou & Zhu (1998) .
- ^ Ишимура (1995) .
- ^ Шнюрер и др. (2011) ; Беллеттини и Новага (2011) .
- ^ Angenent (1991b) .
- ^ Грейсон (1989b) ; Уайт (2002) , стр. 528; Риторе и Синестрари (2010) , теорема 2.2.1, стр. 73. Этот результат был уже сформулирован как гипотеза по Gage & Hamilton (1986) .
- ^ Angenent (1991a) .
- ^ Angenent (1999) .
- ^ Huisken (1990) .
- ^ а б в г д Маллинз (1956) ; Абреш и Лангер (1986) ; Эпштейн и Вайнштейн (1987) ; Chou & Zhu (2001) , "2. Инвариантные решения для потока, укорачивающего кривую", стр. 27–44; Халлдорссон (2012) ; Altschuler et al. (2013) .
- ^ а б Лукьянов, Витчев и Замолодчиков (2004) ; Huisken & Sinestrari (2015) .
- ^ а б Au (2010) .
- ^ Шнюрер и др. (2011) .
- ↑ Двухлучевой случай уже описан Маллинсом (1956) . Обобщение на два или более лучей и вопросы неединственности см. В Brakke (1978) , приложение C, стр. 235–237, и Ilmanen, Neves & Schulze (2014) .
- ^ а б Даскалопулос, Гамильтон и Сезум (2010) .
- ^ Angenent (1992) .
- ^ Бродбридж & Vassiliou (2011) .
- ^ Вы (2014) .
- ^ См., Например, Scriven (1960) ; Холден и Райзебро (2015) .
- ^ Мерриман, Бенс и Ошер (1992) ; Микула и Шевчович (1999) ; Цао (2003) , "5.1.1 Конечно-разностные методы", стр. 107–108.
- ^ Кимура (1994) ; Декельник и Дзюк (1995) ; Микула и Шевчович (2001) ; Барретт, Гарке и Нюрнберг (2011) ; Эллиотт и Фриц (2017) .
- ^ Цао (2003) , «5.1.1 Конечно-разностные методы», стр. 107–108.
- ^ Ilmanen (1994) , стр. 1 .
- ^ Crandall & Lions (1996) ; Декельник (2000) ; Цао (2003) , "5.2.3 Монотонная и сходящаяся разностные схемы", стр. 109.
- ^ Mokhtarian & Макворт (1992) , стр 796-797. Цао (2003) , стр. 10–11.
- ↑ Merriman, Bence & Osher (1992) .
- ↑ Cao (2003) , «5.2.4 Схема Бенса, Мерримана и Ошера для движения средней кривизны», стр. 109–110. Информацию о корректности медианной фильтрации с другими изотропными ядрами см. В разделе 4.4.1, стр. 90–92.
- ^ Esedoḡlu, Ruuth & Tsai (2010) .
- ↑ Mullins (1956) ; Райнс, Крейг и ДеХофф (1974) ; Бракке (1978) , Приложение А, стр. 224–228.
- Перейти ↑ Rubinstein, Sternberg & Keller (1989) .
- ^ Пиковер (1993) .
- ^ Vichniac (1986) ; Chopard & Droz (1998) .
- ↑ Бенджамини и Цао (1996) ; Риторе и Синестрари (2010) , теорема 2.3.1, стр. 75.
- ^ Грейсон (1989b) .
- ^ Dziuk (1999) ; Хаусер и Фойгт (2006) .
- ^ Chou & Zhu (2001) , глава 6: Класс невыпуклые анизотропных потоков, С. 143-177..
- ^ Цао (2003) , «3.2.3 Аффинный инвариантный поток: простейший аффинный инвариантный поток кривой», стр. 42–46.
- ^ Angenent, Sapiro & Танненбаум (1998) ; Цао (2003) , теорема 3.28, с. 47.
- ^ Сапиро и Танненбаум (1993) .
- ^ Aichholzer et al. (1995) .
- ^ Смит, Брук и Фрэнсис (2007) .
- ^ Cantarella et al. (2004) .
- ^ Kichenassamy et al. (1995) .
Ссылки [ править ]
- Abresch, U .; Лангер, J. (1986), "Нормированный поток кривого укорочения и гомотетические решения", Журнал дифференциальной геометрии , 23 (2): 175-196, DOI : 10,4310 / Jdg / 1214440025 , МР 0845704.
- Айхольцер, Освин; Ауренхаммер, Франц ; Альбертс, Дэвид; Гертнер, Бернд (1995), "Новый тип каркаса для полигонов" , журнал Юниверсал Computer Science , 1 (12): 752-761, CiteSeerX 10.1.1.135.9800 , DOI : 10.1007 / 978-3-642-80350 -5_65 , Руководство по ремонту 1392429.
- Альтшулер, Стивен Дж (1991), "Особенности кривой усадки потока для пространственных кривых", Журнал дифференциальной геометрии , 34 (2): 491-514, DOI : 10,4310 / Jdg / 1214447218 , МР 1131441.
- Альтшулер, Дилан Дж .; Альтшулер, Стивен Дж .; Ангенент, Сигурд Б .; Ву, Лани Ф. (2013), «Зоопарк солитонов для сокращения кривой в », Нелинейность , 26 (5): 1189–1226, arXiv : 1207.4051 , Bibcode : 2013Nonli..26.1189A , doi : 10.1088 / 0951-7715 / 26/5/1189 , MR 3043378 .
- Альтшулер, Стивен Дж .; Грейсон, Мэтью А. (1992), "Укорачивание пространственных кривых и поток через особенности", Журнал дифференциальной геометрии , 35 (2): 283-298, DOI : 10,4310 / Jdg / 1214448076 , МР 1158337.
- Альварес, Луис; Гишар, Фредерик; Львов, Пьер-Луи; Морель, Жан-Мишель (1993), «Аксиомы и фундаментальные уравнения обработки изображений», Архив рациональной механики и анализа , 123 (3): 199–257, Bibcode : 1993ArRMA.123..199A , doi : 10.1007 / BF00375127 , Руководство по ремонту 1225209.
- Эндрюс, Бен; Брайан, Пол (2011), «Оценка кривизны для потока, укорачивающего кривую, посредством сравнения расстояний и прямого доказательства теоремы Грейсона», Journal für die Reine und Angewandte Mathematik , 2011 (653): 179–187, arXiv : 0908.2682 , doi : 10.1515 /CRELLE.2011.026 , Руководство по эксплуатации 2794630.
- Angenent, Sigurd (1991a), "Параболические уравнения для кривых на поверхностях. II. Пересечения, разрушение и обобщенные решения", Annals of Mathematics , Second Series, 133 (1): 171–215, doi : 10.2307 / 2944327 , JSTOR 2944327 , MR 1087347.
- Angenent, Сигурд (1991b), "О формировании особенностей в потоке укорочения кривой", Журнал дифференциальной геометрии , 33 (3): 601-633, DOI : 10.4310 / JDG / 1214446558 , MR 1100205.
- Angenent, Sigurd B. (1992), "Shrinking donuts" (PDF) , Нелинейные уравнения диффузии и их состояния равновесия, 3 (Gregynog, 1989) , Progress in Nonlinear Differential Equations and their Applications, 7 , Boston, MA: Birkhäuser, pp. 21–38, MR 1167827.
- Angenent, S. (1999), «Точки перегиба, экстатические точки и укорочение кривой» (PDF) , Гамильтоновы системы с тремя или более степенями свободы (S'Agaró, 1995) , NATO Adv. Sci. Inst. Сер. C Math. Phys. Sci., 533 , Dordrecht: Kluwer Acad. Publ., Pp. 3–10, MR 1720878.
- Ангенент, Сигурд ; Сапиро, Гильермо ; Танненбаум, Аллен (1998), "О аффинном уравнении теплопроводности для не-выпуклых кривых", Журнал Американского математического общества , 11 (3): 601-634, DOI : 10,1090 / S0894-0347-98-00262-8 , Руководство по ремонту 1491538.
- Ау, Томас Квок-Кеунг (2010), "Свойство седловой точки кривых Абреша-Лангера под потоком сокращения кривой", Коммуникации в области анализа и геометрии , 18 (1): 1–21, arXiv : math / 0102088 , doi : 10.4310 / CAG.2010.v18.n1.a1 , Руководство по ремонту 2660456.
- Балажович, Мартин; Микула, Кароль (2009), "Схема более высокого порядка для кривой, укорачивающей поток плоских кривых" (PDF) , Алгоритмы 2009 , стр. 165–175.
- Барретт, Джон В .; Гарке, Харальд; Nürnberg, Роберт (2011), "О приближении плоской кривой эволюции стабильными полностью неявных схем конечных элементов , что equidistribute" (PDF) , Численные методы для дифференциальных уравнений в частных , 27 : 1-30, DOI : 10.1002 / num.20637 , MR 2743598.
- Беллеттини, Джованни; Новага, Маттео (2011), «Эволюция кривизны невыпуклых линзовидных доменов», Journal für die Reine und Angewandte Mathematik , 2011 (656): 17–46, arXiv : 0906.0166 , doi : 10.1515 / CRELLE.2011.041 , MR 2818854.
- Бенджамини, Итаи ; Као, цзянья (1996), "Новая теорема изопериметрической сравнении для поверхностей переменной кривизны", Герцога математического журнал , 85 (2): 359-396, DOI : 10,1215 / S0012-7094-96-08515-4 , МР 1417620.
- Бракке, Кеннет А. (1978), Движение поверхности по ее средней кривизне (PDF) , Mathematical Notes, 20 , Princeton University Press, Princeton, NJ, ISBN 0-691-08204-9, Руководство по ремонту 0485012.
- Бродбридж, Филип; Василиу, Питер (2011), «Роль симметрии и разделения в эволюции поверхности и сокращении кривой», SIGMA , 7 : Paper 052, 19, arXiv : 1106.0092 , Bibcode : 2011SIGMA ... 7..052B , doi : 10.3842 / СИГМА.2011.052 , Руководство 2804584.
- Брук, Александр; Bruckstein, Альфред М .; Киммел, Рон (2005), «О мерах справедливости, инвариантных к подобию», в Киммел, Рон ; Sochen, Nir A .; Weickert, Joachim (eds.), Scale Space и PDE Methods in Computer Vision: 5th International Conference, Scale-Space 2005, Hofgeismar, Germany, 7–9 апреля 2005 г., Proceedings , Lecture Notes in Computer Science, 3459 , Springer-Verlag ., стр 456-467, CiteSeerX 10.1.1.67.1807 , DOI : 10.1007 / 11408031_39.
- Брайант, Роберт Л .; Гриффитс, Филип А. (1995),, "Характеристика когомология дифференциальных систем II Законы сохранения для одного класса параболических уравнений.." Герцог математический журнал , 78 (3): 531-676, DOI : 10.1215 / S0012-7094-95 -07824-7 , MR 1334205. См., В частности, Пример 1, стр. 542–544 и 601–604.
- Кантарелла, Джейсон Х .; Демейн, Эрик Д .; Ибен, Хейли Н .; О'Брайен, Джеймс Ф. (2004), «Энергетический подход к разворачиванию связей», Труды двадцатого ежегодного симпозиума по вычислительной геометрии (SCG '04) , Нью-Йорк, Нью-Йорк, США: ACM, стр. 134– 143, CiteSeerX 10.1.1.1001.9683 , DOI : 10,1145 / 997817,997840 , ISBN 1-58113-885-7.
- Цао, Фредерик (2003), Эволюция геометрической кривой и обработка изображений , Лекционные заметки по математике, 1805 , Берлин: Springer-Verlag, doi : 10.1007 / b10404 , ISBN 3-540-00402-5, MR 1976551.
- Chopard, Bastien; Дроз, Мишель (1998), "2.2.4 Правило отжига", Моделирование физических систем клеточными автоматами , Коллекция Алеа-Сакле: Монографии и тексты по статистической физике, Cambridge University Press, Кембридж, стр. 37–38, DOI : 10.1017 / CBO9780511549755 , ISBN 0-521-46168-5, MR 1669736.
- Чжоу, Кай-Сен; Чжу Си-пинг (1998), "Укорачивание полных кривые плоскости", Журнал дифференциальной геометрии , 50 (3): 471-504, DOI : 10,4310 / Jdg / 1214424967 , МР 1690737.
- Чжоу, Кай-Сен; Чжу, Си-Пин (2001), Проблема укорочения кривой , Бока-Ратон, Флорида: Чепмен и Холл / CRC, DOI : 10.1201 / 9781420035704 , ISBN 1-58488-213-1, MR 1888641.
- Крэндалл, Майкл Дж .; Львы, Пьер-Луи (1996), "Разностные схемы для нелинейных конвергентные параболических уравнений и движения средней кривизны", Numerische Mathematik , 75 (1): 17-41, DOI : 10.1007 / s002110050228 , МР 1417861.
- Даскалопулос, Панайота ; Гамильтон, Ричард ; Sesum, Наташа (2010), "Классификация компактных древних решений для потока укорочения кривой", Журнал дифференциальной геометрии , 84 (3): 455-464, Arxiv : 0806,1757 , DOI : 10,4310 / Jdg / 1279114297 , МР 2669361.
- Deckelnick, Клаус (2000), "Границы ошибок для разностной схемы , аппроксимирующей решения вязкости среднего потока кривизны", Интерфейсы и свободными границами , 2 (2): 117-142, DOI : 10,4171 / ПУТ / 15 , MR 1760409.
- Deckelnick, K .; Дзюк, Г. (1995), "Об аппроксимации потока сокращения кривой", Вариационное исчисление, приложения и вычисления (Pont-à-Mousson, 1994) , Pitman Res. Notes Math. Сер., 326 , Longman Sci. Tech., Harlow, pp. 100–108, MR 1419337.
- Девадосс, Сатьян Л .; О'Рурк, Джозеф (2011), «5.5 Сокращение кривой», Дискретная и вычислительная геометрия , Принстон, Нью-Джерси: Princeton University Press, стр. 138–144, ISBN 978-0-691-14553-2, Руководство по ремонту 2790764.
- Dziuk, Герхард (1999), "Дискретный анизотропные кривое укорочение поток", SIAM журнал по численному анализу , 36 (6): 1808-1830, DOI : 10,1137 / S0036142998337533 , МР 1712165.
- Эллиотт, Чарльз М .; Фриц, Ханс (2017), «Об аппроксимациях потока укорачивания кривой и потока средней кривизны на основе трюка ДеТурка», Журнал численного анализа IMA , 37 (2): 543–603, arXiv : 1602.07143 , doi : 10.1093 / imanum / drw020 , Руководство по ремонту 3649420.
- Эпштейн, CL ; Вайнштейн, М. (1987), "устойчивое многообразие теоремы для кривого укорочения уравнения", коммуникации по чистой и прикладной математике , 40 (1): 119-139, DOI : 10.1002 / cpa.3160400106 , МР 0865360.
- Эседоглу, Селим; Руут, Стивен; Цай, Ричард (2010), «Движение, генерируемое диффузией с использованием функций расстояния со знаком » (PDF) , Journal of Computational Physics , 229 (4): 1017–1042, Bibcode : 2010JCoPh.229.1017E , doi : 10.1016 / j.jcp.2009.10 .002 , Руководство по ремонту 2576237.
- Гейдж, Michael E. (1983), "Изопериметрическое неравенство с приложениями к кривому укорочению", Герцога математического журнал , 50 (4): 1225-1229, DOI : 10,1215 / S0012-7094-83-05052-4 , МР 0726325.
- Gage, ME (1984), «Укорачивание кривой делает выпуклые кривые круглыми», Inventiones Mathematicae , 76 (2): 357–364, Bibcode : 1984InMat..76..357G , doi : 10.1007 / BF01388602 , MR 0742856.
- Гейдж, М .; Гамильтон, Р. (1986), "Уравнение термоусадки выпуклых кривые плоскости", Журнал дифференциальной геометрии , 23 (1): 69-96, DOI : 10,4310 / Jdg / 1214439902 , МР 0840401.
- Грейсон, Мэтью А. (1987), "Уравнение теплопроводности психиатры встроенная плоские кривые для круглых точек", Журнал дифференциальной геометрии , 26 (2): 285-314, DOI : 10,4310 / Jdg / 1214441371 , МР 0906392.
- Грейсон, Мэтью А. (1989a), "Форма восьмерки под потоком сокращения кривой" , Inventiones Mathematicae , 96 (1): 177–180, Bibcode : 1989InMat..96..177G , doi : 10.1007 / BF01393973 , Руководство по ремонту 0981740.
- Грейсон, Мэтью А. (1989b), "Укорачивание встроенных кривых" (PDF) , Анналы математики , вторая серия, 129 (1): 71-111, DOI : 10,2307 / 1971486 , JSTOR 1971486 , МР 0979601.
- Халлдорссон, Хёскулдур П. (2012), «Автомодельные решения для потока сокращения кривой», Труды Американского математического общества , 364 (10): 5285–5309, arXiv : 1007.1617 , doi : 10.1090 / S0002-9947-2012 -05632-7 , Руководство по ремонту 2931330.
- Хаусер, Франк; Фойгт, Axel (2006), "Численный схема регуляризованное анизотропного потока кривой укорочения", Applied Mathematics Letters , 19 (8): 691-698, DOI : 10.1016 / j.aml.2005.05.011 , MR 2232241.
- Холден, Хельге; Райзебро, Нильс Хенрик (2015), Отслеживание фронта для гиперболических законов сохранения , Прикладные математические науки, 152 (2-е изд.), Springer, ISBN 978-3-662-47507-2.
- Huisken, Герхард (1990), "Асимптотика для особенностей среднего потока кривизны", Журнал дифференциальной геометрии , 31 (1): 285-299, DOI : 10,4310 / Jdg / 1214444099 , МР 1030675.
- Huisken, Герхард (1998), "Принцип сравнения расстояния для эволюции кривых", Азиатский журнал математики , 2 (1): 127-133, DOI : 10,4310 / ajm.1998.v2.n1.a2 , МР 1656553.
- Huisken, Герхард ; Синестрари, Карло (2015), «Выпуклые древние решения потока средней кривизны», Журнал дифференциальной геометрии , 101 (2): 267–287, arXiv : 1405.7509 , doi : 10.4310 / jdg / 1442364652 , MR 3399098.
- Ильманен, Том (1994), "Эллиптическая регуляризация и частичная регулярность движения по средней кривизне", Мемуары Американского математического общества , 108 (520), DOI : 10.1090 / memo / 0520 , MR 1196160.
- Ильманен, Том; Невес, Андре ; Шульце, Феликс (2014), О кратковременном существовании плоского сетевого потока , arXiv : 1407.4756 , Bibcode : 2014arXiv1407.4756I.
- Ишимура, Наойуки (1995), "Кривизна эволюция плоских кривых с заданным углом раскрытия", Бюллетень австралийского математического общества , 52 (2): 287-296, DOI : 10,1017 / S0004972700014714 , МР 1348488.
- Kichenassamy, S .; Кумар, А .; Olver, P .; Танненбаум, А .; Еззи, А. (1995), "Градиентные потоки и геометрические модели активного контура", Труды Международной конференции IEEE по компьютерному зрению , стр. 810–815, CiteSeerX 10.1.1.331.6675 , doi : 10.1109 / iccv.1995.466855.
- Киммел, Рон (2004), Численная геометрия изображений: теория, алгоритмы и приложения , Springer-Verlag, ISBN 978-0-387-21637-9, MR 2028182.
- Кимура, М. (1994), "Точная численная схема для потока с помощью кривизны", Прикладная Математика Письма , 7 (1): 69-73, DOI : 10,1016 / 0893-9659 (94) 90056-6 , МР 1349897.
- Лам, Кейси; Лауэр, Джозеф (2016), Заданный уровень синусоидальной кривой тополога является плавным , arXiv : 1601.02442 , Bibcode : 2016arXiv160102442L
- Лауэр, Джозеф (2013), «Новая оценка длины для потока сокращения кривой и исходных данных с низкой регулярностью», Геометрический и функциональный анализ , 23 (6): 1934–1961, arXiv : 1102.5110 , doi : 10.1007 / s00039-013-0248 -1 , Руководство MR 3132906.
- Лукьянов, С.Л .; Витчев Е.С.; Замолодчиков, А.Б. (2004), «Интегрируемая модель граничного взаимодействия: скрепка», Nuclear Physics B , 683 (3): 423–454, arXiv : hep-th / 0312168 , Bibcode : 2004NuPhB.683..423L , doi : 10.1016 / j.nuclphysb.2004.02.010.
- Мерриман, Барри; Бенс, Джеймс; Ошер, Стэнли (апрель 1992 г.), Движение, вызванное диффузией по средней кривизне (PDF) , Отчет CAM 92-18, Департамент математики, Калифорнийский университет, Лос-Анджелес. Также опубликовано в Taylor, Jean E. (1992), Computational Crystal Growers Workshop: Proceedings of the Geometry Center Workshop, проводившемся в Миннеаполисе, Миннесота, 22–28 февраля 1992 г. , Selected Lectures in Mathematics, Providence, RI: American Mathematical Society, стр. 73–83, ISBN 0-8218-8072-1, Руководство по ремонту 1224451.
- Микула, Кароль; Ševčovič, Дэниел (1999), "Решение нелинейна кривизна привода эволюции плоских кривых", Прикладная вычислительная математика , 31 (2): 191-207, DOI : 10.1016 / S0168-9274 (98) 00130-5 , МР 1708959.
- Микула, Кароль; Шевчович, Даниэль (2001), «Эволюция плоских кривых, обусловленная нелинейной функцией кривизны и анизотропии», SIAM Journal on Applied Mathematics , 61 (5): 1473–1501 (электронный), CiteSeerX 10.1.1.32.1138 , doi : 10.1137 / S0036139999359288 , Руководство по ремонту 1824511.
- Мохтарян, Ф .; Макворт, А. К. (1992), "Теория многомасштабных, представление формы кривизны на основе для плоских кривых" (PDF) , IEEE Transactions на шаблон анализа и Machine Intelligence , 14 (8): 789-805, DOI : 10,1109 / 34,149591.
- Mullins, WW (1956), «Двумерное движение идеализированных границ зерен», Journal of Applied Physics , 27 (8): 900–904, Bibcode : 1956JAP .... 27..900M , doi : 10.1063 / 1.1722511. Перепечатано в Болле, Джон М .; Киндерлерер, Дэвид ; Подио-Гуидугли, Пауло; Slemrod, Marshall, eds. (1999), Фундаментальный вклад в теорию континуума развивающихся фазовых границ в твердых телах: сборник оттисков 14 основных статей , Springer-Verlag, стр. 70–74, DOI : 10.1007 / 978-3-642-59938-5_3 , ISBN 978-3-642-59938-5.
- Пиковер, Clifford A. (1993), "Лава лампы в 21 - м веке", Визуальный Компьютер , 10 (3): 173-177, DOI : 10.1007 / bf01900906.
- Rhines, Frederick N .; Craig, Kenneth R .; ДеХофф, Роберт Т. (1974), «Механизм устойчивого роста зерна в алюминии», Металлургические операции , 5 (2): 413–425, Bibcode : 1974MT ...... 5..413R , doi : 10.1007 / bf02644109.
- Риторе, Мануэль; Синестрари, Карло (2010), «2.2 Поток, сокращающий кривую» , Средняя кривизна потока и изопериметрические неравенства , Продвинутые курсы по математике - CRM Barcelona, Birkhäuser, стр. 72–75, DOI : 10.1007 / 978-3-0346-0213-6_13 , ISBN 978-3-0346-0213-6.
- Рубинштейн, Якоб; Штернберг, Питер; Келлера, Джозеф Б. (1989), "Быстрая реакция, медленная диффузия, а кривое укорочение", SIAM журнал по прикладной математике , 49 (1): 116-133, DOI : 10,1137 / 0149007 , МР 0978829.
- Сапиро, Гильермо ; Танненбаум, Allen (1993), "Аффинная инвариантна масштабно-пространство", Международный журнал Computer Vision , 11 (1): 25-44, DOI : 10.1007 / bf01420591.
- Schnürer, Oliver C .; Азуани, Абдеррахим; Георгий, Марк; Ад, Джульетта! Джангл, Нихар; Келлер, Амос; Марксен, Тобиас; Ритталер, Сандра; Саез, Мариэль; Шульце, Феликс; Смит, Брайан (2011), «Эволюция сетей в форме выпуклых линз под потоком сокращения кривой», Труды Американского математического общества , 363 (5): 2265–2294, arXiv : 0711.1108 , doi : 10.1090 / S0002-9947- 2010-04820-2 , Руководство по ремонту 2763716.
- Скривен, Л. (1960), "Динамика границы раздела жидкостей уравнение движения для ньютоновских жидкостей поверхности", Chemical Engineering Science , 12 (2): 98-108, DOI : 10.1016 / 0009-2509 (60) 87003-0.
- Смит, Стивен Л .; Бруке, Мирей Э .; Фрэнсис, Брюс А. (2007), «Сокращение кривой и проблема рандеву для мобильных автономных роботов», IEEE Transactions on Automatic Control , 52 (6): 1154–1159, arXiv : cs / 0605070 , doi : 10.1109 / tac.2007.899024.
- Vichniac, Gérard Y. (1986), "Модели беспорядка и организации клеточных автоматов", в Bienenstock, E .; Fogelman Soulié, F .; Weisbuch, G. (eds.), Disordered Systems and Biological Organization , NATO ASI Series, 20 , Springer-Verlag, pp. 3–20, doi : 10.1007 / 978-3-642-82657-3_1.
- Белый, Брайан (1989), "Некоторые недавние разработки в области дифференциальной геометрии", Математическая Интеллидженсер , 11 (4): 41-47, DOI : 10.1007 / BF03025885 , МР 1016106.
- Уайт, Брайан (2002), "Эволюция кривых и поверхностей по средней кривизне", Труды Международного конгресса математиков, Vol. I (Пекин, 2002) , Высшее изд. Press, Beijing, pp. 525–538, arXiv : math / 0212407 , Bibcode : 2002math ..... 12407W , MR 1989203.
- Ю, Цянь (2014), Некоторые древние решения сокращения кривой , доктор философии. диссертация, Университет Висконсина - Мэдисон, ProQuest 1641120538 .