Геометрическая серия

Геометрический ряд 1/4 + 1/16 + 1/64 + 1/256 + ... показан в виде областей фиолетовых квадратов. Каждый из фиолетовых квадратов имеет 1/4 площади следующего большего квадрата ( 1/2 × 1/2 = 1/4, 1/4 × 1/4 = 1/16 и т. Д.). Сумма площадей фиолетовых квадратов составляет одну треть площади большого квадрата.

Другой геометрический ряд (коэффициент a = 4/9 и знаменатель r = 1/9) показан в виде областей фиолетовых квадратов. Общая фиолетовая площадь равна S = a / (1 - r ) = (4/9) / (1 - (1/9)) = 1/2, что можно подтвердить, наблюдая, что внешний квадрат разделен на бесконечные количество L-образных областей, каждая с четырьмя фиолетовыми квадратами и четырьмя желтыми квадратами, которые наполовину фиолетовые.

В математике , А геометрический ряд представляет собой сумму бесконечного числа терминов , которые имеют отношение постоянного между последовательными условиями. Например, сериал

${\ displaystyle {\ frac {1} {2}} \, + \, {\ frac {1} {4}} \, + \, {\ frac {1} {8}} \, + \, {\ гидроразрыв {1} {16}} \, + \, \ cdots}$

является геометрическим, потому что каждый последующий член можно получить, умножив предыдущий член на 1/2. Как правило, геометрический ряд записывается как a + ar + ar ² + ar ³ + ..., где a - коэффициент каждого члена, а r - общее отношение между соседними членами. Геометрические ряды являются одними из простейших примеров бесконечных рядов и могут служить основным введением в ряды Тейлора и Фурье . Геометрические ряды сыграли важную роль в раннем развитии математического анализа., используются в математике и имеют важные приложения в физике , инженерии , биологии , экономике , информатике , теории очередей и финансах .

Разница между прогрессией и серией состоит в том, что прогрессия - это последовательность, а серия - это сумма.

Коэффициент а [ править ]

Первые девять членов геометрического ряда 1 + r + r ² + r ³ ... нарисованные как функции (окрашенные в следующем порядке: красный, зеленый, синий, красный, зеленый, синий, ...) в диапазоне -1 < r <1. Замкнутый геометрический ряд 1 / (1 - r ) обозначен черным пунктиром.

Геометрический ряд a + ar + ar ² + ar ³ + ... записан в развернутом виде. ^[1] Все коэффициенты геометрического ряда одинаковы. В противоположность этому , силовые серии записывается как в ₀ + ₁ г + в ₂ г ² + ₃ г ³ + ... в развернутом виде имеет коэффициенты _я , которые могут варьироваться в зависимости от срока до срока. Другими словами, геометрический ряд - это частный случайстепенного ряда. Первый член геометрического ряда в развернутой форме - это коэффициент a этого геометрического ряда.

Помимо развернутой формы геометрического ряда, существует образующая форма ^[2] геометрического ряда, записанная как

${\ Displaystyle \ сумма _ {к = 0} ^ {\ infty}}$ ar ^k

и замкнутый вид геометрического ряда, записанный как

a / (1 - r ) в диапазоне | г | <1.

Вывод закрытой формы из развернутой показан в разделе « Сумма» этой статьи . Для вывода требуется, чтобы все коэффициенты ряда были одинаковыми (коэффициент a), чтобы воспользоваться преимуществом самоподобия и уменьшить бесконечное количество операций сложения и увеличения в расширенной форме до единственного вычитания и единственного деления в закрытая форма. Однако даже без этого вывода результат может быть подтвержден длинным делением : a, деленное на (1 - r ), дает a + ar + ar ² + ar ³ + ..., который является расширенной формой геометрического ряда.

Обычно геометрический ряд рассматривается как сумма чисел a + ar + ar ² + ar ³ + ..., но также может рассматриваться как сумма функций a + ar + ar ² + ar ³ + ..., которые сходится к функции a / (1 - r ) в диапазоне | r | <1. На соседнем изображении показан вклад каждого из первых девяти членов (т. Е. Функций) в функцию a / (1 - r ) в диапазоне | г | <1 , когда= 1. Изменение даже одного из коэффициентов на значение, отличное от коэффициента a, привело бы (в дополнение к изменению геометрического ряда на степенной ряд) к изменению итоговой суммы функций на некоторую функцию, отличную от a / (1 - r ) в пределах диапазона | г | <1. Кроме того, особенно полезное изменение коэффициентов определяется рядом Тейлора , который описывает, как изменить коэффициенты так, чтобы сумма функций сходилась к любой выбранной пользователем достаточно гладкой функции в пределах диапазона.

Общее соотношение r [ править ]

Геометрический ряд a + ar + ar ² + ar ³ + ... представляет собой бесконечный ряд, определяемый всего двумя параметрами : коэффициентом a и знаменателем r . Общий коэффициент r - это отношение любого члена к предыдущему члену в ряду. Или, что то же самое, обычное отношение r - это множитель, используемый для вычисления следующего члена в ряду. В следующей таблице показано несколько геометрических рядов:

Сходимость геометрического ряда зависит от значения знаменателя r :

• Если | г | <1 члены ряда в пределе стремятся к нулю (становятся все меньше и меньше по величине ), и ряд сходится к сумме a / (1 - r ).
• Если | г | = 1, ряд не сходится. Когда r = 1, все члены ряда одинаковы, а серия бесконечна. Когда r = -1, члены принимают два значения поочередно (например, 2, -2, 2, -2, 2, ...). Сумма членов колеблется между двумя значениями (например, 2, 0, 2, 0, 2, ...). Это другой тип расхождения. См., Например , ряд Гранди : 1 - 1 + 1 - 1 + ···.
• Если | г | > 1 члены ряда становятся все больше и больше по величине. Сумма членов также становится все больше и больше, и ряд не сходится к сумме. (Серии расходятся .)

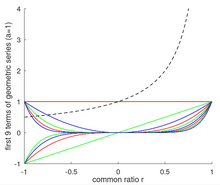
Скорость сходимости также зависит от значения общего коэффициента r . В частности, скорость сходимости снижается, когда r приближается к 1 или -1. Например, геометрический ряд с a = 1 равен 1 + r + r ² + r ³ + ... и сходится к 1 / (1 - r ), когда | г | <1. Однако количество членов, необходимых для сходимости, стремится к бесконечности, когда r приближается к 1, потому что a / (1 - r ) стремится к бесконечности и каждый член ряда меньше или равен единице. Напротив, поскольку rприближается к -1, сумма первых нескольких членов геометрического ряда начинает сходиться к 1/2, но слегка переворачивается вверх или вниз в зависимости от того, имеет ли последний добавленный член степень r , четную или нечетную. Такое поведение переворота около r = −1 показано на соседнем изображении, показывающем первые 11 членов геометрического ряда с a = 1 и | г | <1.

Коэффициент отношения r и коэффициент a также определяют геометрическую прогрессию , которая представляет собой список членов геометрического ряда, но без добавлений. Следовательно, геометрическая последовательность a + ar + ar ² + ar ³ + ... имеет геометрическую прогрессию (также называемую геометрической последовательностью) a , ar , ar ² , ar ³ , ... Геометрическая прогрессия - настолько проста, насколько она есть - моделирует удивительное количество природных явлений ,

• из некоторых крупнейших наблюдений, таких как расширение Вселенной, где общее отношение r определяется постоянной Хаббла ,
• к некоторым из мельчайших наблюдений, таких как распад радиоактивных атомов углерода-14, где обычное отношение r определяется периодом полураспада углерода-14 .

Кроме того, обычное отношение r может быть комплексным числом, например | r | e ^iθ, где | г | представляет собой вектор величина «с (или длиной) и θ представляет угол вектора (или ориентация) в комплексной плоскости . С общим соотношением | r | e ^iθ , развернутая форма геометрического ряда имеет вид a + a | г | е ^iθ + а | г | ² e ^i2θ + a | г | ³ e ^i3θ+ ... Моделируя угол θ как линейно увеличивающийся во времени со скоростью некоторой угловой частоты ω ₀ (другими словами, делая замену θ = ω ₀ t), расширенная форма геометрического ряда принимает вид a + a | r | e ^{iω ₀ t} + a | г | ² e ^{i2ω ₀ t} + a | г | ³ e ^{i3ω ₀ t} + ..., где первое слагаемое - вектор длины aне вращается вообще, а все остальные члены являются векторами разной длины, вращающимися с гармониками основной угловой частоты ω ₀ . Ограничения | r | <1 достаточно, чтобы скоординировать это бесконечное количество векторов разной длины, все вращающиеся с разной скоростью, для отслеживания круга, как показано на соседнем видео. Подобно тому, как ряд Тейлора описывает, как изменять коэффициенты, чтобы ряд сходился к выбранной пользователем достаточно гладкой функции в пределах диапазона, ряд Фурье описывает, как изменять коэффициенты (которые также могут быть комплексными числами, чтобы указать начальные углы векторов), поэтому ряд сходится к периодической функции, выбранной пользователем .

Сумма [ править ]

Формула закрытого типа [ править ]

Действительно , сумма первых n +1 членов геометрического ряда до члена r ⁿ включительно равна${\ displaystyle r \ neq 1}$

${\ displaystyle a + ar + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n} = \ sum _ {k = 0} ^ {n} ar ^ {k} = a \ left ( {\ frac {1-r ^ {n + 1}} {1-r}} \ right),}$

где r - обычное отношение. Эту формулу в замкнутой форме для частичной суммы s можно получить , вычитая множество самоподобных членов следующим образом: ^{[3] [4] [5]}

${\ Displaystyle {\ begin {align} s = a \ + \ & ar \ + \ ar ^ {2} \ + \ ar ^ {3} \ + \ \ cdots \ + \ ar ^ {n}, \\ rs = \ & ar \ + \ ar ^ {2} \ + \ ar ^ {3} \ + \ \ cdots \ + \ ar ^ {n} \ + \ ar ^ {n + 1}, \\ s-rs = \ & a \ - \ ar ^ {n + 1}, \\ s (1-r) = \ & a (1-r ^ {n + 1}), \\ s = \ & a \ left ({\ frac {1-r ^ {n + 1}} {1-r}} \ right) \ quad {\ text {(if}} r \ neq 1 {\ text {)}}. \ end {выравнивается}}}$

Когда n приближается к бесконечности, абсолютное значение r должно быть меньше единицы, чтобы ряд сходился. Тогда сумма станет

${\displaystyle a+ar+ar^{2}+ar^{3}+ar^{4}+\cdots =\sum _{k=0}^{\infty }ar^{k}={\frac {a}{1-r}},{\text{ for }}|r|<1.}$

Когда a = 1 , это можно упростить до

${\displaystyle 1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots \;=\;{\frac {1}{1-r}}.}$

Формула справедлива для комплексного г , с соответствующим ограничением, то модуль из р строго меньше единицы.

Кроме того, вопрос о том, сходится ли бесконечный ряд, по сути, является вопросом о расстоянии между двумя значениями: при достаточном количестве членов становится ли значение частичной суммы сколь угодно близким к значению, к которому оно приближается? В приведенном выше выводе замкнутой формы геометрического ряда интерпретация расстояния между двумя значениями - это расстояние между их положениями на числовой прямой . Это наиболее распространенная интерпретация расстояния между двумя значениями. Однако p-адическая метрика , которая стала критическим понятием в современной теории чисел , предлагает такое определение расстояния, что геометрический ряд 1 + 2 + 4 + 8 + ... с a = 1 и r= 2 действительно сходится к a / (1 - r ) = 1 / (1 - 2) = -1, даже если r находится за пределами типичного диапазона сходимости | г | <1.

Доказательство сходимости [ править ]

Мы можем доказать, что геометрический ряд сходится, используя формулу суммы для геометрической прогрессии :

${\displaystyle {\begin{aligned}1+r+r^{2}+r^{3}+\cdots \ &=\lim _{n\rightarrow \infty }\left(1+r+r^{2}+\cdots +r^{n}\right)\\&=\lim _{n\rightarrow \infty }{\frac {1-r^{n+1}}{1-r}}.\end{aligned}}}$

Поскольку (1 + r + r ² + ... + r ⁿ ) (1− r )

= ((1-r) + (r - r ² ) + ( r ² - r ³ ) + ... + ( r ⁿ - r ^{n + 1} ))

= ((1 -r) + (r - r ² ) + ( r ² - r ³ ) + ... + ( r ⁿ - r ^{n + 1} ))

= 1 - r ^{n +1} и r ^{n +1} → 0 для | г  | <1.

Сходимость геометрических рядов также можно продемонстрировать, переписав ряд как эквивалентный телескопический ряд . Рассмотрим функцию,

${\displaystyle g(K)={\frac {r^{K}}{1-r}}.}$

Обратите внимание, что

${\displaystyle 1=g(0)-g(1)\ ,\ r=g(1)-g(2)\ ,\ r^{2}=g(2)-g(3)\ ,\ldots }$

Таким образом,

${\displaystyle S=1+r+r^{2}+r^{3}+\cdots =(g(0)-g(1))+(g(1)-g(2))+(g(2)-g(3))+\cdots .}$

Если

${\displaystyle |r|<1}$

тогда

${\displaystyle g(K)\longrightarrow 0{\text{ as }}K\to \infty .}$

Итак, S сходится к

${\displaystyle g(0)={\frac {1}{1-r}}.}$

Скорость конвергенции [ править ]

Как показано в приведенных выше доказательствах, замкнутая форма частичной суммы геометрического ряда до n-й степени числа r включительно представляет собой (1 - r ^{n + 1} ) / (1 - r ) для любого значения r , и замкнутая форма геометрического ряда представляет собой полную сумму a / (1 - r ) в диапазоне | г | <1.

Если общее отношение находится в диапазоне 0 < r <1, тогда частичная сумма a (1 - r ^{n + 1} ) / (1 - r ) увеличивается с каждым добавленным членом и в конечном итоге попадает в небольшую ошибку E , отношение полная сумма a / (1 - r ). Решая для n при этом пороге ошибки,

${\displaystyle {\begin{aligned}a\left({\frac {1-r^{n+1}}{1-r}}\right)&\geq a\left({\frac {1-E}{1-r}}\right),\\1-r^{n+1}&\geq 1-E,\\r^{n+1}&\leq E,\\ln(r^{n+1})&\geq ln(E),\\(n+1)ln(r)&\geq ln(E),\\n+1&\geq \left\lceil {\frac {ln(E)}{ln(r)}}\right\rceil ,\end{aligned}}}$

где 0 < r <1, операция потолка ограничивает n целыми числами, а операция натурального логарифма ln переворачивает неравенство, поскольку она отрицает обе стороны неравенства (поскольку обе стороны меньше единицы). Результат n + 1 - это количество членов частичной суммы, необходимое для получения в пределах aE / (1 - r ) полной суммы a / (1 - r ). Например, чтобы получить в пределах 1% от полной суммы a / (1 - r ) при r = 0,1, только 2 (= ln (E) / ln (r) = ln (0,01) / ln (0,1)) слагаемых частичная сумма не требуется. Однако при r = 0,9 необходимо 44 (= ln (0,01) / ln (0,9)) членов частичной суммы, чтобы получить в пределах 1% от полной суммы a${\displaystyle \lceil \rceil }$/ (1 - г ).

Если общее отношение находится в диапазоне -1 < r <0, то геометрический ряд является чередующимся рядом, но может быть преобразован в форму не чередующегося геометрического ряда путем объединения пар членов и последующего анализа скорости сходимости с использованием тот же подход, который показан для диапазона общего отношения 0 < r <1. В частности, частичная сумма

s = a + ar + ar ² + ar ³ + ar ⁴ + ar ⁵ + ... + ar ^n-1 + ar ⁿ в диапазоне -1 < r <0 эквивалентно

s = a - ap + ap ² - ap ³ + ap ⁴ - ap ⁵ + ... + ap ^n-1 - ap ⁿ с нечетным n, с заменой p = - r и в пределах 0 < p <1,

s = ( a - ap ) + ( ap ² - ap ³ ) + ( ap ⁴ - ap ⁵ ) + ... + ( ap ^n-1 - ap ⁿ ) со смежными терминами с разными знаками, соединенными вместе,

s = a (1 - p ) + a (1 - p ) p ² + a (1 - p ) p ⁴ + ... + a (1 - p ) p ^{2 (n-1) / 2} с a (1 - р ) за вычетом каждого члена,

s = a (1 - p ) + a (1 - p ) p ² + a (1 - p ) p ⁴ + ... + a (1 - p ) p ^2m с заменой m = (n - 1) / 2, которое является целым числом с учетом ограничения n нечетным,

которая теперь представлена ​​в виде первых m членов геометрического ряда с коэффициентом a (1 - p ) и знаменателем p ² . Следовательно, замкнутая форма частичной суммы - это (1 - p ) (1 - p ^{2 (m + 1)} ) / (1 - p ² ), которое увеличивается с каждым добавленным членом и в конечном итоге попадает в некоторую небольшую ошибку, E , соотношение полной суммы a (1 - p ) / (1 - p ² ). Как и раньше, решая m на этом пороге ошибки,

${\displaystyle {\begin{aligned}a(1-p)\left({\frac {1-p^{2m+2}}{1-p^{2}}}\right)&\geq a(1-p)\left({\frac {1-E}{1-p^{2}}}\right),\\1-p^{2m+2}&\geq 1-E,\\p^{2m+2}&\leq E,\\ln(p^{2m+2})&\geq ln(E),\\(2m+2)ln(p)&\geq ln(E),\\m+1&\geq \left\lceil {\frac {ln(E)}{2ln(p)}}\right\rceil ,\\m+1&\geq \left\lceil {\frac {ln(E)}{2ln(-r)}}\right\rceil ,\end{aligned}}}$

где 0 < р <1 или , что эквивалентно -1 < г <0, а т + 1 результат является число частичных сумм пар терминов , необходимых для получения в течение более (1 - р ) E / (1 - р ² ) из полная сумма a (1 - p ) / (1 - p ² ). Например, чтобы получить в пределах 1% от полной суммы a (1 - p ) / (1 - p ² ) при p = 0,1 или, что эквивалентно, r = -0,1, только 1 (= ln (E) / (2 ln (p) ) = ln (0,01) / (2 ln (0,1)) требуется пара членов частичной суммы. Однако при p = 0,9 или эквивалентномr = -0.9, 22 (= ln (0.01) / (2 ln (0.9))) пары членов частичной суммы необходимы, чтобы получить в пределах 1% от полной суммы a (1 - p ) / (1 - p ² ). При сравнении скорости сходимости для положительных и отрицательных значений r , n + 1 (количество членов, необходимое для достижения порога ошибки для некоторого положительного r ) всегда вдвое больше, чем m + 1 (количество пар терминов, необходимых для достижения порог ошибки для отрицательного значения r ), но m + 1 относится к парам терминов, а не к отдельным элементам. Таким образом, скорость сходимости симметрична относительно г = 0, который может быть неожиданностью данной асимметрии а/ (1 - г ). Одна точка зрения, которая помогает объяснить эту симметрию скорости сходимости, заключается в том, что на стороне r > 0 каждый добавленный член частичной суммы вносит конечный вклад в бесконечную сумму при r = 1, в то время как на стороне r <0 каждый добавленный член дает конечный вклад в бесконечный наклон при r = -1.

Кроме того, этот тип анализа скорости сходимости особенно полезен при вычислении количества членов ряда Тейлора, необходимых для адекватной аппроксимации некоторой выбранной пользователем достаточно гладкой функции, или при вычислении числа членов ряда Фурье, необходимых для адекватной аппроксимации некоторой пользовательской функции. выбранная периодическая функция.

Исторические сведения [ править ]

Евклид [ править ]

Книга IX, предложение 35 ^[6] из Евклида элементов выражает частичную сумму геометрической прогрессии с точки зрения членов ряда. Это эквивалент современной формулы.

Квадратура параболы Архимеда [ править ]

Архимед использовал сумму геометрического ряда, чтобы вычислить площадь, ограниченную параболой и прямой линией. Его метод заключался в том, чтобы разрезать область на бесконечное количество треугольников.

Теорема Архимеда утверждает, что общая площадь под параболой составляет 4/3 площади синего треугольника.

Архимед определил, что каждый зеленый треугольник имеет 1/8 площади синего треугольника, каждый желтый треугольник имеет 1/8 площади зеленого треугольника и так далее.

Предполагая, что синий треугольник имеет площадь 1, общая площадь представляет собой бесконечную сумму:

${\displaystyle 1\,+\,2\left({\frac {1}{8}}\right)\,+\,4\left({\frac {1}{8}}\right)^{2}\,+\,8\left({\frac {1}{8}}\right)^{3}\,+\,\cdots .}$

Первый член представляет площадь синего треугольника, второй член - площади двух зеленых треугольников, третий член - площади четырех желтых треугольников и т. Д. Упрощение дробей дает

${\displaystyle 1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .}$

Это геометрический ряд с знаменателем 1/4, а дробная часть равна

${\displaystyle \sum _{n=0}^{\infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+\cdots ={4 \over 3}.}$

Сумма

${\displaystyle {\frac {1}{1-r}}\;=\;{\frac {1}{1-{\frac {1}{4}}}}\;=\;{\frac {4}{3}}.}$

Это вычисление использует метод исчерпания , раннюю версию интеграции . Используя исчисление , ту же площадь можно найти с помощью определенного интеграла .

Приложения [ править ]

Повторяющиеся десятичные дроби [ править ]

Повторяющуюся десятичную дробь можно представить себе как геометрический ряд, общее отношение которого равно степени 1/10. Например:

${\displaystyle 0.7777\ldots \;=\;{\frac {7}{10}}\,+\,{\frac {7}{100}}\,+\,{\frac {7}{1000}}\,+\,{\frac {7}{10000}}\,+\,\cdots .}$

Формулу суммы геометрического ряда можно использовать для преобразования десятичной дроби в дробь,

${\displaystyle 0.7777\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {7/10}{1-1/10}}\;=\;{\frac {7/10}{9/10}}\;=\;{\frac {7}{9}}.}$

Формула работает не только для одной повторяющейся фигуры, но и для повторяющейся группы фигур. Например:

${\displaystyle 0.123412341234\ldots \;=\;{\frac {a}{1-r}}\;=\;{\frac {1234/10000}{1-1/10000}}\;=\;{\frac {1234/10000}{9999/10000}}\;=\;{\frac {1234}{9999}}.}$

Обратите внимание, что каждую серию повторяющихся последовательных десятичных знаков можно удобно упростить следующим образом:

${\displaystyle 0.09090909\ldots \;=\;{\frac {09}{99}}\;=\;{\frac {1}{11}}.}$

${\displaystyle 0.143814381438\ldots \;=\;{\frac {1438}{9999}}.}$

${\displaystyle 0.9999\ldots \;=\;{\frac {9}{9}}\;=\;1.}$

То есть повторяющаяся десятичная дробь с повторяющейся длиной n равна частному повторяющейся части (как целое число) и 10 ⁿ - 1 .

Экономика [ править ]

В экономике , геометрические серии используются для представления текущей стоимости в качестве аннуитета (денежную сумму, подлежащую выплате в регулярные промежутки времени).

Например, предположим, что владельцу аннуитета будет выплачиваться 100 долларов один раз в год (в конце года) бессрочно . Получение 100 долларов через год будет стоить меньше, чем сразу 100 долларов, потому что нельзя вкладывать деньги, пока не получишь. В частности, приведенная стоимость 100 долларов через год в будущем составляет 100 долларов / (1 +  ), где - годовая процентная ставка.${\displaystyle I}$${\displaystyle I}$

Аналогичным образом, платеж в размере 100 долларов через два года в будущем имеет приведенную стоимость 100 долларов / (1 +  ) ² (в квадрате, потому что двухлетние проценты теряются из-за того, что деньги не поступят прямо сейчас). Следовательно, приведенная стоимость получения 100 долларов в год бессрочно составляет${\displaystyle I}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {\$100}{(1+I)^{n}}},}$

что представляет собой бесконечную серию:

${\displaystyle {\frac {\$100}{(1+I)}}\,+\,{\frac {\$100}{(1+I)^{2}}}\,+\,{\frac {\$100}{(1+I)^{3}}}\,+\,{\frac {\$100}{(1+I)^{4}}}\,+\,\cdots .}$

Это геометрический ряд со знаменателем 1 / (1 +  ). Сумма - это первое слагаемое, деленное на (единица минус обычное отношение):${\displaystyle I}$

${\displaystyle {\frac {\$100/(1+I)}{1-1/(1+I)}}\;=\;{\frac {\$100}{I}}.}$

Например, если годовая процентная ставка составляет 10% (  = 0,10), то вся рента имеет приведенную стоимость 100 долларов США / 0,10 = 1000 долларов США.${\displaystyle I}$

Такой вид расчетов используется для расчета годовой процентной ставки ссуды (например, ипотечной ссуды ). Она также может быть использована для оценки текущей стоимости ожидаемых фондовых дивидендов , или конечной стоимости в виде безопасности .

Фрактальная геометрия [ править ]

В исследовании фракталов , геометрические ряды часто возникают в периметре , площади или объема в виде автомодельного фигуры.

Например, область внутри снежинки Коха можно описать как объединение бесконечного множества равносторонних треугольников (см. Рисунок). Каждая сторона зеленого треугольника составляет ровно 1/3 размера стороны большого синего треугольника и, следовательно, имеет ровно 1/9 площади. Точно так же каждый желтый треугольник имеет 1/9 площади зеленого треугольника и так далее. Принимая синий треугольник за единицу площади, общая площадь снежинки равна

${\displaystyle 1\,+\,3\left({\frac {1}{9}}\right)\,+\,12\left({\frac {1}{9}}\right)^{2}\,+\,48\left({\frac {1}{9}}\right)^{3}\,+\,\cdots .}$

Первый член этого ряда представляет площадь синего треугольника, второй член - общую площадь трех зеленых треугольников, третий член - общую площадь двенадцати желтых треугольников и так далее. За исключением начальной 1, этот ряд является геометрическим с постоянным соотношением r  = 4/9. Первый член геометрического ряда равен a  = 3 (1/9) = 1/3, поэтому сумма равна

${\displaystyle 1\,+\,{\frac {a}{1-r}}\;=\;1\,+\,{\frac {\frac {1}{3}}{1-{\frac {4}{9}}}}\;=\;{\frac {8}{5}}.}$

Таким образом, снежинка Коха занимает 8/5 площади основного треугольника.

Парадоксы Зенона [ править ]

Сходимость геометрической прогрессии показывает , что сумма с участием бесконечного числа слагаемых действительно может быть конечной, и поэтому позволяет решить многий Зенон парадоксы «s. Например, парадокс дихотомии Зенона утверждает, что движение невозможно, поскольку любой конечный путь можно разделить на бесконечное количество шагов, при этом каждый шаг равен половине оставшегося расстояния. Ошибка Зенона заключается в предположении, что сумма бесконечного числа конечных шагов не может быть конечной. Это, конечно, не так, о чем свидетельствует сходимость геометрического ряда с .${\displaystyle r=1/2}$

Это, однако, не является полным разрешением парадокса дихотомии Зенона. Строго говоря, если мы не допустим обратного движения времени, когда размер шага начинается с и приближается к нулю в качестве предела, эта бесконечная серия в противном случае должна была бы начинаться с бесконечно малого шага. Такое рассмотрение бесконечно малых величин обычно не является чем-то, что строго определяется математически, помимо нестандартного исчисления . Итак, хотя верно то, что все бесконечное суммирование дает конечное число, мы не можем создать простой порядок членов, начиная с бесконечно малого, и поэтому мы не можем адекватно описать первый шаг любого данного действия.${\displaystyle r=1/2}$

Геометрический степенной ряд [ править ]

Формула геометрического ряда

${\displaystyle {\frac {1}{1-x}}=1+x+x^{2}+x^{3}+x^{4}+\cdots }$

можно интерпретировать как степенной ряд в смысле теоремы Тейлора , сходящийся где . Отсюда можно экстраполировать и получить другой степенной ряд. Например,${\displaystyle |x|<1}$

${\displaystyle {\begin{aligned}\tan ^{-1}(x)&=\int {\frac {dx}{1+x^{2}}}\\&=\int {\frac {dx}{1-(-x^{2})}}\\&=\int \left(1+\left(-x^{2}\right)+\left(-x^{2}\right)^{2}+\left(-x^{2}\right)^{3}+\cdots \right)dx\\&=\int \left(1-x^{2}+x^{4}-x^{6}+\cdots \right)dx\\&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}.\end{aligned}}}$

Дифференцируя геометрический ряд, получаем вариант ^[7]

${\displaystyle \sum _{n=1}^{\infty }nx^{n-1}={\frac {1}{(1-x)^{2}}}\quad {\text{ for }}|x|<1.}$

Аналогичным образом получаются:

${\displaystyle \sum _{n=2}^{\infty }n(n-1)x^{n-2}={\frac {2}{(1-x)^{3}}}\quad {\text{ for }}|x|<1,}$ и

${\displaystyle \sum _{n=3}^{\infty }n(n-1)(n-2)x^{n-3}={\frac {6}{(1-x)^{4}}}\quad {\text{ for }}|x|<1.}$

См. Также [ править ]

• 0,999 ...  - Альтернативное десятичное разложение числа 1
• Асимптота  - в геометрии предел касательной в точке, стремящейся к бесконечности.
• Расходящиеся геометрические серии
• Обобщенная гипергеометрическая функция
• Геометрическая прогрессия
• Серия Неймана
• Соотношение тест
• Корневой тест
• Серия (математика)  - Бесконечная сумма

Определенная геометрическая серия [ править ]

• Серия Гранди : 1 - 1 + 1 - 1 + ⋯
• 1 + 2 + 4 + 8 + ⋯
• 1–2 + 4–8 + ⋯
• 1/2 + 1/4 + 1/8 + 1/16 + ⋯
• 1/2 - 1/4 + 1/8 - 1/16 + ⋯
• 1/4 + 1/16 + 1/64 + 1/256 + ⋯
• Геометрический ряд является единичным рядом (сумма ряда сходится к единице) тогда и только тогда, когда | г | <1 и a + r = 1 (эквивалент более знакомой формы S = a / (1 - r ) = 1, когда | r | <1). Следовательно, чередующийся ряд также является единичным рядом, когда -1 < r <0 и a + r = 1 (например, коэффициент a = 1,7 и знаменатель r = -0,7).
• Члены геометрического ряда также являются членами обобщенной последовательности Фибоначчи (F _n = F _n-1 + F _n-2, но без требования F ₀ = 0 и F ₁ = 1), когда коэффициент отношения геометрического ряда r удовлетворяет условию ограничение 1 + r = r ² , которое в соответствии с формулой корней квадратного уравнения имеет место, когда коэффициент отношения r равен золотому сечению (т.е. коэффициент отношения r = (1 ± √5) / 2).
• Единственный геометрические серии , что представляет собой серию блока , а также имеют условие обобщенной последовательности Фибоначчи имеет золотое сечение в качестве коэффициента а и конъюгат золотого сечение , как его общего отношение г (то есть, а = (1 + √5) / 2 и г = (1 - √5) / 2). Это единичная серия, потому что a + r = 1 и | г | <1, это обобщенная последовательность Фибоначчи, потому что 1 + r = r ² , и это переменная серия, потому что r <0.

Примечания [ править ]

Ссылки [ править ]

Внешние ссылки [ править ]

• "Геометрическая прогрессия" , Энциклопедия математики , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. "Геометрические ряды" . MathWorld .
• Геометрические ряды в PlanetMath .
• Пеппард, Ким. "Учебник по алгебре геометрических последовательностей и рядов в колледже" . Западный Техасский университет A&M.
• Кассельман, Билл. «Геометрическая интерпретация геометрического ряда» . Архивировано из оригинального (апплета) 29 сентября 2007 года.
• «Геометрическая серия» Михаэля Шрайбера, Демонстрационный проект Вольфрама , 2007.