Из Википедии, бесплатной энциклопедии
Перейти к навигации Перейти к поиску
Граф Гершеля
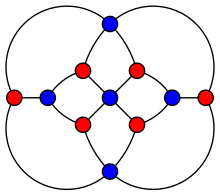Граф Гершеля LS.svg
Граф Гершеля.
Названный в честьАлександр Стюарт Гершель
Вершины11
Края18
Радиус3
Диаметр4
Обхват4
Автоморфизмы12 ( D 6 )
Хроматическое число2
Хроматический индекс4
ХарактеристикиМногогранный
плоский
двудольный
совершенный
Таблица графиков и параметров

В теории графов , ветвь математики , то граф Гершель является двудольный неориентированный граф с 11 вершинами и 18 ребрами, наименьший негамильтонова многогранной графа. Он назван в честь британского астронома Александра Стюарта Гершеля .

Свойства [ править ]

Граф Гершеля является плоским графом : его можно нарисовать на плоскости так, чтобы ни одно из его ребер не пересекалось. Он также является 3-вершинно-связным : удаление любых двух его вершин оставляет связный подграф . Это двудольный граф : его вершины можно разделить на два подмножества по пять и шесть вершин соответственно, так что каждое ребро имеет конечную точку в каждом подмножестве (красный и синий подмножества на рисунке). Как и любой двудольный граф, граф Гершеля является совершенным графом  : хроматическое число каждого индуцированного подграфа равно размеру наибольшей клики этого подграфа. Имеет также хроматический индекс 4, обхват 4, радиус 3 и диаметр 4.

Многогранник [ править ]

Граф Гершеля как многогранник. [1] Щелкните здесь, чтобы просмотреть анимированную версию .

Граф Гершеля плоский и 3-вершинно-связный, поэтому по теореме Стейница следует, что это многогранный граф : существует выпуклый многогранник ( эннеэдр ), имеющий граф Гершеля в качестве скелета . [2] Этот многогранник имеет девять четырехугольников для граней, из которых можно образовать три ромба и шесть воздушных змеев . [1]

Его двойственный многогранник представляет собой выпрямленную треугольную призму, образованную как выпуклая оболочка из середин граней треугольной призмы . Этот многогранник обладает тем свойством, что его грани не могут быть пронумерованы таким образом, чтобы последовательные числа появлялись на смежных гранях, и чтобы первое и последнее число также находились на смежных гранях. Поскольку многогранная нумерация граней этого типа используется в качестве «счетчиков жизни» в игре Magic: The Gathering , Константинидес и Константинидес (2018) называют каноническую многогранную реализацию этого двойного многогранника «Немезидой Лича». [3]

Гамильтоничность [ править ]

Гамильтонов путь (но не цикл) в графе Гершеля

Как двудольный граф с нечетным числом вершин, граф Гершеля не содержит гамильтонова цикла (цикла ребер, проходящего через каждую вершину ровно один раз). Ведь в любом двудольном графе любой цикл должен чередоваться между вершинами по обе стороны от двудольного графа и, следовательно, должен содержать равное количество вершин обоих типов и иметь четную длину. Таким образом, цикл, проходящий один раз через каждую из одиннадцати вершин, не может существовать в графе Гершеля. Это наименьший негамильтонов многогранный граф, независимо от того, измеряется ли размер графа числом его вершин, ребер или граней. [4] Существуют и другие многогранные графы с 11 вершинами и без гамильтоновых циклов (особенно граф Голднера – Харари [5]), но с меньшим количеством граней. [2]

Все вершины графа Гершеля, кроме трех, имеют степень три. Гипотеза Тейта [6] утверждает, что многогранный граф, в котором каждая вершина имеет степень три, должен быть гамильтоновым, но это было опровергнуто, когда У. Т. Тутте предоставил контрпример, гораздо больший граф Тутте . [7] Уточнение гипотезы Тэта, гипотезы Барнетта о том, что каждый двудольный 3-регулярный многогранный граф является гамильтоновым, остается открытым. [8]

Каждый максимальный планарный граф , не имеющий гамильтонова цикла, имеет граф Гершеля как минор . Предполагается, что граф Гершеля является одним из трех минорно-минимальных негамильтоновых 3-вершинно-связных графов. Два других - это полный двудольный граф и граф, образованный разделением графа Гершеля и на две симметричные половины разделителями с тремя вершинами и последующим объединением одной половины из каждого графа. [9]

Медиальный график графа Гершель является 4-регулярный плоский граф , без гамильтонова разложения . Заштрихованные области соответствуют вершинам нижележащего графа Гершеля.

Граф Гершеля также представляет собой пример многогранного графа, для которого средний граф не может быть разложен на два гамильтоновых цикла с непересекающимися ребрами. Медиальный граф графа Гершеля - это 4- регулярный граф с 18 вершинами, по одной на каждое ребро графа Гершеля; две вершины смежны в медиальном графе, если соответствующие ребра графа Гершеля идут подряд на одной из его граней. [10] Это 4-вершинно-связное и по существу 6-реберное связное , что означает, что для каждого разбиения вершин на два подмножества, по крайней мере, из двух вершин, есть не менее шести ребер, пересекающих разбиение. [11]

История [ править ]

Гершель граф назван в честь британского астронома Александра Стюарт Гершеля , который писал ранний документ , касающийся Уильям Роуэн Гамильтон «s icosian game : граф Гершель описывает наименьший выпуклый многогранник , для которого эта игра не имеет решения. Однако в статье Гершеля решения для икозианской игры описаны только на графах правильного тетраэдра и правильного икосаэдра ; он не описывал граф Гершеля. [12] Название «граф Гершеля» впервые появилось в учебнике теории графов Джона Адриана Бонди и USR Murty , опубликованном в 1976 г. [13]Однако сам график был описан ранее, например, HSM Coxeter . [2]

Ссылки [ править ]

  1. ^ a b Lawson-Perfect, Christian (13 октября 2013 г.), «Эннеэдр для Гершеля» , The Aperiodical , извлечено 7 декабря 2016 г.
  2. ^ a b c Coxeter, HSM (1973), Regular Polytopes , Dover, p. 8 CS1 maint: обескураженный параметр ( ссылка ).
  3. ^ Константинидес, Энтони Ф .; Constantinides, Джордж А. (октябрь 2018), "Spindown многогранники", Математическая газета , 102 (555): 447-453, DOI : 10,1017 / mag.2018.111
  4. ^ Барнетт, Дэвид; Юкович, Эрнест (1970), «Гамильтоновы схемы на 3-многогранниках», Журнал комбинаторной теории , 9 (1): 54–59, DOI : 10.1016 / S0021-9800 (70) 80054-0.
  5. ↑ Weisstein, Eric W. , "Goldner-Harary Graph" , MathWorld.
  6. ↑ Tait, PG (1884), « Топология листинга » , Philosophical Magazine , 5-я серия, 17 : 30–46 CS1 maint: discouraged parameter (link). Перепечатано в Scientific Papers , Vol. II, стр. 85–98.
  7. ^ Tutte, WT (1946), "О гамильтоновых схемах" (PDF) , Журнал Лондонского математического общества , 21 (2): 98–101, DOI : 10.1112 / jlms / s1-21.2.98 CS1 maint: discouraged parameter (link).
  8. ↑ Samal, Роберт (11 июня 2007 г.), гипотеза Барнетта , Open Problem Garden , извлечено 24 февраля 2011 г. CS1 maint: discouraged parameter (link)
  9. ^ Дин, Гуоли; Маршалл, Эмили (2018), "Минимальные -связные негамильтоновы графы", графы и комбинаторика , 34 (2): 289-312, DOI : 10.1007 / s00373-018-1874-г , МР 3774453 
  10. ^ Бонди, JA; Häggkvist, R. (1981), "Край-непересекающиеся Гамильтон циклы в 4-регулярных плоских графов", Aequationes Mathematicae , 22 (1): 42-45, DOI : 10.1007 / BF02190157.
  11. ^ Кирали, Чаба; Péterfalvi, Ференц (2012), "Сбалансированные общие схемы без длинных путей", дискретная математика , 312 (15): 2262-2271, DOI : 10.1016 / j.disc.2012.03.031 , МР 2926099 
  12. ↑ Herschel, AS (1862), «Икосианская игра сэра У. Гамильтона» , Ежеквартальный журнал чистой и прикладной математики , 5 : 305 CS1 maint: discouraged parameter (link).
  13. ^ Бонди, JA ; Мурти, USR (1976), Теория графов с приложениями , Северная Голландия, стр. 53, Руководство MR 0411988 

Внешние ссылки [ править ]

  • Вайсштейн, Эрик В. , «График Гершеля» , MathWorld