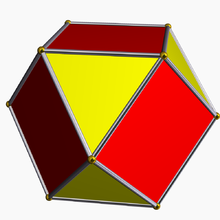

В евклидовой геометрии , ректификации , также известная как критическое усечение или полные-усечения это процесс усечения многогранника , пометив средние точки всех его ребер, и отрезав его вершину в этих точках. [1] Результирующий многогранник будет ограничен фасетами вершинной фигуры и выпрямленными фасетами исходного многогранника.
Оператор исправления иногда обозначается буквой r с символом Шлефли . Например, r {4,3} - это выпрямленный куб , также называемый кубооктаэдром и также представленный как . И выпрямленный кубооктаэдр rr {4,3} - это ромбокубооктаэдр , который также обозначается как .
Конвое полиэдр обозначение использует для амвона в качестве этого оператора. В теории графов эта операция создает средний граф .
Исправление любого правильного самодвойственного многогранника или мозаики приведет к другому правильному многограннику или мозаике с порядком мозаики 4, например, тетраэдр {3,3} станет октаэдром {3,4}. В качестве особого случая квадратная мозаика {4,4} превратится в другую квадратную мозаику {4,4} при операции исправления.
Пример исправления как окончательного усечения до края [ править ]
Исправление - это последняя точка процесса усечения. Например, на кубе эта последовательность показывает четыре шага континуума усечений между регулярной и исправленной формой:
Исправления высшей степени [ править ]
Выпрямление более высокой степени может быть выполнено на регулярных многогранниках более высокой размерности. Наивысшая степень выпрямления создает двойственный многогранник . При исправлении края обрезаются до точек. Биректификация обрезает грани до точек. При триректификации ячейки усекаются до точек и т. Д.
Пример биректификации как окончательного усечения лица [ править ]
Эта последовательность показывает двунаправленный куб как финальную последовательность от куба к двойному, где исходные грани усечены до единственной точки:
В полигонах [ править ]
Двойник многоугольника - это то же самое, что и его выпрямленная форма. Новые вершины помещаются в центр краев исходного многоугольника.
В многогранниках и плоских мозаиках [ править ]
Каждое платоново тело и двойственное к нему имеют один и тот же выпрямленный многогранник. (Это не относится к многогранникам в более высоких измерениях.)
Выпрямленный многогранник оказывается выраженным как пересечение исходного платонового тела с соответствующей масштабной концентрической версией его двойственного. По этой причине его название представляет собой комбинацию имен оригинала и двойника:
- Выпрямленный тетраэдр , двойственный которому является тетраэдр, - это тетраэтраэдр , более известный как октаэдр .
- Выпрямленный октаэдр , двойственный кубу , есть кубооктаэдр .
- Выпрямленный икосаэдр , двойник которого - додекаэдр , есть икосододекаэдр .
- Выпрямленная квадратная плитка - это квадратная плитка .
- Выпрямленная треугольная мозаика или шестиугольная мозаика - это трехгексагональная мозаика .
Примеры
| Семья | Родитель | Исправление | Двойной |
|---|---|---|---|
[p, q] | |||
| [3,3] | Тетраэдр | Октаэдр | Тетраэдр |
| [4,3] | Куб | Кубооктаэдр | Октаэдр |
| [5,3] | Додекаэдр | Икосидодекаэдр | Икосаэдр |
| [6,3] | Шестиугольная черепица | Трехгранная черепица | Треугольная черепица |
| [7,3] | Орден-3 семиугольная черепица | Тригептагональная черепица | Треугольная черепица Order-7 |
| [4,4] | Квадратная плитка | Квадратная плитка | Квадратная плитка |
| [5,4] | Пятиугольная черепица Order-4 | Тетрапентагональная черепица | Квадратная черепица Order-5 |
В нерегулярных многогранниках [ править ]
Если многогранник не правильный, средние точки ребер, окружающие вершину, могут не быть компланарными. Однако в этом случае все еще возможна форма исправления: каждый многогранник имеет многогранный граф в качестве 1-скелета , и из этого графа можно сформировать медиальный граф , поместив вершину в среднюю точку каждого ребра исходного графа и соединив две из этих новых вершин ребром, если они принадлежат последовательным ребрам на общей грани. Полученный медиальный граф остается многогранным, поэтому по теореме Стейница его можно представить в виде многогранника.
Конвей полиэдр обозначения эквивалентна ректификации является AMBO , представленное . Применение дважды aa (исправление исправления) - это операция расширения Конвея , e , которая аналогична операции раскоса Джонсона , t 0,2, созданной из правильных многогранников и мозаик.
В 4-многогранниках и трехмерных сотовых мозаиках [ править ]
Каждый Выпуклый правильный 4-многогранник имеет выпрямленную форму как равномерный 4-многогранник .
В правильном 4-многограннике {p, q, r} есть клетки {p, q}. Его выпрямление будет иметь два типа ячеек: выпрямленный многогранник {p, q}, оставшийся от исходных ячеек, и многогранник {q, r} в виде новых ячеек, образованных каждой усеченной вершиной.
Однако выпрямленный {p, q, r} не то же самое, что выпрямленный {r, q, p}. Дальнейшее усечение, называемое усечением битов , является симметричным между 4-многогранником и двойственным ему. См. Унифицированный 4-многогранник # Геометрические производные .
Примеры
| Семья | Родитель | Исправление | Биректификация (двойное выпрямление) | Триректификация (двойная) |
|---|---|---|---|---|
[ p , q , r ] | { p , q , r } | г { р , д , г } | 2r { p , q , r } | 3r { p , q , r } |
| [3,3,3] | 5-элементный | выпрямленный 5-элементный | выпрямленный 5-элементный | 5-элементный |
| [4,3,3] | тессеракт | исправленный тессеракт | Выпрямленный 16-элементный ( 24-элементный ) | 16 ячеек |
| [3,4,3] | 24-элементный | выпрямленный 24-элементный | выпрямленный 24-элементный | 24-элементный |
| [5,3,3] | 120 ячеек | выпрямленный 120-элементный | выпрямленный 600-элементный | 600 ячеек |
| [4,3,4] | Кубические соты | Ректифицированные соты кубической формы | Ректифицированные соты кубической формы | Кубические соты |
| [5,3,4] | Орден-4 додекаэдр | Выпрямленный додекаэдр порядка 4 | Ректифицированный заказ-5 куб. | Порядка-5 куб. |
Степени исправления [ править ]
Первое исправление обрезает края до точек. Если многогранник является регулярным , эта форма представлена расширенной символ шлефли обозначения т 1 {р, д, ...} или г {р, д, ...}.
Вторая ректификация или birectification , усекает обращена вниз к точкам. Если он обычный, то он имеет обозначение t 2 {p, q, ...} или 2 r {p, q, ...}. Для многогранников двунаправленная ориентация создает двойственный многогранник .
Выпрямления более высокой степени могут быть построены для многогранников более высокой размерности. В общем случае n-исправление обрезает n-грани до точек.
Если n-многогранник (n-1) -исправлен, его фасеты сводятся к точкам, а многогранник становится его двойственным .
Обозначения и аспекты [ править ]
Для каждой степени исправления существуют разные эквивалентные обозначения. В этих таблицах показаны имена по размерам и два типа фасетов для каждого.
Правильные многоугольники [ править ]
Фасеты - это ребра, представленные как {2}.
| имя {p} | Диаграмма Кокстера | t-обозначение символ Шлефли | Вертикальный символ Шлефли | ||
|---|---|---|---|---|---|
| Имя | Фасет-1 | Фасетка-2 | |||
| Родитель | т 0 {p} | {п} | {2} | ||
| Исправленный | т 1 {p} | {п} | {2} | ||
Правильные многогранники и мозаики [ править ]
Грани - это правильные многоугольники.
| имя {p, q} | Диаграмма Кокстера | t-обозначение символ Шлефли | Вертикальный символ Шлефли | ||
|---|---|---|---|---|---|
| Имя | Фасет-1 | Фасетка-2 | |||
| Родитель | т 0 {p, q} | {p, q} | {п} | ||
| Исправленный | t 1 {p, q} | г {р, q} = | {п} | {q} | |
| Биректифицированный | t 2 {p, q} | {q, p} | {q} | ||
Регулярные однородные 4-многогранники и соты [ править ]
Грани - правильные или выпрямленные многогранники.
| имя {p, q, r} | Диаграмма Кокстера | t-обозначение символ Шлефли | Расширенный символ Шлефли | ||
|---|---|---|---|---|---|
| Имя | Фасет-1 | Фасетка-2 | |||
| Родитель | t 0 {p, q, r} | {p, q, r} | {p, q} | ||
| Исправленный | t 1 {p, q, r} | = г {р, д, г} | = г {р, q} | {q, r} | |
| Двунаправленный (Двойное выпрямление) | t 2 {p, q, r} | = г {г, д, р} | {q, r} | = г {д, г} | |
| Триректифицированный (двойной) | t 3 {p, q, r} | {г, д, р} | {г, д} | ||
Правильные 5-многогранники и 4-пространственные соты [ править ]
Грани - это правильные или выпрямленные 4-многогранники.
| имя {p, q, r, s} | Диаграмма Кокстера | t-обозначение символ Шлефли | Расширенный символ Шлефли | ||
|---|---|---|---|---|---|
| Имя | Фасет-1 | Фасетка-2 | |||
| Родитель | t 0 {p, q, r, s} | {p, q, r, s} | {p, q, r} | ||
| Исправленный | t 1 {p, q, r, s} | = r {p, q, r, s} | = г {р, д, г} | {q, r, s} | |
| Биректифицированный (двудиректифицированный двойной) | t 2 {p, q, r, s} | = 2r {p, q, r, s} | = г {г, д, р} | = r {q, r, s} | |
| Триректифицированный (выпрямленный двойной) | t 3 {p, q, r, s} | = r {s, r, q, p} | {г, д, р} | = r {s, r, q} | |
| Квадриректифицированный (двойной) | t 4 {p, q, r, s} | {s, r, q, p} | {s, r, q} | ||
См. Также [ править ]
- Двойной многогранник
- Квазирегулярный многогранник
- Список правильных многогранников
- Усечение (геометрия)
- Обозначения многогранника Конвея
Ссылки [ править ]
- ^ Вайсштейн, Эрик В. «Исправление» . MathWorld .
- Coxeter, HSM Regular Polytopes , (3-е издание, 1973), Dover edition, ISBN 0-486-61480-8 (стр. 145–154 Глава 8: Усечение)
- Единообразные многогранники Нормана Джонсона , рукопись (1991)
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Джон Х. Конвей , Хайди Берджел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)
Внешние ссылки [ править ]
- Ольшевский, Георгий. «Ректификация» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
| Семя | Усечение | Исправление | Bitruncation | Двойной | Расширение | Омнитуркация | Чередования | ||
|---|---|---|---|---|---|---|---|---|---|
| т 0 {p, q} {p, q} | t 01 {p, q} t {p, q} | т 1 {p, q} r {p, q} | t 12 {p, q} 2t {p, q} | t 2 {p, q} 2r {p, q} | t 02 {p, q} rr {p, q} | t 012 {p, q} tr {p, q} | ht 0 {p, q} h {q, p} | ht 12 {p, q} s {q, p} | ht 012 {p, q} sr {p, q} |












