| Кубооктаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Однородный многогранник |
| Элементы | F = 14, E = 24, V = 12 (χ = 2) |
| Лица по сторонам | 8 {3} +6 {4} |
| Обозначение Конвея | аС AAT |
| Символы Шлефли | r {4,3} или rr {3,3} или |
| т 1 {4,3} или т 0,2 {3,3} | |
| Символ Wythoff | 2 | 3 4 3 3 | 2 |
| Диаграмма Кокстера | |
| Группа симметрии | O h , B 3 , [4,3], (* 432), порядок 48 T d , [3,3], (* 332), порядок 24 |
| Группа вращения | O , [4,3] + , (432), порядок 24 |
| Двугранный угол | 125,26 ° угловой секунды (- √ 3 ) |
| Рекомендации | U 07 , C 19 , W 11 |
| Характеристики | Полурегулярный выпуклый квазирегулярный |
 Цветные лица | 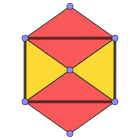 3.4.3.4 ( фигура вершины ) |
 Ромбический додекаэдр ( двойственный многогранник ) |  Сеть |
Кубооктаэдр представляет собой полиэдр с 8 треугольных граней и 6 квадратных граней. Кубооктаэдр имеет 12 одинаковых вершин , по 2 треугольника и 2 квадрата, пересекающихся в каждой, и 24 идентичных ребра , каждое из которых отделяет треугольник от квадрата. Таким образом, это квазирегулярный многогранник , то есть архимедово твердое тело , которое не только вершинно-транзитивно, но и реберно-транзитивно . Это единственный радиально равносторонний выпуклый многогранник.
Его двойственный многогранник - ромбический додекаэдр .
Кубооктаэдр, вероятно, был известен Платону : в « Определениях Герона » цитируется Архимед, говорящий о том, что Платон знал твердое тело, состоящее из 8 треугольников и 6 квадратов. [1]
Другие имена [ править ]
- Гептапараллелоэдр ( Бакминстер Фуллер )
- Фуллер применил к этой форме название « Dymaxion », которое использовалось в ранней версии карты Dymaxion . Он также назвал его «векторным равновесием» из-за его радиальной равносторонней симметрии (радиус от центра до вершины равен длине края). [2] Он назвал кубооктаэдр, состоящий из жестких стоек, соединенных гибкими вершинами, «джиттербагом» (эту форму можно постепенно деформировать в икосаэдр , октаэдр и тетраэдр , свернув его квадратные стороны).
- С симметрией O h порядка 48 это выпрямленный куб или выпрямленный октаэдр ( Норман Джонсон )
- Обладая симметрией T d порядка 24, это угловатый тетраэдр или ромбитратратетраэдр.
- Обладая симметрией D 3d порядка 12, это треугольная гиробикупола .
Площадь и объем [ править ]
Площадь A и объем V кубооктаэдра с длиной ребра a равны:
Ортогональные проекции [ править ]
Кубооктаэдр имеет четыре специальные ортогональные проекции , сосредоточенные на вершине, ребра, и два типа граней, треугольной и площади. Последние два соответствуют самолетам Кокстера B 2 и A 2 . Косые проекции показывают квадрат и шестиугольник, проходящие через центр кубооктаэдра.
| Квадратное лицо | Треугольное лицо | Вершина | Край | Перекос | |
|---|---|---|---|---|---|
| [4] | [6] | [2] | [2] | ||
| Ромбический додекаэдр (Двойной многогранник) | |||||
Сферическая мозаика [ править ]
Кубооктаэдр также можно представить в виде сферической мозаики и спроецировать на плоскость через стереографическую проекцию . Эта проекция является конформной , сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
| орфографическая проекция | квадрат -centered | с центром в треугольнике | Вершина по центру |
|---|---|---|---|
| Стереографическая проекция | |||
Декартовы координаты [ править ]
В декартовы координаты для вершин кубооктаэдр (длины кромки √ 2 ) с центром в начале координат являются:
- (± 1, ± 1,0)
- (± 1,0, ± 1)
- (0, ± 1, ± 1)
Альтернативный набор координат может быть выполнен в 4-м пространстве, как 12 перестановок:
- (0,1,1,2)
Эта конструкция существует как один из 16 ортанте граней в cantellated 16-клетки .
Корневые векторы [ править ]
12 вершин кубооктаэдра могут представлять корневые векторы простой группы Ли A 3 . С добавлением 6 вершин октаэдра эти вершины представляют 18 корневых векторов простой группы Ли B 3 .
Рассечение [ править ]
Кубооктаэдр можно разрезать на две треугольные купола общим шестиугольника , проходящий через центр кубооктаэдра. Если эти два треугольных купола скручены так, что треугольники и квадраты совпадают, образуется твердое тело Джонсона J 27 , треугольная ортобикупола .
Кубооктаэдр также можно разделить на 6 квадратных пирамид и 8 тетраэдров, пересекающихся в центральной точке. Это расслоение выражается в чередующихся кубических сотах, где пары квадратных пирамид объединяются в октаэдры .
Геометрические отношения [ править ]
Симметрии [ править ]
Кубооктаэдр - это уникальный выпуклый многогранник, у которого длинный радиус (от центра до вершины) равен длине ребра; таким образом, его длинный диаметр (от вершины к противоположной вершине) составляет 2 длины ребра. Эта радиальная равносторонняя симметрия является свойством только нескольких однородных многогранников , включая двумерный шестиугольник , трехмерный кубооктаэдр и четырехмерный 24-элементный и 8-элементный (тессеракт) . Радиально равносторонниймногогранники - это такие многогранники, которые могут быть построены с их длинными радиусами из равносторонних треугольников, которые встречаются в центре многогранника, каждый из которых дает два радиуса и ребро. Следовательно, все внутренние элементы, которые встречаются в центре этих многогранников, имеют равносторонний треугольник, обращенный внутрь, как в разрезе кубооктаэдра на 6 квадратных пирамид и 8 тетраэдров. Каждый из этих радиально равносторонних многогранников также встречается как ячейки характерной мозаики, заполняющей пространство : мозаика из правильных шестиугольников, выпрямленных кубических сот (чередующихся кубооктаэдров и октаэдров), сот с 24 ячейками и тессерактических сот , соответственно. Каждая тесселяция имеет двойную тесселяцию.; центры ячеек в тесселяции - это вершины ячеек в двойном тесселяции. Самая плотная из известных регулярных сферических упаковок в двух, трех и четырех измерениях использует центры ячеек одной из этих мозаик в качестве центров сфер.
Кубооктаэдр имеет октаэдрическую симметрию. Его первый плеяде'ученых является соединением из куба и его двойной октаэдр с вершинами кубооктаэдра , расположенным в серединах ребер либо.
Конструкции [ править ]
Кубооктаэдр можно получить, взяв экваториальное поперечное сечение четырехмерного 24- или 16-элементного . Шестиугольник можно получить, взяв экваториальное сечение кубооктаэдра.
Кубооктаэдр - это выпрямленный куб, а также выпрямленный октаэдр .
Это также угловатый тетраэдр . В этой конструкции ему дается символ Wythoff : 3 3 | 2 .
При перекосе тетраэдра образуется твердое тело с гранями, параллельными граням кубооктаэдра, а именно восемь треугольников двух размеров и шесть прямоугольников. Хотя его ребра не равны, это твердое тело остается однородным по вершинам : твердое тело имеет полную тетраэдрическую группу симметрии, и его вершины эквивалентны в этой группе.
Ребра кубооктаэдра образуют четыре правильных шестиугольника . Если кубооктаэдр разрезан в плоскости одного из этих шестиугольников, каждая половина будет треугольным куполом , одним из тел Джонсона ; сам кубооктаэдр, таким образом, также может быть назван треугольной гиробикуполой , простейшим из ряда (кроме gyrobifastigium или «дигональной гиробикуполы»). Если половинки соединить вместе с поворотом так, чтобы треугольники встретились с треугольниками, а квадраты встретились с квадратами, в результате получится еще одно твердое тело Джонсона, треугольная ортобикупола , также называемая антикубоктаэдром.
Оба треугольных бикупола важны для упаковки сфер . Расстояние от центра твердого тела до его вершин равно длине его ребра. Каждая центральная сфера может иметь до двенадцати соседей, и в гранецентрированной кубической решетке они занимают позиции вершин кубооктаэдра. В гексагональной плотноупакованной решетке они соответствуют углам треугольного ортобикупола. В обоих случаях центральная сфера занимает положение центра твердого тела.
Кубооктаэдры появляются как ячейки в трех выпуклых однородных сотах и в девяти выпуклых однородных 4-многогранниках .
Объем кубооктаэдра равен 5/6 окружающего куба и 5/8 окружающего октаэдра.
Расположение вершин [ править ]
Потому что радиально равносторонняя, центр кубооктаэдра можно рассматривать как 13 - каноническую апикальную вершину , одна длины ребра на расстояние от 12 обычных вершин, как вершина из канонической пирамиды является одна длиной ребра на равном расстоянии от других его вершин.
Кубооктаэдр имеет общие ребра и расположение вершин с двумя невыпуклыми однородными многогранниками : кубогемиоктаэдром (имеющим общие квадратные грани) и октагемиоктаэдром (имеющим общие треугольные грани). Он также служит в качестве наклонного тетраэдра , как выпрямленный тетраэдр .
Кубооктаэдр | Кубогемиоктаэдр | Октагемиоктаэдр |
Кубооктаэдр 2-охватывает в тетрагемигексаэдр , [3] , который , соответственно , имеет ту же самую абстрактную вершину фигуры (два треугольника и два квадрата: 3.4.3.4) и половина вершин, ребер и граней. (Фактическая фигура вершины тетрагемигексаэдра равна 3,4.3/2.4, с а/2 фактор из-за креста.)
Кубооктаэдр | Тетрагемигексаэдр |
Связанные многогранники [ править ]
Кубооктаэдр - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия : [4,3], (* 432) | [4,3] + (432) | [1 + , 4,3] = [3,3] (* 332) | [3 + , 4] (3 * 2) | |||||||
| {4,3} | т {4,3} | г {4,3} г {3 1,1 } | т {3,4} т {3 1,1 } | {3,4} {3 1,1 } | rr {4,3} s 2 {3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | ч 2 {4,3} т {3,3} | с {3,4} с {3 1,1 } |
знак равно | знак равно | знак равно | ||||||||
| Двойники к однородным многогранникам | ||||||||||
| V4 3 | V3.8 2 | В (3,4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | V3.6 2 | V3 5 |
Кубооктаэдр также имеет тетраэдрическую симметрию с двумя цветами треугольников.
| Семейство равномерных тетраэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : [3,3] , (* 332) | [3,3] + , (332) | ||||||
| {3,3} | т {3,3} | г {3,3} | т {3,3} | {3,3} | рр {3,3} | tr {3,3} | ср {3,3} |
| Двойники к однородным многогранникам | |||||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Связанные квазирегулярные многогранники и мозаики [ править ]
Кубооктаэдр существует в последовательности симметрий квазирегулярных многогранников и мозаик с конфигурациями вершин (3. n ) 2 , переходящих от мозаик сферы к евклидовой плоскости и в гиперболическую плоскость. С орбифолдной нотацией симметрии * n 32 все эти мозаики являются конструкцией Wythoff в фундаментальной области симметрии с точками образующих в правом углу области. [4] [5]
| * n 32 орбифолдных симметрии квазирегулярных мозаик : (3. n ) 2 | |||||||
|---|---|---|---|---|---|---|---|
Строительство | Сферический | Евклидово | Гиперболический | ||||
| * 332 | * 432 | * 532 | * 632 | * 732 | * 832 ... | * ∞32 | |
| Квазирегулярные фигуры | |||||||
| Вершина | (3,3) 2 | (3,4) 2 | (3,5) 2 | (3,6) 2 | (3,7) 2 | (3.8) 2 | (3.∞) 2 |
| * n 42 изменения симметрии квазирегулярных мозаик: (4. n ) 2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия * 4 n 2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | |||
| * 342 [3,4] | * 442 [4,4] | * 542 [5,4] | * 642 [6,4] | * 742 [7,4] | * 842 [8,4] ... | * ∞42 [∞, 4] | [ n i, 4] | |
| Цифры | ||||||||
| Конфиг. | (4,3) 2 | (4,4) 2 | (4,5) 2 | (4,6) 2 | (4,7) 2 | (4,8) 2 | (4.∞) 2 | (4. n i) 2 |
Этот многогранник топологически связан как часть последовательности скошенных многогранников с фигурой вершины (3.4. N .4) и продолжается как мозаики гиперболической плоскости . Эти вершинно-транзитивные фигуры обладают (* n 32) отражательной симметрией .
| * n 32 изменение симметрии расширенных мозаик: 3.4. п. 4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия * n 32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paracomp. | ||||
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3] ... | * ∞32 [∞, 3] | |
| Фигура | ||||||||
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Связанные многогранники [ править ]
Кубооктаэдр можно разложить на правильный октаэдр и восемь неправильных, но равных октаэдров в форме выпуклой оболочки куба с удаленными двумя противоположными вершинами. Это разложение кубооктаэдра соответствует проекции 24-ячеек, параллельной первой ячейке, на три измерения. Под этой проекцией кубооктаэдр образует оболочку проекции, которую можно разложить на шесть квадратных граней, правильный октаэдр и восемь неправильных октаэдров. Эти элементы соответствуют изображениям шести октаэдрических ячеек в 24-ячейке, ближайшей и самой дальней ячеек с точки зрения 4D и оставшимся восьми парам ячеек, соответственно.
Культурные события [ править ]
- В эпизоде « Звездного пути » « Под любым другим именем » инопланетяне захватывают « Энтерпрайз », превращая членов экипажа в неодушевленные кубооктаэдры.
- Непоседа "Geo Twister" [1] представляет собой гибкий кубооктаэдр.
- Космические станции Кориолиса в серии компьютерных игр Elite имеют форму кубооктаэдра.
- Весак Кууду, традиционные фонари, которые делают в Шри-Ланке ежегодно в честь дня Весак Пойя, обычно имеют кубооктаэдрическую форму.
- «Лунные змеи» из Super Mario Odyssey . [6]
- InfluxData , компания, создающая базу данных временных рядов InfluxDB , использует кубооктаэдр в своем логотипе .
Кубооктаэдрический граф [ править ]
| Кубооктаэдрический граф | |
|---|---|
4-х кратная симметрия | |
| Вершины | 12 |
| Края | 24 |
| Автоморфизмы | 48 |
| Характеристики |
|
| Таблица графиков и параметров | |
В математической области теории графов , A кубооктаэдрические графики являются графиком вершин и ребер из кубооктаэдра, один из Архимеда твердых веществ . Его также можно построить как линейный график куба. Он имеет 12 вершин и 24 ребра, является локально линейным и является архимедовым графом четвертой степени . [7]
6-кратная симметрия |
См. Также [ править ]
- Икосододекаэдр
- Псевдокубооктаэдр
- Ромбокубооктаэдр
- Усеченный кубооктаэдр
- Тетрадекаэдр
Ссылки [ править ]
- ^ Хит, Томас Л. (1931), Руководство по греческой математике , Кларендон, стр. 176
- ^ Векторное равновесие: Р. Бакминстер Фуллер
- ^ Рихтер, Дэвид А., две модели вещественной проективной плоскости , в архиве с оригинала на 2016-03-03 , извлекаться 2010-04-15
- ^ Косетер, HSM (1973), регулярные многогранники (3 - й изд.), Dover, Глава V: Калейдоскоп, Раздел: 5,7 построения визофф в , ISBN 0-486-61480-8
- ^ Двумерные мутации симметрии Дэниел Хьюсон
- ^ "Файл: Moonsnake Icon SMO.png - Super Mario Wiki, энциклопедия Марио" . www.mariowiki.com . Проверено 5 ноября 2018 .
- ^ Читать, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269
Дальнейшее чтение [ править ]
- Гика, Матила (1977). Геометрия искусства и жизни ([Nachdr.] Ed.). Нью-Йорк: Dover Publications . С. 51–56, 81–84 . ISBN 9780486235424.
- Вайсштейн, Эрик В. (2002). «Кубооктаэдр». CRC Краткая энциклопедия математики (2-е изд.). Хобокен: CRC Press . С. 620–621. ISBN 9781420035223.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . ISBN Dover Publications, Inc. 0-486-23729-X. (Раздел 3-9)
- Кромвель, П. Многогранники , CUP hbk (1997), pbk. (1999). Глава 2 с. 79-86 Архимедовы тела
Внешние ссылки [ править ]
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников
- Эрик В. Вайсштейн , Кубооктаэдр ( архимедово твердое тело ) в MathWorld .
- Кубооктаэдр на сайте Hexnet, посвященном математике шестиугольника.
- Клитцинг, Ричард. «Трехмерные выпуклые равномерные многогранники o3x4o - co» .
- Редактируемая печатная сетка кубооктаэдра с интерактивным трехмерным изображением



